PSO-ILS优化WSN节点部署
基于粒子群优化和迭代局部搜索算法的无线传感器网络节点部署优化
摘要
覆盖与连通性是基于目标的无线传感器网络（WSN）中最具挑战性的两个问题。为此，节点部署是影响无线传感器网络覆盖与连通性性能的基本问题之一。本文提出了一种结合粒子群优化与迭代局部搜索（PSO‐ILS）的新方法，旨在以最少数量的节点实现最佳覆盖和连通率。一方面，为保持目标点的全覆盖，采用PSO‐ILS部署最少数量的传感器节点；另一方面，为实现完全连通性，提出了最优位置确定（OPD）算法，用于识别最优候选位置，供PSO‐ILS部署最少数量的中继节点。通过对多次运行结果的比较，本文将所提方法与标准PSO、差分进化（DE）和遗传算法（GA）进行了对比。综合分析结果表明，PSO‐ILS在选择潜在位置以确保目标点的全覆盖以及所需中继节点数量以实现完全连通性方面，相较于PSO、DE和GA方法具有显著的性能提升。
关键词 连通性，覆盖，节点部署，粒子群优化，无线传感器网络
引言
无线传感器网络（WSN）包含一组具有低能量源和有限处理能力的互连设备。它能够随时随地通过不同的传感器对环境进行感知和监测。这些设备相互通信并协作以完成给定的任务。
由于这些设备具有灵活性、低成本和易于部署的特点，无线传感器网络在工业过程、国防与军事监视、家庭自动化、灾害检测与控制、环境监测、医疗与安全以及物流与智能交通等多个领域具有广泛的应用前景。在无线传感器网络中，节点通常能量有限。因此，对传感器能量资源的高效利用以及网络寿命最大化是大多数传感器网络协议提出的主要设计考虑因素。
目标覆盖是无线传感器网络的关键应用。因此，传感器布置是传感器目标覆盖设计中的一个基本问题，它决定了许多关键特性，例如其覆盖范围，连通性、准确性、成本和网络寿命。在这种类型的应用中，要求区域内的每个目标至少被k个不同的节点覆盖。在这种情况下，随机部署并不合适，因为它不一定能保证网络的完全覆盖与连通性。因此，特别是在传感器节点较为昂贵或其位置对其运行有显著影响时，通常采用预规划部署。确定性部署可以最小化部署的节点数量，从而降低整个网络的成本。此外，减少部署的传感器数量还能降低传输到基站（BS）的消息数量，因此可以最小化整体能耗，并延长网络寿命。
然而，在所有部署策略中，确保整个网络的最佳覆盖与连通性都极为关键。
本文中，我们处理目标覆盖问题。我们的首要目标是选择最少数量的潜在位置来部署传感器节点，以确保目标点的k‐覆盖。在k‐覆盖问题中，每个目标点需要被至少k个不同的工作传感器所覆盖。
为了实现节能且可靠的数据传输，许多研究人员设计并开发了不同的路由协议。这些方法的主要目标是通过网络找到最佳路径。最优化的路由取决于路由协议所使用的度量指标，如能量消耗、延迟、成本、交通拥堵以及数据传输的可靠性。然而，在路由算法中，靠近基站的传感器节点需要为其他节点转发数据包。这些节点比其他节点消耗更多的能量，因而容易快速死亡。结果导致监测区域出现覆盖空洞，网络被分割，进而造成网络连通性中断，并在网络中形成能量空洞。为了减轻普通节点的负担并保持持续的连通性，许多研究人员建议部署某些特殊节点作为中继节点。这些特殊节点的成本相对普通节点较高。因此，一些研究致力于部署最少数量的中继节点以最小化网络成本。其他研究人员提出了使用移动边缘计算来降低传输延迟和能量消耗。此外，在文献中，移动汇聚节点被建议用于应对拓扑失效、感知覆盖减少以及延迟问题。除了连通性和覆盖约束外，许多应用具有延迟敏感性。延迟和可靠性是延迟敏感类应用中的两个关键挑战。在Ma等人的研究中，提出了一种具有最小延迟的多跳中继传输方案。
本文中，我们的第二个目标是设计一种算法，以部署最少数量的昂贵中继节点来确保完全连通性。值得注意的是，用最少数量的传感器节点覆盖N个目标以及部署最少数量的中继节点以确保传感器节点的连通性属于非确定性多项式时间（NP难）问题。针对上述节点部署问题，采用元启发式方法有助于获得有效的解决方案。粒子群优化（PSO）是一种合适的进化算法，被广泛用于解决多种优化问题。在本研究中，我们实现了一种PSO与迭代局部搜索（ILS）相结合的方法，以寻找传感器和中继节点部署的可行解。
本文的主要贡献如下：
1. 一种改进的基于粒子群优化的方法，用于选择最少数量的位置来部署传感器和中继节点，以满足目标点的全覆盖以及已部署传感器节点的连通性。
2. 一种高效的算法，用于计算一些可选位置以部署中继节点。
3. 使用ILS方法来提升粒子群优化算法的性能。
本文其余部分结构如下：第2节介绍了相关研究工作。第3节概述了所使用的算法。第4节介绍了我们提出的协议；第5节展示了分析和实验结果。最后，第6节得出结论。
相关工作
节点部署对无线传感器网络的覆盖、数据延迟、连通性、部署成本和寿命有巨大影响。因此，在过去十年中，无线传感器网络中的节点部署受到了广泛关注。节点部署问题的主要目标是在保持感知区域完全覆盖和网络连通性的前提下，以最低的部署成本放置最少数量的节点。优化算法在处理无线传感器网络中的最优节点布置问题时具有重要作用。
在哈里赞和库伊拉的研究中，采用了一种改进的遗传算法（GA）来求解多目标覆盖问题的可行解。该算法的四个相互冲突的目标是：(1) 激活尽可能少的传感器节点，(2) 实现对所有目标点的最大覆盖，(3) 保持活跃传感器节点与汇聚节点之间的通信，以及(4) 确保选择剩余能量较高的传感器节点作为活跃节点。
在古普塔和贾的研究中，采用了一种基于生物地理的优化（BBO）方案，用于寻找放置传感器节点的最佳位置数量，以确保满足k‐覆盖和m‐连通性要求。所提出的基于BBO的方案提供了一种合适的栖息地表示编码方案，并设计了目标函数以及BBO的迁移和变异算子。一种基于遗传算法（GA）的方法被提出，用于部署传感器节点以实现最大程度的覆盖。为解决该问题，应用了基于蒙特卡洛的数学建模与仿真。考虑了两个相互冲突的目标：（1）最大化区域覆盖；（2）最小化所选传感器的数量。然而，未考虑连通性。
此外，提出了一种基于遗传算法的节点部署方法，以满足对给定目标点集的k‐覆盖和传感器节点的m‐连通性。本文所考虑的多目标节点部署问题包含三个目标：（1）激活尽可能少的传感器节点，（2）实现完全覆盖，（3）保持网络连通性。
需要注意的是，雷拜等人提出了一种新型的遗传算法，用于寻找放置最少数量传感器节点的不同位置。该算法的主要目标是在部署最少数量的传感器节点的同时，最大化已部署传感器之间的连通率，以覆盖感知区域。
在阿里武达伊南比等人中，提出了一种名为布谷鸟搜索算法的受自然启发的进化算法，用于求解目标覆盖问题中传感器的最优位置。
为了构建网络的连通性，许多研究集中在中继节点的部署上。最优中继节点放置（ORP）是无线网络中一个有趣且具有挑战性的问题。例如，有人提出了一种用于多跳无线网络中连通性优化的新型中继节点放置方法。在其方法中，分别在解决方案选择阶段和最优放置阶段设计了留一法（LOO）和粒子群优化算法。此外，还提出了一种使用多目标元启发式技术的中继节点部署方法。兰萨‐古铁雷斯和普利多采用了三个子目标：剩余能量、区域覆盖和可靠性。然而，未考虑所需连通性下的全覆盖挑战。此外，还提出了一种新颖的部署方法ACO‐贪婪，以解决基于网格的覆盖问题。该方法结合了蚁群优化与贪婪迁移机制。考虑了三个相互冲突的目标：（1）确保全覆盖，（2）降低部署成本，（3）确保连通性。类似地，在古普塔中，提出了一种基于遗传算法的中继节点部署算法。他们的工作假设节点被随机或手动部署在一个大的感知区域上，并给出了一些预选位置用于放置中继节点。目标是放置最少数量的中继节点，以实现每个节点的k‐连通性。然而，他们的方法未考虑中继节点的完全连通性。
此外，尼泰什和贾纳提出了一种中继节点定位算法。该方法保证了感知区域的k‐覆盖以及中继节点的s‐连通性。他们的算法通过最小化中继节点重叠覆盖的区域，使用最少数量的中继节点来降低网络成本。该方法基于利用贾维斯步进法技术生成的传感器节点螺旋序列。
需要注意的是，采用飞蛾火焰优化器（MFO）算法来确定中继节点部署的最优位置。主要目标是确保网络完全连通性。所提出的算法中使用了启发式全连通网络来测试网络的连通性。
在此背景下，我们的工作针对最优节点布置问题。我们方法的目标是找到放置传感器和中继节点的最少位置数量，以满足目标点的全覆盖和网络连通性。
所用算法概述
本文通过结合PSO和ILS算法提出了一种新方法，以解决节点布置问题。
二进制粒子群优化算法
PSO是一种合适的进化算法，已广泛用于求解各种优化问题。PSO过程从随机生成的可能解开始，之后根据适应度函数从种群中选择最优解。
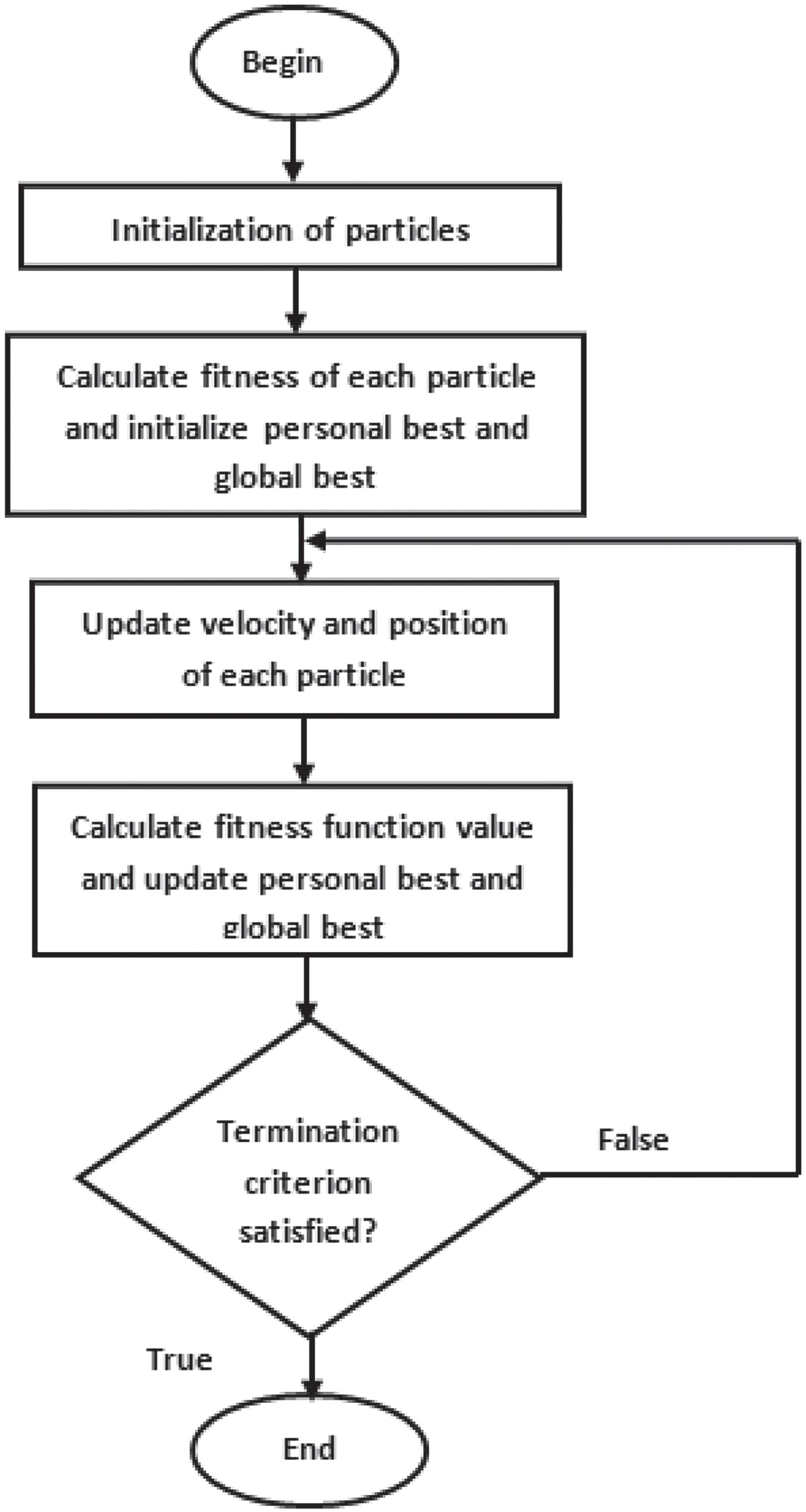
粒子群优化的各个步骤如图1所示的流程图中所示。
PSO由预定义大小（NP）的粒子群组成。粒子 $P_i, 1≤i ≤NP$ 在超空间的第 $d$ 维中具有位置 $X_{id}, 1≤d ≤D$ 和速度 $V_{id}$。
每个粒子通过适应度函数进行评估，以判断问题解的质量。在每次迭代中，其在第d维的速度$V_{id}$和位置$X_{id}$通过以下公式更新：
$$
V_{i,d}(t)= w × V_{i,d}(t−1)+ c_1 × r_1 ×(Pbest_i−X_{i,d}(t−1)) + c_2 × r_2 ×(Gbest−X_{i,d}(t−1)) \tag{1}
$$
$$
X_{i,d}(t)=X_{i,d}(t−1)+ V_{i,d}(t) \tag{2}
$$
其中，$w$ 是惯性权重，$c_1$ 和 $c_2$ 是两个称为加速因子的非负常数，$r_1$ 和 $r_2$ 是在范围 $[0,1]$ 内均匀分布的两个不同的随机数。
在我们提出的方法中，粒子的位置由二进制值表示。因此，速度必须取“0”或“1”的值。
此处使用的归一化函数是Sigmoid函数，如下所示：
$$
V’ {i,d}(t) = \text{sig}(V {i,d}(t)) = \frac{1}{1+ e^{-V_{i,d}(t)}} \tag{3}
$$
公式(1)用于更新粒子的速度向量，最后一个粒子的新位置通过以下公式获得：
$$
X_{i,d}(t+ 1)=
\begin{cases}
1 & \text{if } r_{ij} ≤ \text{sig}(V_{i,d}(t+ 1)) \
0 & \text{Otherwise}
\end{cases} \tag{4}
$$
其中$r_{ij}$是范围$[0,1]$内的均匀随机数。
迭代局部搜索
ILS是一种能够逃离局部最优的元启发式算法。它从一个局部最优解开始，在每次迭代中对该解进行扰动，以寻找全局最优。
所提出的协议
问题描述
给定M个预定义的潜在位置和一组在感知区域内随机分布的N个目标点，我们的目标是：(1) 选择最少数量的可能位置来部署传感器节点，以实现完全目标覆盖；(2) 部署尽可能少的中继节点以维持网络连通性。为了说明我们的协议，引入了以下假设：
• $P = P_1,P_2,…,P_M$ 是预定义的潜在位置集合。
• $T = {T_1,T_2,…,T_N}$ 是所有目标点的集合。
• $r_c$、$r_r$ 分别表示传感器和中继节点的通信范围（$r_r≥r_c$）。
• $r_s$ 表示传感器节点的感知范围。
• 对于位于 $(x, y)$ 的任意目标点 $T_i$，用 $d(s_i, T_i)$ 表示传感器节点 $s_i$ 与目标点 $T_i$ 之间的欧几里得距离。
$$
d(s_i , T_i) = \sqrt{(x_i −x)^2+(y_i −y)^2} \tag{5}
$$
目标$T_i$被节点$s_i$覆盖，当且仅当$d(s_i, T_i) ≤ r_s$。
覆盖目标$T_i$的传感器集合由$\text{Coverage}(T_i)= {s_j,1≤j ≤N, \setminus d(s_j, T_i)≤r_s}$定义。
如果目标$T_i$被至少k个传感器节点覆盖，则称该目标$T_i$为k覆盖，其中k是一个预定义的值： $|\text{Coverage}(T_i)| ≥ k$。
目标$T_i$的k‐覆盖定义如下方程所示：
$$
\text{cov}(T_i)=
\begin{cases}
1 & \text{if } |\text{Coverage}(T_i)| ≥ k \
0 & \text{Otherwise}
\end{cases} \tag{6}
$$
如果监测区域内的每个目标$T_i$均满足k‐覆盖，则称该区域为k‐覆盖：$∀ T_i ∈ T, |\text{Coverage}(T_i)| ≥ k$。目标区域的k‐覆盖覆盖率定义如下：
$$
P_{\text{cov}}= \frac{\sum_{i=1}^{M}\text{cov}(T_i)}{M} \tag{7}
$$
其中M为目标点数量。
$\text{Connexe}(s_i)$ 表示在 $s_i$ 的通信范围内的中继节点集合。
网络的m‐连通性是指每个传感器节点与m个其他中继节点相连。传感器节点$s_i$的m‐连通性定义如下：
$$
\text{con}(s_i)=
\begin{cases}
1 & \text{if } |\text{Connexe}(s_i)| ≥ m \
0 & \text{Otherwise}
\end{cases} \tag{8}
$$
提出的方法
在此工作中，网络由三种设备组成：基站、传感器节点和中继节点。基站具有充足的能量资源。传感器节点以确定性方式部署在有限的区域中，以确保对给定目标点的完全覆盖。传感器、中继节点和基站在部署后均保持静止。
我们的主要目标是研究传感器和中继节点的部署，以实现无线传感器网络的覆盖与连通性，并降低网络成本。
所提出方法的整体操作可总结如下：（1）使用PSO‐ILS优化普通传感器节点的部署，（2）执行最优位置确定（OPD）算法以确定候选位置，（3）执行PSO‐ILS算法以找到部署中继节点的最少位置数量，从而确保普通传感器节点的完全连通性。
降低部署成本需要减少部署的传感器节点数量。然而，某些应用具有很高的关键性，因此必须满足覆盖与连通性要求。为了保证完全覆盖和网络连通性，有必要增加传感器和中继节点的数量。显然，上述目标，即最低成本部署与最大覆盖和连通率，是相互冲突的目标。为了有效解决传感器和中继节点问题中的上述问题，采用元启发式方法是非常可取的。如算法2所示，所提出的方法称为PSO‐ILS算法，该方法基于二进制粒子群优化和迭代局部搜索算法的共同特征。开发了一种改进的局部搜索过程，以提高粒子群优化算法的性能。
最优节点部署
现在，我们讨论节点部署问题，其主要目标是以最少数量的节点保证对目标点的完全覆盖。采用PSO‐ILS算法来解决该节点部署问题。
- 初始种群的生成 。初始种群是一组以随机方式生成的粒子。粒子的维度等于网络中潜在位置的数量（M）。设$P_i =[X_{i1},X_{i2},…,X_{iM}]$为种群中的第i个粒子，其中每个分量$X_{id}$映射合适位置$s_d$的状态如下：
$$
X_{i,d}=
\begin{cases}
1 & \text{if State= selected} \
0 & \text{Otherwise}
\end{cases} \tag{9}
$$
- 适应度函数的调整 。每个粒子根据目标函数进行评估。在本研究中，我们的主要目标是选择最少数量的潜在位置，以实现对目标点的完全覆盖。我们将该问题表述为一个多目标优化问题。第一个目标是最大化网络的覆盖率
$$
f_1= \frac{\sum_{i=1}^{N}\text{cov}(T_i)}{M} \tag{10}
$$
其中N是感知区域内的目标点数量。
$\text{cov}(T_i)= 1$。数值1表示目标被覆盖，0表示未被覆盖。
第二个目标是选择尽可能少的选定位置的数量：
$$
f_2’= \frac{s}{M} \tag{11}
$$
$s$ 表示选定位置的数量，$M$ 表示潜在位置数M。为了将该目标转换为最大化问题，选定位置的数量定义如下：
$$
f_2= 1−f_2’ \tag{12}
$$
该问题由多目标适应度函数处理，其约束条件表述如下：
$$
\text{Maximize Fitness}= α_1 ×f_1+ α_2 ×f_2 \tag{13}
$$
其中 $α_1+ α_2= 1$ 和 $0≤α_i≤1；∀ i， 1≤i ≤2$
-
速度和位置更新 。在每次迭代中，分别使用公式(1)和(4)更新速度和位置。
-
改进的ILS 。我们希望从网络中移除已部署节点的冗余，而不影响覆盖。ILS方法用于提升粒子群优化算法的性能。
一个不必要的节点可以从其所属的当前解中移除，且不会降低该解的覆盖。 -
个体最优和全局最优更新 。在PSO‐ILS算法终止后（参见算法2），粒子Gbest表示用于放置传感器节点的选定位置集合。
最优中继放置
在本节中，我们介绍了ORP机制的相关细节。主要目标是用最少数量的中继节点保证网络的完全连通性。在该协议中，依次使用PSO‐ILS算法执行OPD和ORP。我们的算法假设传感器节点已在部署区域手动放置，以确保完全目标覆盖。所提出的工作可概括为以下几个阶段：
- OPD 。在这项工作中，设计了一种OPD算法，用于确定一组候选位置，这些位置随后可用于放置中继节点以进行数据转发。我们算法的目的是确保不相交段之间的节点连通性。
在OPD算法终止后，会给出一些预定义的位置，并将用于部署中继节点。下一阶段的目标是在这些预定位置上放置最少数量的中继节点，以确保每个传感器节点的k‐连通性。
- 优化的中继节点定位 。为了放置最少数量的中继节点，将使用PSO‐ILS算法（参见算法2）。粒子的维度与OPD算法（参见算法3）找到的潜在位置数M（P）相同。设$P_i=[X_{i1},X_{i2},…,X_{iP}]$为种群中的第i个粒子，其中每个分量$X_{id}$映射位置$s_d$的状态如下：
$$
X_{i,d}=
\begin{cases}
1 & \text{if State= selected} \
0 & \text{Otherwise}
\end{cases} \tag{14}
$$
每个粒子根据目标函数进行评估。主要目标是在为传感器节点提供完全连通性的同时，放置最少数量的中继节点。
该问题被表述为一个多目标优化问题。
第一个目标是最大化传感器节点的连通率：
$$
f_1= \frac{\sum_{i=1}^{N}\text{con}(s_i)}{N} \tag{15}
$$
其中，$N$ 表示区域内传感器节点的数量。
$\text{con}(s_i)= 1$。数值1表示传感器节点$s_i$已连接，否则为0。
第二个目标是最小化选定位置的数量
$$
f_2’ = \frac{n}{P} \tag{16}
$$
其中$n$为选定位置的数量，$P$表示定义的潜在位置数。为了将该目标转换为最大化问题，选定位置的数量定义如下：
$$
f_2= 1−f_2’ \tag{17}
$$
第三个目标是最大化网络中继节点的连通率
$$
f_3= \frac{\sum_{i=1}^{n} \text{connexe}(r_i)}{n} \tag{18}
$$
其中$n$是中继节点数量，与所选位置的数量相同。$\text{connexe}(r_i) = 1$。数字1表示中继节点$r_i$已连接，否则为0。该问题已被处理，被表示为一个多目标适应度函数，其约束条件可表述如下：
$$
\text{Maximize Fitness}= α_1 ×f_1+ α_2 ×f_2+ α_3 ×f_3 \tag{19}
$$
其中 $α_1+ α_2+ α_3= 1$ 和 $0≤α_i≤1；∀ i， 1≤i ≤3$。在PSO‐ILS算法终止后（参见算法2），最优解表示选定位置的集合。
时间复杂度
所提出的协议包含三个连续的操作：最优节点部署、OPD和最优中继节点布置。前两个操作均使用PSO‐ILS算法。该算法的时间复杂度为$O(N_i × N_P× M^2)$，其中$N_i$是PSO‐ILS的迭代次数，$N_P$是粒子数量，$M$是潜在位置数M。而OPD算法的时间复杂度为$O(S)$，其中$S$是传感器节点数量。
仿真与结果
为了评估所提出的混合方法的性能，我们进行了广泛的仿真。仿真参数见表1。
为了执行所提出的算法，表2给出了初始种群的设置以及PSO参数的值。
最优节点部署
我们通过将传感器节点数量从150变化到350，目标点从40变化到80来执行所提出的方法。我们设定$ r_s = 40m $。潜在位置和目标点在300 × 300范围内随机分布，其中基站位置为(300, 150)。
为了将我们的算法与一些相关研究进行比较，我们选择对算法进行修改。我们增加了一个第三目标，从而将连通性纳入考虑范围。
所提出的算法在传感器节点部署位置数量和网络连通性方面与差分进化、粒子群优化、和改进的遗传算法（GA）进行了比较。
权重因子 $ α_1 $、$ α_2 $和 $ α_3 $通过多次测试不同的权重值组合来选择。我们观察到，当$ α_1 = 0.25 $、$ α_2 = 0.5 $和 $ α_3 = 0.25 $时，所提出的算法提供了更好的结果。在表3中给出了多个测试权重值下目标函数$ f_1 $、$ f_2 $和$ f_3 $的值。
| 参数 | 值 |
|---|---|
| 网络区域 | (300 × 300), (500 × 500) |
| 基站位置 | (300, 150), (500, 500) |
| 目标数量 | 40–80 |
| 传感器数量 | 5–50 |
| $ r_s $ | 40 m |
| $ r_r $ | 70–120米 |
表1 仿真参数
| 参数 | 值 |
|---|---|
| NP | 40 |
| $ c_1 $ | 1.4 |
| $ c_2 $ | 1.4 |
| w | 1 |
| 迭代次数 | 200 |
表2 PSO参数
| $ α_1 $ | $ α_2 $ | $ α_3 $ | $ f_1 $ | $ f_2 $ | $ f_3 $ |
|---|---|---|---|---|---|
| 0.4 | 0.2 | 0.4 | 100 | 20 | 100 |
| 0.3 | 0.4 | 0.3 | 100 | 19 | 100 |
| 0.25 | 0.5 | 0.25 | 100 | 18 | 100 |
| 0.2 | 0.6 | 0.2 | 96 | 16 | 100 |
表3 各种权重值及实现目标的百分比
| 算法 | 所选位置的平均值 | STD |
|---|---|---|
| PSO | 23 | 1.51 |
| DE | 23 | 1.28 |
| 改进型遗传算法 | 21 | 1.06 |
| PSO‐ILS | 19 | 0.7 |
表4 选定位置和标准差方面的比较
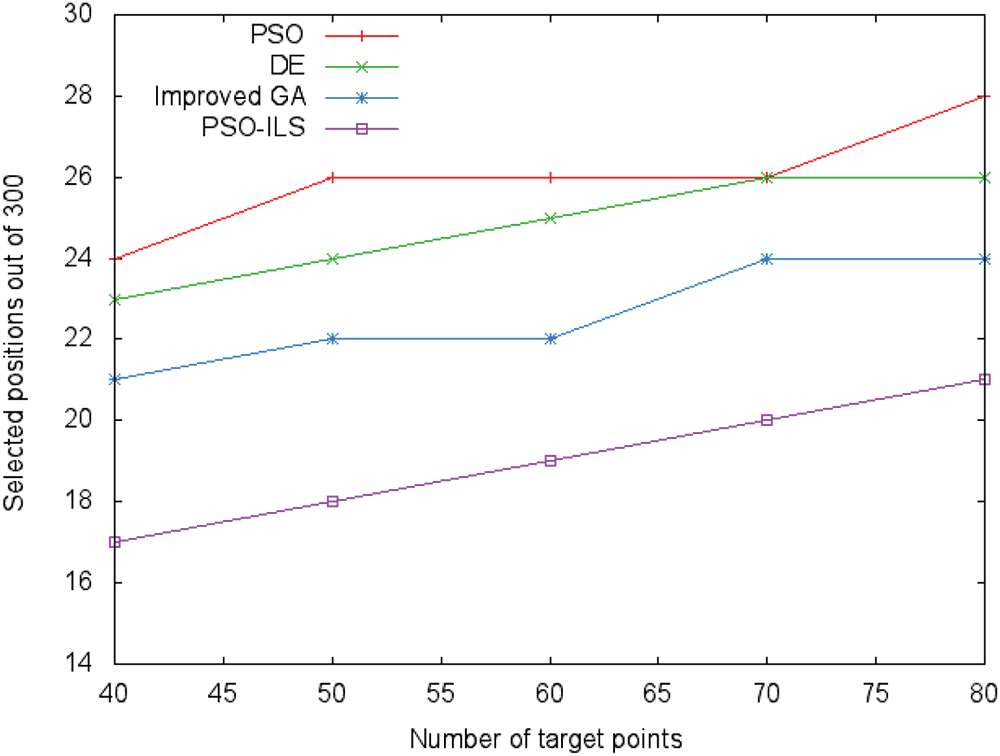
如图2所示，随着目标点数量的增加，所需的位置数量也随之增加。然而，与另外三种算法相比，所提出的算法在放置传感器节点时所需的位置数量较少。
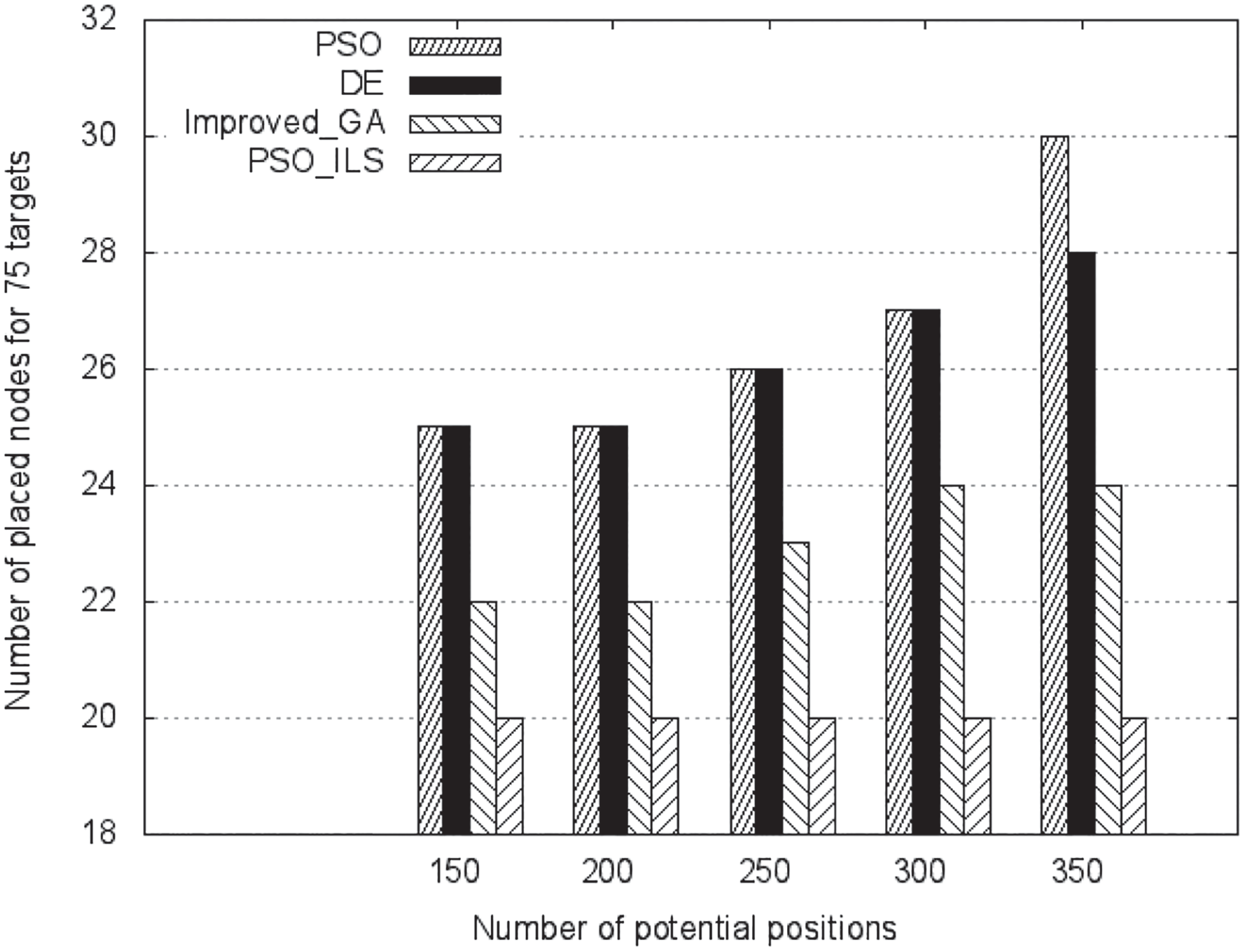
如图3所示，我们可以观察到，与其他协议相比，我们的混合算法能够成功找到最优解。该解决方案以最少数量的传感器保证了网络的完全覆盖。随着潜在位置数量的增加，我们的算法所选定位置的数量保持在大致相同的水平（约20个），而其他算法的选定位置数量则随着潜在位置数量的增加而增加。
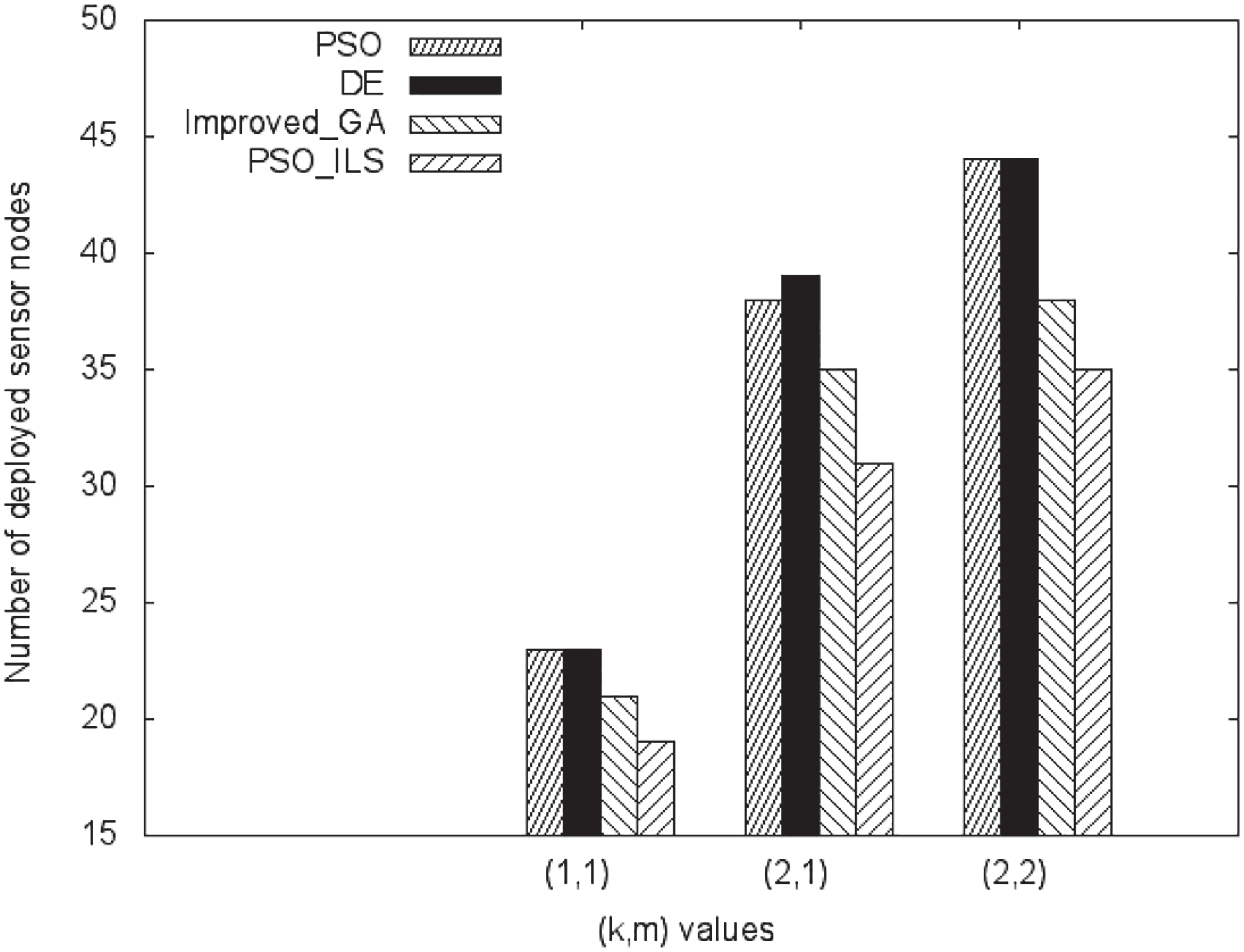
如图4所示，与其他算法相比，我们所提出的算法在确保k‐覆盖和m‐连通性的前提下，选择了最少的位置数量用于节点部署。
所提出的混合算法在寻找最少所需位置数量方面，相较于基于粒子群优化、基于差分进化和基于遗传算法的方案，在不同(k, m)组合下均表现出更优性能，以确保完全目标覆盖并维持网络连通性。
最优中继节点布置
为了评估我们算法的性能，将预定义数量的传感器节点随机放置在(300 × 300 m)区域内。传感器节点数量从20变化到50。每个节点的通信范围为80米。基站位于位置(300, 150)。
在本实验中，我们考虑了50个传感器节点，并将潜在位置的数量从150到300进行变化。我们评估了为满足网络完全连通性所需的选定位置数量。
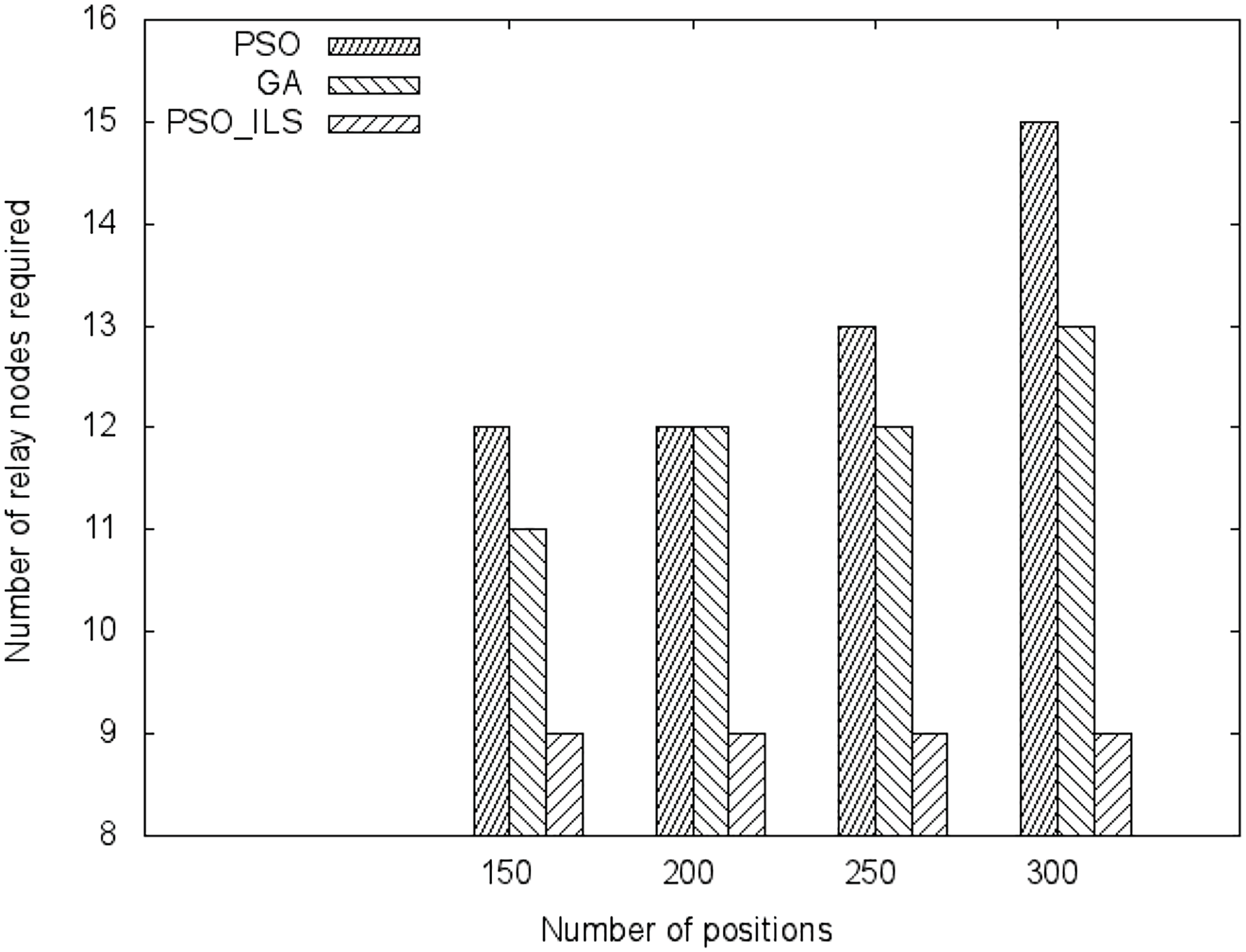
如图5所示，可以看出，与PSO和遗传算法相比，我们的改进算法具有最少的选定位置数量。随着潜在位置数量的增加，所提出的算法保持了大致相同的选定位置数量（约9个），而其他算法的选定位置数量则随潜在位置的数量增加而增加。
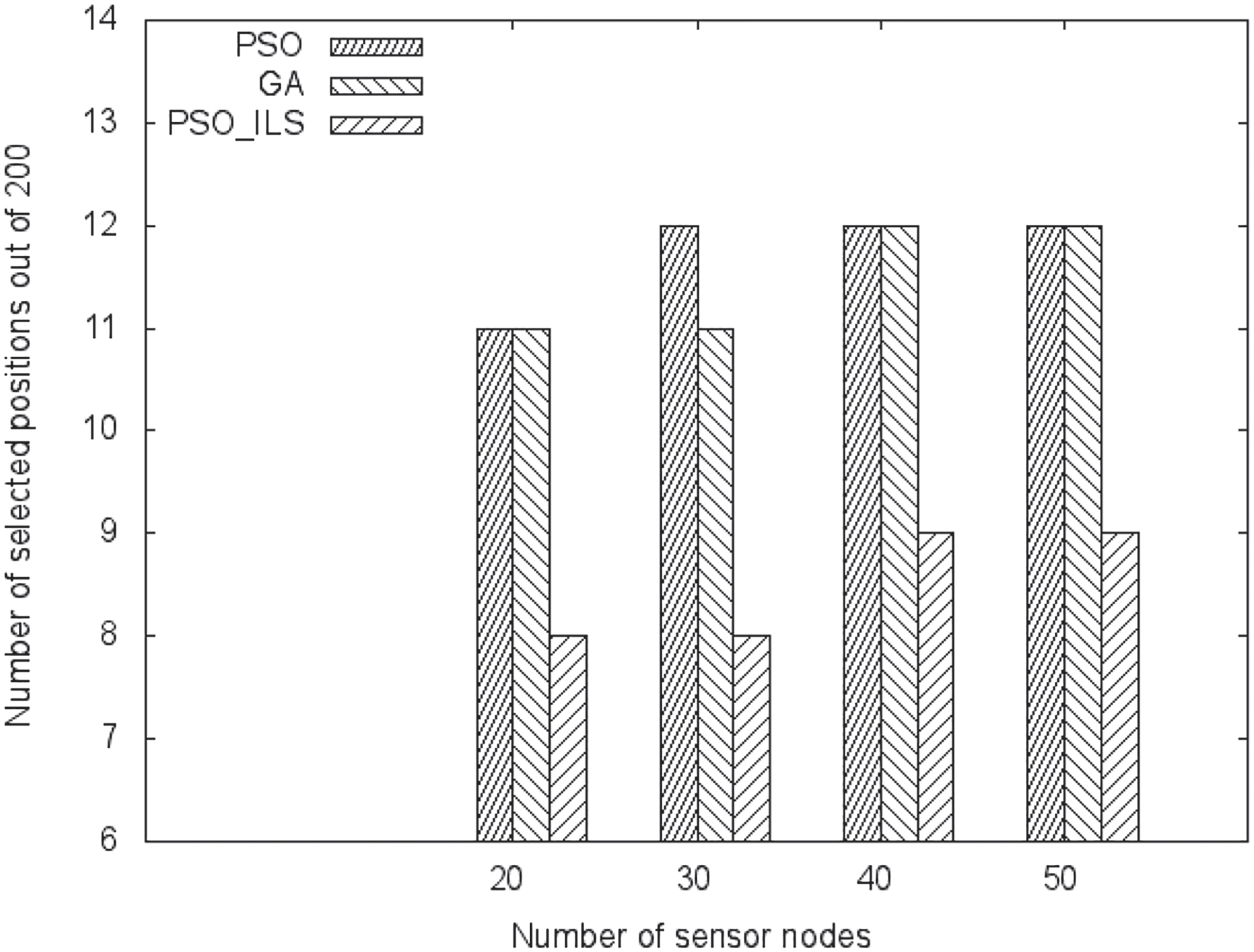
如图6所示，与其他算法相比，所提出的算法选择了确保完全连通性的中继节点部署的最少位置数量。
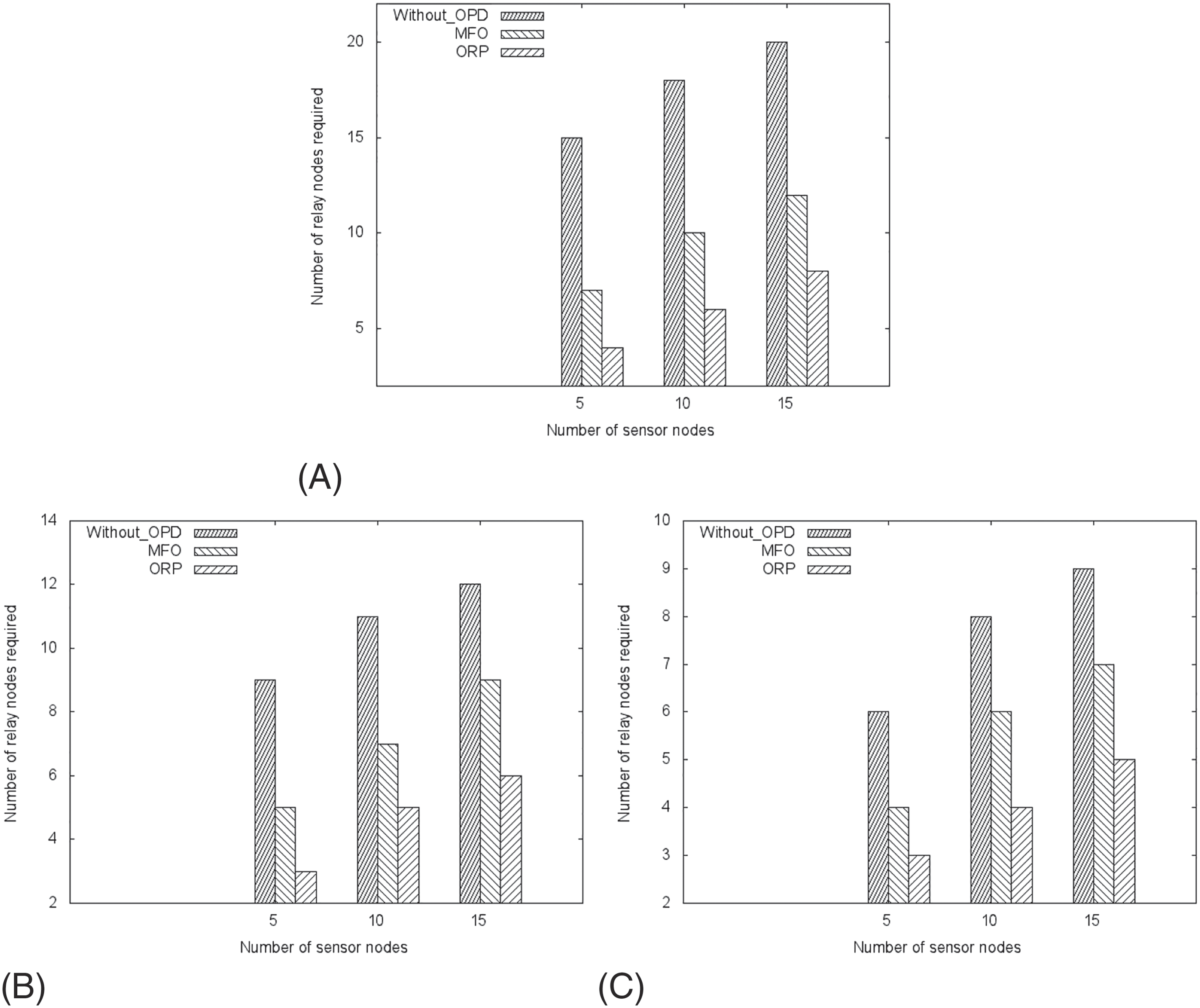当 rr = 80 时所需中继节点数量；(B) 当 rr = 100 时所需中继节点数量；(C) 当 rr = 120 时所需中继节点数量)
在以下实验中，所提出的方法ORP的性能通过满足传感器节点完全连通性所需的中继节点数量进行评估。该方法包含两个步骤：第一步使用OPD算法，第二步使用PSO‐ILS算法。第一步的目标是确定中继节点的一组潜在位置；随后，利用PSO‐ILS算法识别出最佳位置。所提出的算法与MFO以及采用随机位置的ORP在保证网络完全连通性所需的中继节点数量方面进行了比较。图7给出了当部署的传感器节点数量从5变化到15时所需中继节点数量的对比结果。这些节点部署在(500 × 500 m)的区域中，每个节点的通信范围在80到120之间变化。基站位于位置(500, 500)。
从图7可以看出，我们的OPD算法以确定性方式选择了一系列候选位置，这有助于所提出的方法在实现完全连通性时相比其他采用随机位置的算法选择最少数量的中继节点。该对比显示了OPD算法在确定中继节点候选位置方面的贡献，结果表明ORP在所需中继节点数量方面具有优越性。
结论
本文提出了一种混合方法来优化WSN中的节点部署。通过分析节点部署问题的优化，提出了一种改进的ILS。此外，基于PS和ILS的所提出工作与三种进化算法——差分进化、粒子群优化和遗传算法进行了比较。在本研究的第一部分中，为了找到在部署区域中满足目标点完全覆盖所需的最少可能位置数量，我们以覆盖率和选择节点数量作为每个猜测解性能的评判标准。实验分析通过改变可能位置的数量和目标点数量的场景来进行。实验结果表明，所提出的算法优于PSO、DE和GA。在第二部分中，目标是找到用于部署中继节点的最少预定义潜在位置数量，以满足传感器节点的完全连通性。实验分析通过在感知区域内改变传感器节点数量来进行。统计评估证明了所提出算法的优越性。在未来的工作中，我们将关注移动网络场景中的屏障覆盖问题。
扫一扫
885
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
