牛客 Minieye杯第十五届华中科技大学程序设计邀请赛网络赛 I-Tree(二分+树形dp)

最新推荐文章于 2025-02-20 22:49:29 发布

原创最新推荐文章于 2025-02-20 22:49:29 发布 · 282 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二分 #树形dp

=====DP===== 专栏收录该内容

24 篇文章

订阅专栏

本文介绍了一种结合树形动态规划（DP）与二分查找的算法，用于解决将一棵带权值的树分割成多个连通部分的问题，目标是最大化最小部分的总和。通过枚举答案并使用树形DP检查可行性，该算法能在较短时间内找到最优解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

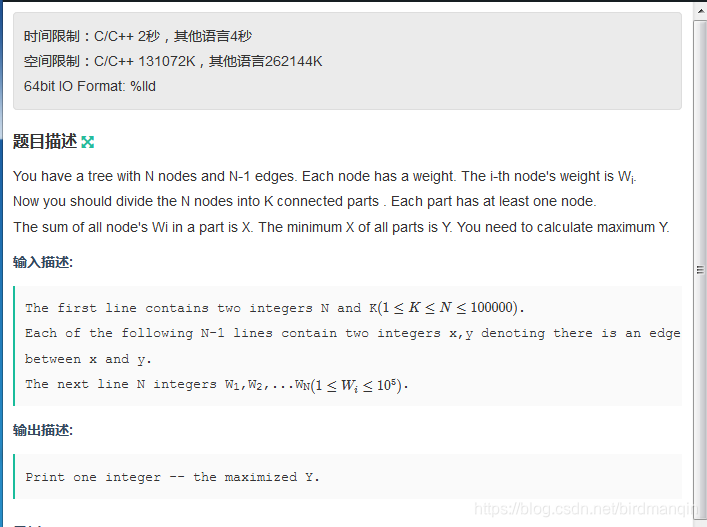
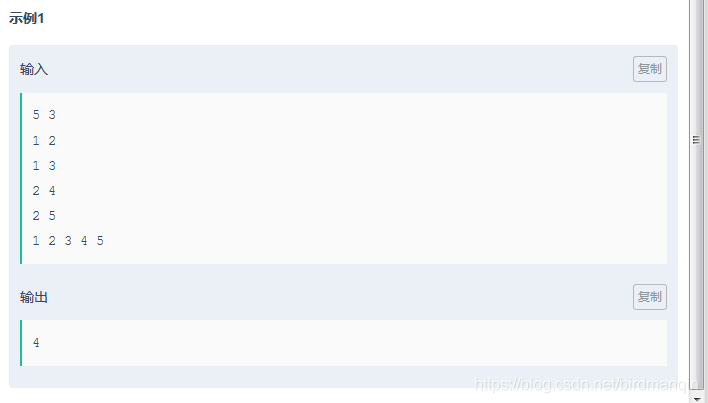
在这里插入图片描述
题意：一棵树有n个节点，每个节点有一个值，把n个节点分成k个连通的部分，使得k个部分的和的最小值最大。
思路：二分枚举答案，树形dp检查。对于一个节点v，如果他和他的子树的值小于枚举的答案
（dp[v]<x），那么他和他的子树肯定要加在他的父亲u上(dp[u]+=dp[v])；如果dp[v]>=x,则把他标记，他和他的子树形成一个连通部分。如果能形成部分大于等于k个，那肯定能由他更新到答案，所以这里的ans不用取max。
ps：坤神tql，3分钟出思路，5分钟写完ac。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#define ll long long
using namespace std;
const int N=1e5+10;
vector<int> g[N];
int n,k;
int w[N],num;
bool vis[N];
ll dp[N];
void dfs(int u,int fa,ll x)
{
	for(int i=0;i<g[u].size();i++)
	{
		int v=g[u][i];
		if(vis[v]||v==fa) continue;
		dfs(v,u,x);
		if(dp[v]<x)
			dp[u]+=dp[v];
	}
	//如果大于枚举的答案了，直接标记 
	if(dp[u]>=x)
	{
		vis[u]=1;
		num++;
	}	
}
bool judge(ll x)
{
	for(int i=1;i<=n;i++)
	{
		dp[i]=w[i];
		vis[i]=0;
	}	
	num=0;
	dfs(1,0,x);
	if(num>=k) return 1;
    else return 0;	
}
int main(void)
{
	int u,v;
	scanf("%d%d",&n,&k);
	for(int i=1;i<n;i++)
	{
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for(int i=1;i<=n;i++) 
		scanf("%d",&w[i]);
	ll l=0,r=2e10,ans=0;
	while(l<=r)
	{
		ll mid=(l+r)/2;
		if(judge(mid))
		{
			//直接更新答案 
			ans=mid;
			l=mid+1;	
		}		
		else
		{
			r=mid-1;	
		}	
	}
	printf("%lld\n",ans);
	
	return 0;	
}