What’s the Difference Between RMSE and RMSLE?

https://medium.com/analytics-vidhya/root-mean-square-log-error-rmse-vs-rmlse-935c6cc1802a

 

Introduction

There has been a lot of evaluation metrics when it comes to Regression problem and Root Mean Square Error or RMSE, in short, has been among the “goto” methods for the evaluation of regression problems and has been around since forever.

 

But recently, there has been a wildcard entry among the evaluation metrics for regression problems, especially in the Data Science competitions, and is referred to as Root Mean Squared Log Error.

At first glance, it would seem like there is just a difference of the keyword “Log” in the name of the metric. But trust me, there is a lot more to it than meets the eye. In this short article, we will be taking a closer look at RMSLE and will compare it against the RMSE metric. If you feel like you need a quick refresher on the RMSE evaluation metric, you can check out the link below

• Important Evaluation Metrics

First Look

Before taking a nosedive in the intricacies of the RMSLE, let’s take a quick look at the formulation.

 

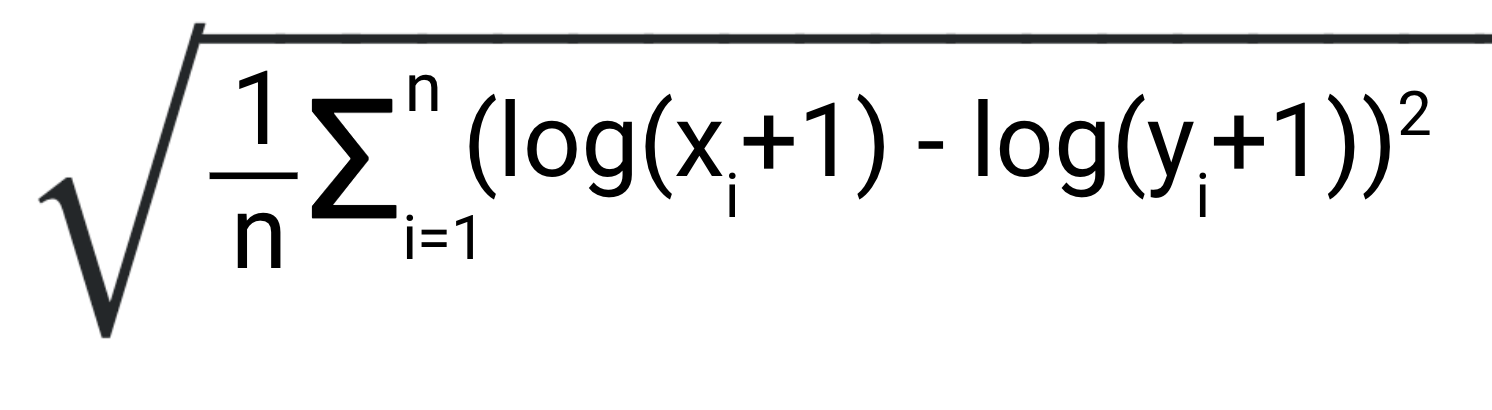
Note that in the formulation X is the predicted value and Y is the actual value.

When we see the formulation of the RMSE, it just looks like a difference of a log function. In reality, that small difference of log is the primary factor that gives RMSLE the unique properties of its own.

Let’s cover them one by one.

Robustness to the effect of the outliers

In the case of RMSE, the presence of outliers can explode the error term to a very high value. But, in the case of RMLSE the outliers are drastically scaled down therefore nullifying their effect.

Let’s understand this with a small example:

Consider the predicted value to be X and the actual value to be Y

Y = 60 80 90

X = 67 78 91

On calculating, their RMSE and RMSLE comes out to be: 4.242 and 0.6466 respectively

Now let us introduce an outlier in the data

Y = 60 80 90 750

X = 67 78 91 102

Now, in this case, the RMSE and RMSLE comes out to be: 374.724 and 1.160 respectively

We can clearly see that the value of the RMSE explodes in magnitude as soon as it encounters an outlier. In contrast, even on the introduction of the outlier, the RMSLE error is not affected much. From this small example, we can clearly infer that RMSLE is very robust when outliers come into play.

Relative Error

If we only consider the internal part of the RMLSE, we find that it is fundamentally a calculation relative error.

 

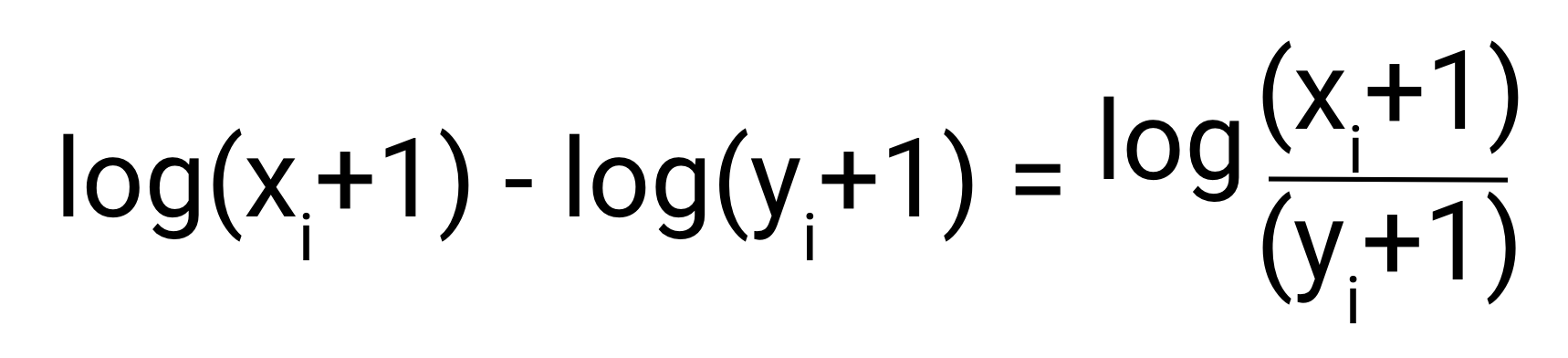
From this, we can clearly see that due to the property of Logarithms, the RMLSE can be broadly seen as relative Error error between the predicted and the actual values.

Let’s understand this with the help of an example.

Case 1:

Y = 100

X = 90

Calculated RMLSE: 0.1053

Calculated RMSE: 10

At first glance, nothing looks flashy. Let’s consider another example.

Case 2:

Consider

Y = 10000

X = 9000

Calculated RMSLE: 0.1053

Calculated RMSE : 1000

Surprised?

These two examples perfectly support the argument of the relative error which we mentioned above, RMSLE metric only considers the relative error between and the Predicted and the actual value and the scale of the error is not significant. On the other hand, RMSE value Increases in magnitude if the scale of error increases.

Biased Penalty

This is perhaps the most important factor why the RMSLE was introduced in the Data Science competitions. RMSLE incurs a larger penalty for the underestimation of the Actual variable than the Overestimation.

In simple words, more penalty is incurred when the predicted Value is less than the Actual Value. On the other hand, Less penalty is incurred when the predicted value is more than the actual value.

Let’s understand with an example.

Case 1: Underestimation of Actual Value

Y = 1000

X = 600

RMSE Calculated: 400

RMSLE Calculated: 0.510

Case2: Overestimation of Actual Value

Y = 1000

X = 1400

RMSE calculated: 400

RMSLE calculated: 0.33

From these two cases, it is evident that the RMLSE incurs a larger penalty for the underestimation of the actual value. This is especially useful for business cases where the underestimation of the target variable is not acceptable but overestimation can be tolerated.

For example:

Consider a Regression problem where we have to predict the time taken by an agent to deliver the food to customers.

Now, if the Regression model which we built overestimates the delivery time, the delivery agent then gets a relaxation on the time he takes to deliver food and this small overestimation is acceptable.

But the problem arises when the predicted delivery time is less than the actual trip takes, in this case, the delivery agent is more likely to miss the deadline, as a result, the customer reviews can be affected.

Plotting the RMSE and RMLSE

Here I am plotting the RMSE curve and RMSLE curve. For this, I simply assumed that my actual value Y is 500 and I defined a range of X from 0 to 1000. Once I defined the X and Y, I calculated RMSE and RMSLE for all the possible differences between X and Y.

These curves will clearly illustrate the point we made regarding the extra penalty for underestimation of the actual value.

 

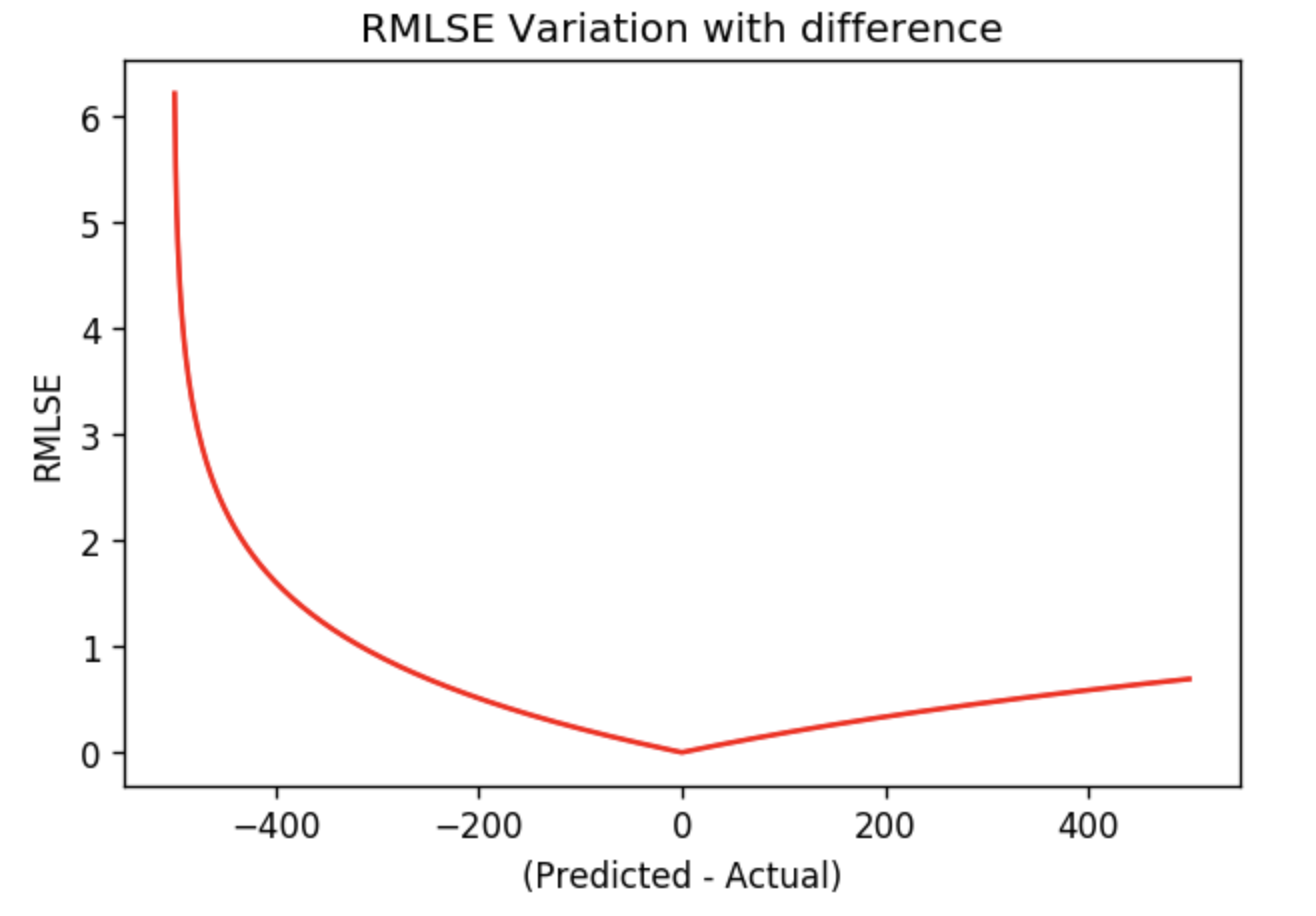
On the left half of the RMLSE curve, we clearly see that the error increases rapidly as the underestimation of actual value increases. Whereas on the right-hand side, the error is not increasing as rapidly.

 

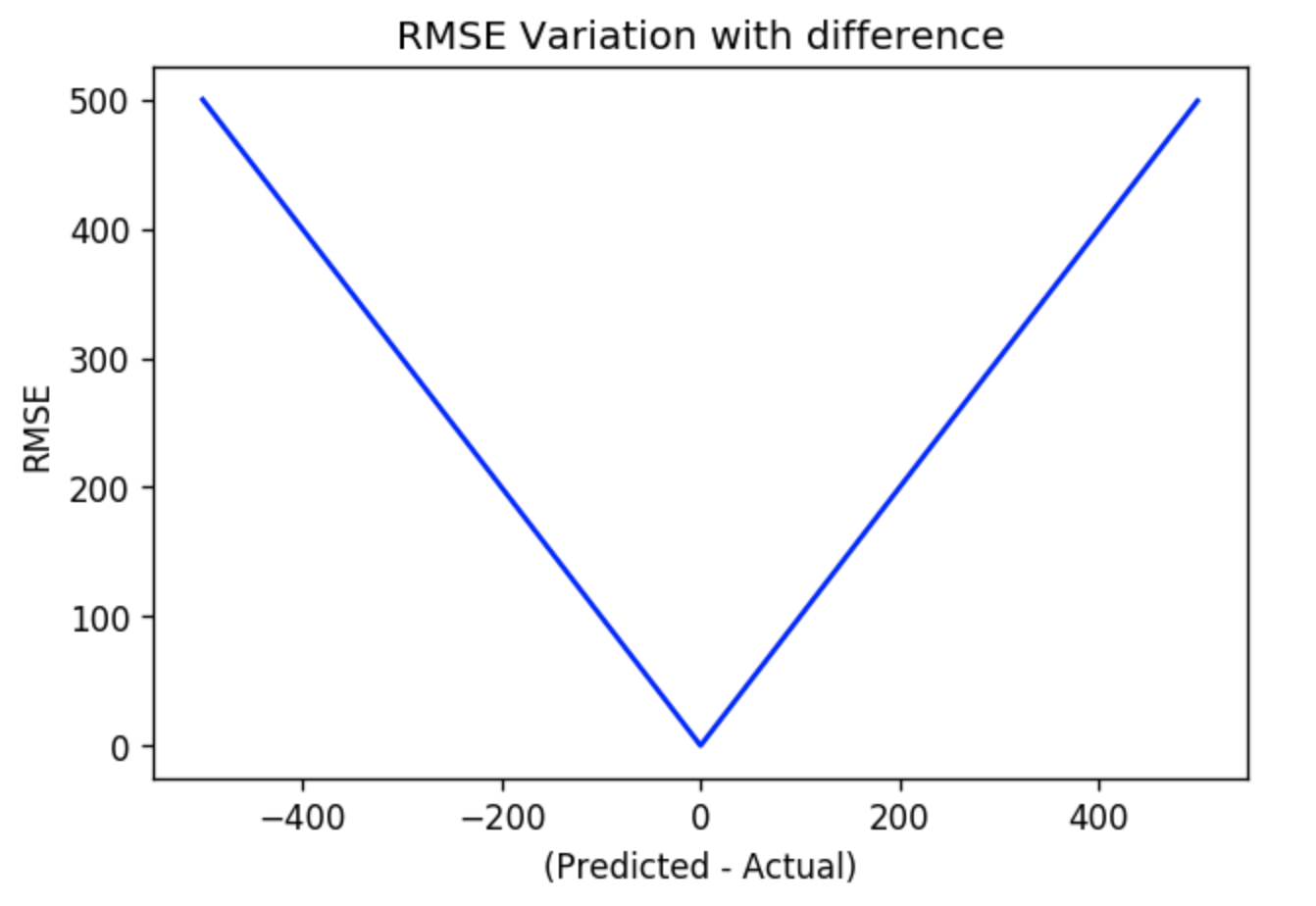
On the other hand, RMSE fails to capture any special relation between the Predicted value and the Actual Value and it is completely linear in both direction of the zero error.

 

RMSE doesn’t look that impressive anymore, does it?

Well, you should keep in mind that RMSE might still prove to be a better metric in certain scenarios. So, don’t just give up on it already.

End Notes

Here I have covered all the small details of the RMSLE metric for the regression problem. We learned about the Robustness of RMSLE to the outliers, the property of calculating the relative error between the Predicted and Actual Values, and we also learned about the most unique property of the RMLSE that it penalizes the underestimation of the actual value more severely than it does for the Overestimation.

So this brings us to the closure of this Article, I hope You are now completely aware of the RMSLE metric of Regression and all of its properties.

Analytics Vidhya

Analytics Vidhya is a community of Analytics and Data…

 

Following

 

781

 

10

 

•