可以根据这个判断是顺时针还是逆时针的
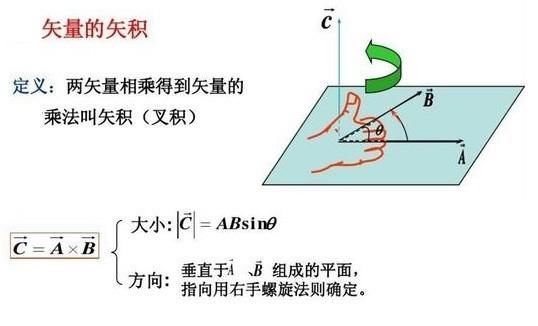
a×b的方向:四指由a开始,指向b,拇指的指向就是a×b的方向,垂直于a和b所在的平面;
b×a的方向:四指由b开始,指向a,拇指的指向就是b×a的方向,垂直于b和a所在的平面;
a×b的方向与b×a的方向是相反的,且有:a×b=-b×a。
引用自:
 本文介绍了向量叉乘的右手定则,用于判断两个向量a和b的叉乘结果方向。通过四指从a指向b,拇指的指向即为a×b的方向,且a×b与b×a方向相反。这一原理在物理学和工程计算中广泛应用。
本文介绍了向量叉乘的右手定则,用于判断两个向量a和b的叉乘结果方向。通过四指从a指向b,拇指的指向即为a×b的方向,且a×b与b×a方向相反。这一原理在物理学和工程计算中广泛应用。
可以根据这个判断是顺时针还是逆时针的

a×b的方向:四指由a开始,指向b,拇指的指向就是a×b的方向,垂直于a和b所在的平面;
b×a的方向:四指由b开始,指向a,拇指的指向就是b×a的方向,垂直于b和a所在的平面;
a×b的方向与b×a的方向是相反的,且有:a×b=-b×a。
引用自:
 6352
6352
 2825
2825