3D射线与平面交点算法，以及Unity的计算方式

安静六角

于 2025-02-25 10:16:14 发布

阅读量293

点赞数 8

CC 4.0 BY-SA版权

文章标签： 3d 平面

本文链接：https://blog.youkuaiyun.com/arkhyper/article/details/145844063

首先是通用算法：

点乘的公式是： $a\cdot b = |a|*|b|\cos \Theta$ ,示例如图所示：

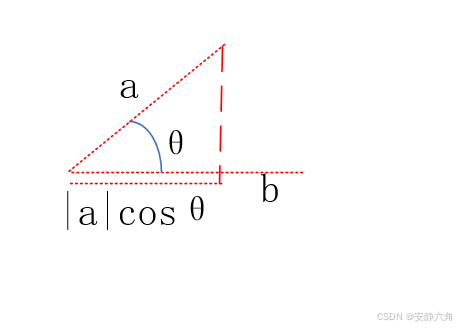
首先已知平面上的法向量，点A和平面上任意点D，求B，由于A已知求B转化为求f。

由点乘公式可知：

AD与平面法向量点乘=AB与平面法向量点乘

又：

AB与法向量点乘 = AB归一化向量*f点乘平面法向量；

ab 为AB归一化向量；

公式为： $f= \underset{AD}{\rightarrow}\cdot normal/ \underset{ab}{\rightarrow}\cdot normal$

则b点坐标为 A+f*ab

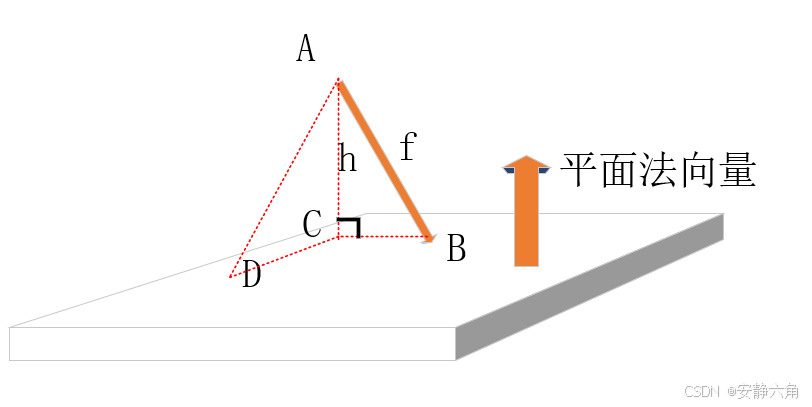
Unity 的方式为：

Ray部分代码：Origin为射线起点，Direction为归一化方向

  public struct Ray : IFormattable
  {
    private Vector3 m_Origin;
    private Vector3 m_Direction;

    public Ray(Vector3 origin, Vector3 direction)
    {
      this.m_Origin = origin;
      this.m_Direction = direction.normalized;
    }
}

平面表示代码的关键点是：Normal 表示平面归一化法线，Distance表示距离原点距离

public struct Plane : IFormattable
  {
    internal const int size = 16;
    private Vector3 m_Normal;
    private float m_Distance;
    public bool Raycast(Ray ray, out float enter)
    {
      float a = Vector3.Dot(ray.direction, this.m_Normal);
      float num = -Vector3.Dot(ray.origin, this.m_Normal) - this.m_Distance;
      if (Mathf.Approximately(a, 0.0f))
      {
        enter = 0.0f;
        return false;
      }
      enter = num / a;
      return (double) enter > 0.0;
    }
}

两者综上： $a\cdot b = |a|*|b|\cos \Theta$ ，a,b模相乘为1

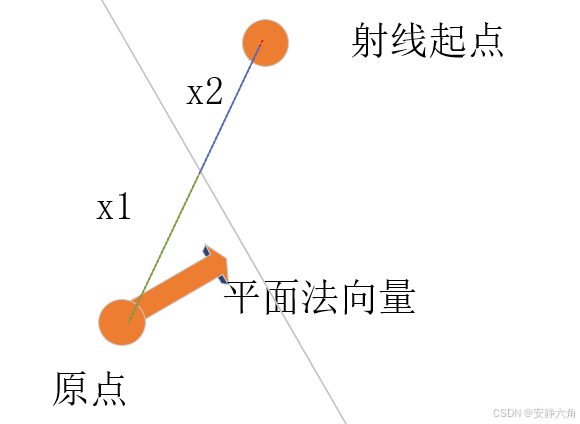
图中射线方向为原点方向

a=平面法线和射线夹脚余弦值

num = -射线的模*平面法线和射线夹脚余弦值-平面距离原点距离

则num/a = x1+x2 -x1 = x2

最终由射线起点+x2可求得交点。

RectTransformUtility中求交代码为：

public Vector3 GetPoint(float distance) => this.m_Origin + this.m_Direction * distance;

public static bool ScreenPointToWorldPointInRectangle(
      RectTransform rect,
      Vector2 screenPoint,
      Camera cam,
      out Vector3 worldPoint)
    {
      worldPoint = (Vector3) Vector2.zero;
      Ray ray = RectTransformUtility.ScreenPointToRay(cam, screenPoint);
      Plane plane = new Plane(rect.rotation * Vector3.back, rect.position);
      float enter = 0.0f;
      if ((double) Vector3.Dot(Vector3.Normalize(rect.position - ray.origin), plane.normal) != 0.0 && !plane.Raycast(ray, out enter))
        return false;
      worldPoint = ray.GetPoint(enter);
      return true;
    }