【AI深究】决策树（Decision Tree）全网最详细全流程详解与案例（附Python代码演示）|数学原理、案例流程、代码演示及结果解读|ID3、C4.5、CART算法|工程启示、分类、回归决策树

原创于 2025-06-23 17:34:44 发布 · 1.4k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#决策树 #python #算法 #人工智能 #机器学习 #ai #decision tree

【AI深究】专栏系列专栏收录该内容

36 篇文章

订阅专栏

大家好，我是爱酱。本篇将会系统讲解决策树（Decision Tree）的定义、原理、数学推导、常见算法、代码实现与工程应用。内容适合初学者和进阶读者，配合公式和可视化示例。这期的文章会较简单，如果大家有兴趣可以到爱酱主页搜寻更多分类、回归等的算法！

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、决策树是什么？

决策树是一种监督学习算法，既可用于分类（Classification）也可用于回归（Regression）。它通过一系列的“条件判断”将数据集划分成不同的子集，最终在树的叶节点给出类别或数值预测。

结构直观：类似流程图或“二十问”游戏，每个节点是一次特征判断，每个分支是判断结果，叶节点给出最终决策。
可解释性强：每一步决策都可追溯，便于业务理解和模型解释。

二、决策树的基本结构

根节点（Root Node）：包含全部数据，进行第一次特征划分。
内部节点（Internal Node）：对某个特征做条件判断（如 $X_1 < 5$ ）。
分支（Branch/Edge）：根据判断结果分流数据。
叶节点（Leaf Node）：终点，给出类别或数值预测。

例如：

判断“天气”是否晴朗，若是则继续判断“温度”，否则直接输出“不要出门”。

三、决策树的核心思想：分裂与纯度

1. 递归划分

从根节点出发，递归地选择“最佳特征”进行分裂，使得每次分裂后子集的“纯度”最大化。
纯度高意味着子集中的样本大多属于同一类别。

2. 纯度度量

常用的纯度指标有：

信息熵（Entropy）：

$p_i$ 为第 $i$ 类样本在 $S$ 中的比例。
基尼指数（Gini Index）：
方差（Variance）（回归树）：

3. 信息增益（Information Gain）

衡量分裂前后纯度提升的程度，信息增益越大，分裂越有效。

$A$ 为特征， $S_v$ 为按 $A$ 取值 $v$ 划分的子集。

四、决策树的常见算法详解

决策树算法多种多样，常见的有ID3、C4.5和CART三种，它们各有特点和适用场景。下面详细介绍这三种算法。

1. ID3算法

ID3（Iterative Dichotomiser 3）是最早的决策树分类算法之一，核心思想是用信息增益（Information Gain）选择分裂特征。

信息熵（Entropy）
衡量样本集合 $S$ 的纯度：

其中， $p_i$ 为第 $i$ 类样本在 $S$ 中的比例， $C$ 为类别数。
信息增益（Information Gain）
衡量用特征 $A$ 分裂后熵的减少量：

其中， $S_v$ 为 $A$ 取值为 $v$ 时的数据子集。
特点
- 偏向取值多的特征（可能导致过拟合）。
- 只支持离散特征，不支持连续特征和缺失值。

2. C4.5算法

C4.5是ID3的改进版，支持连续特征和缺失值，采用信息增益率（Gain Ratio）作为分裂标准。

信息增益率（Gain Ratio）
先计算信息增益，然后除以特征的固有值（Intrinsic Value）：

其中， $IV(A)$ 定义为：
特点
- 支持连续特征（通过寻找最佳切分点）。
- 能处理缺失值。
- 采用剪枝防止过拟合。
- 生成多叉树。

3. CART算法（Classification and Regression Trees）

CART是目前应用最广的决策树算法，既可做分类，也可做回归，生成二叉树结构。

基尼指数（Gini Index，分类树）
衡量集合 $S$ 的不纯度：

其中， $p_i$ 为第 $i$ 类样本的比例。
方差（Variance，回归树）
衡量集合 $S$ 的方差：

其中， $\overline{y}$ 为 $S$ 中所有 $y_i$ 的均值。
特点
- 只生成二叉树（每次分裂为两个分支）。
- 分类任务用基尼指数，回归任务用方差。
- 支持连续和离散特征。
- 可剪枝，泛化能力强。

小结对比表

算法	分裂标准	支持特征类型	树结构	主要应用	优缺点
ID3	信息增益	离散特征	多叉树	分类	简单易懂，偏向多值特征，不支持连续特征
C4.5	信息增益率	离散+连续特征	多叉树	分类	支持连续特征和缺失值，泛化能力强
CART	基尼指数（分类）/方差（回归）	离散+连续特征	二叉树	分类+回归	通用性强，支持回归，结构简单

五、决策树的优缺点与工程角色

优点

直观、可解释、无需特征缩放。
可处理数值型和分类型特征。
支持特征选择和缺失值处理。

缺点

易过拟合，需剪枝或集成方法（如随机森林）。
对样本微小扰动敏感，稳定性较差。
单棵树泛化能力有限。

工程角色

常用于业务规则建模、特征选择、基线模型。
是集成算法（随机森林、梯度提升树等）的基础单元。

六、决策树的构建流程与数学推导

1. 树的递归生长流程

选择最佳分裂特征
- 对当前节点的所有特征，计算每个特征的分裂指标（如信息增益、基尼指数减少等）。
- 选择分裂效果最好的特征和分裂点。
节点分裂
- 按最佳特征将数据划分为若干子集（CART为二叉分裂，ID3/C4.5可多叉分裂）。
- 为每个子集递归重复上述过程。
终止条件
- 当前节点样本全属于同一类别。
- 没有可用特征可分裂。
- 达到最大树深、最小样本数等预设参数。
剪枝（Pruning）
- 为防止过拟合，可采用预剪枝（提前终止生长）或后剪枝（先生成完全树再回退）策略。

2. 数学推导示例：信息增益

以ID3为例，假设当前数据集 $S$ ，对特征 $A$ 的分裂信息增益为：

$H(S)$ 为整体熵， $S_v$ 为按 $A$ 取值 $v$ 划分的子集， $|S_v|/|S|$ 为权重。
选择信息增益最大的特征进行分裂。

七、决策树的代码实现与可视化

1. 分类决策树代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.datasets import load_iris

# 加载Iris数据集
iris = load_iris()
X, y = iris.data, iris.target

# 训练决策树
clf = DecisionTreeClassifier(max_depth=3, random_state=0)
clf.fit(X, y)

# 可视化决策树结构
plt.figure(figsize=(12, 6))
plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.title('Decision Tree Visualization (Iris Dataset)')
plt.show()

代码说明：

用Iris数据集训练最大深度为3的决策树分类器。
使用plot_tree可视化树结构，每个节点显示分裂条件、样本分布和类别预测。
直观展示决策树的逐层分裂与决策路径。

2. 回归决策树代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# 生成一维回归数据
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel() + 0.2 * rng.randn(80)

# 训练回归树
reg = DecisionTreeRegressor(max_depth=3)
reg.fit(X, y)

# 预测与可视化
X_test = np.linspace(0, 5, 200)[:, np.newaxis]
y_pred = reg.predict(X_test)

plt.figure(figsize=(8, 5))
plt.scatter(X, y, color='darkorange', label='Training data')
plt.plot(X_test, y_pred, color='navy', label='Decision Tree Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Decision Tree Regression Example')
plt.legend()
plt.show()

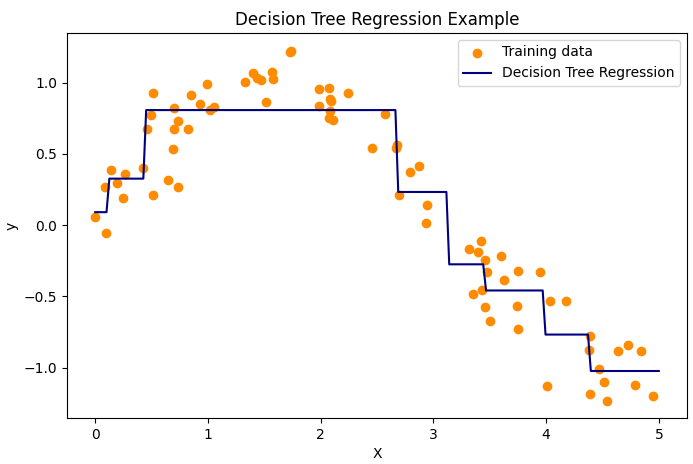
代码说明：

生成带噪声的正弦数据，训练深度为3的回归树。
可视化回归树的分段预测效果，体现其“分段常数”特性。

八、工程与教学启示

工程实践：决策树以其直观、可解释、无需特征缩放的优点，广泛应用于业务规则建模、特征选择和基线模型搭建。实际项目中，决策树常作为数据探索和可解释性分析的重要工具，也常作为集成方法（如随机森林、梯度提升树）的基础单元。工程实现时建议合理设置树的最大深度、最小样本数等参数，并结合剪枝防止过拟合。
教学应用：决策树是机器学习入门的经典算法，非常适合初学者理解模型的“决策过程”。通过可视化树结构和逐步分裂的流程，学生可以直观地看到模型如何一步步做出判断。教学中建议结合具体案例（如Iris数据集）、代码演示和树结构可视化，帮助学生建立对算法原理和应用场景的全面理解。
模型解释性：决策树的每一步判断都可追溯，便于解释模型为何做出某个预测，适合对结果可解释性要求高的场景（如金融风控、医疗诊断等）。

九、结论

决策树作为机器学习中最基础、最直观的算法之一，凭借其强大的可解释性、灵活性和对数据类型的兼容性，在分类、回归、特征选择和集成学习等领域都有广泛应用。ID3、C4.5和CART等不同算法各有优势，适用于不同的数据类型和业务需求。理解决策树的原理、优缺点和实际应用场景，不仅有助于掌握机器学习的基础知识，也为后续学习集成方法和更复杂模型打下坚实基础。

谢谢你看到这里，你们的每个赞、收藏跟转发都是我继续分享的动力。

如需进一步案例、代码实现或与其他聚类算法对比，欢迎留言交流！我是爱酱，我们下次再见，谢谢收看！