简单AI算法-决策树_ai决策树算法-优快云博客

决策树简介
通常，决策树是决策的所有可能解决方案的图形表示。如今，基于树的算法是监督学习场景中最常用的算法。它们更易于解释和可视化，具有很强的适应性。我们可以将基于树的算法用于回归和分类问题，但是，大多数时候它们都用于分类问题。
让我们通过一个例子来理解一个决策树：昨天晚上，我错过了平常的时间吃晚饭，因为我忙于处理一些事情。晚上晚些时候，我感到胃里有蝴蝶。我想如果我不饿，我就可以照原样睡觉，但事实并非如此，我决定吃点东西。我有两个选择，要么从外面点东西，要么自己做饭。
与决策树关联的术语
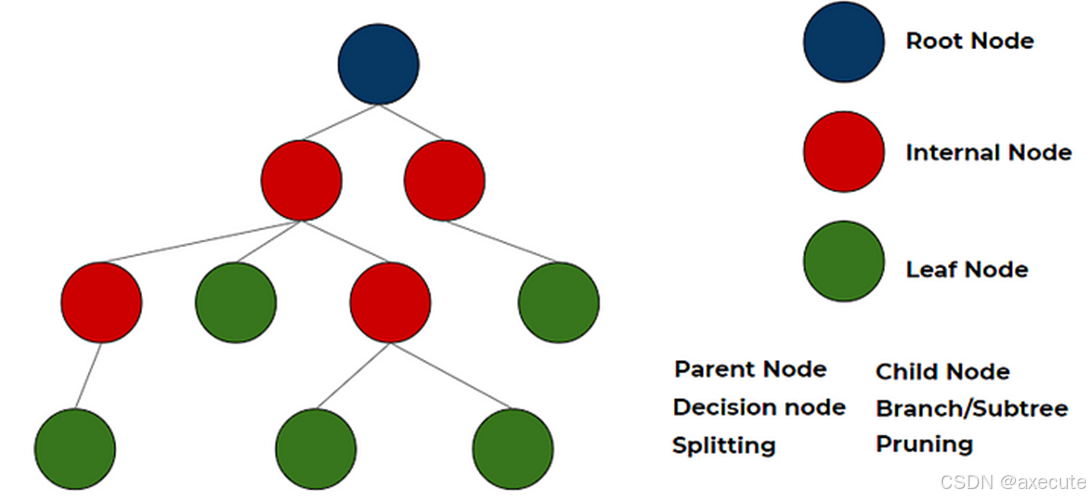
在这里插入图片描述

• 父节点：在任意两个连接的节点中，层次结构较高的节点是父节点。
• 子节点：在任意两个连接的节点中，层次结构较低的节点是子节点。
• 根节点：树开始的起始节点，它只有子节点。根节点没有父节点。（上图中的深蓝色节点）
• 叶节点/叶：树末尾的节点（没有任何子节点）是叶节点或简单地称为叶节点。（上图中的绿色节点）
• 内部节点/节点：根节点和叶节点之间的所有都是内部节点或简称为节点。内部节点同时具有父节点和至少一个子节点。（上图中的红色节点）
• Splitting：将一个节点划分为两个或多个 sun-node，或者向一个节点添加两个或多个子节点。
• 决策节点：当父节点拆分为两个或多个子节点时，该节点称为决策节点。
• 修剪：当我们删除决策节点的子节点时，它称为修剪。您可以将其理解为与拆分相反的过程。
• 分支/子树：整个树的子部分称为分支或子树。

决策树的类型
回归树
当因变量是连续的时，使用回归树。训练数据中叶节点获得的值是落在该区域中的观察值。因此，如果看不见的数据观测值落在该区域，则使用平均值进行预测。这意味着，即使训练数据中的因变量是连续的，它也只会采用测试集中的离散值。回归树遵循自上而下的贪婪方法。
分类树
当因变量为分类变量时，使用分类树。训练数据中叶子节点得到的值是观察落在该区域的模式响应，它遵循自上而下的贪婪方法。
它们一起称为 CART（分类和回归树）

从数据构建决策树

如何从表格数据创建树？应该选择哪个特征作为根节点？节点应该根据什么进行拆分？对于所有这些问题，答案都在本节中
进行战略性拆分的决定会严重影响树的准确性。每次拆分后，节点的纯度应相对于目标变量增加。决策树会拆分所有可用变量上的节点，然后选择导致最同质子节点的拆分。
以下是最常用的拆分算法

基尼杂质
Gini 说，如果我们从一个总体中随机选择两个项目，那么它们必须属于同一类，如果总体是纯粹的，则概率为 1。
它与分类目标变量 “Success” 或 “Failure” 一起使用。
它只执行二进制拆分
基尼系数越高，同质性就越高。
CART（分类与回归树）使用 Gini 方法创建二进制拆分。
计算分裂的基尼杂质的步骤
计算子节点的基尼杂质，使用公式减去成功和失败概率的平方和。
1-（p²+q²）
其中p =P（成功） & q=P（失败）
使用该分割的每个节点的加权基尼系数计算分割的基尼系数
选择分割的基尼杂质最少的特征。
卡方
它是一种算法，用于找出子节点和父节点之间差异之间的统计显著性。我们通过目标变量的观测频率和预期频率之间的标准化差的平方和来衡量它。
它与分类目标变量 “Success” 或 “Failure” 一起使用。
它可以执行两个或多个拆分。
卡方的值越高，子节点和父节点之间差异的统计显著性就越大。
每个节点的卡方使用公式
卡方 = （（实际 — 预期）² / 预期）¹/2
它会生成一个名为 CHAID（卡方自动交互检测器）的树
计算拆分卡方的步骤：
通过计算 Success 和 Failure 的偏差来计算单个节点的卡方
使用拆分的每个节点的所有成功和失败的卡方之和计算拆分的卡方
选择卡方最大位置的分割。
信息获取
不纯度较低的节点需要较少的信息来描述它，而不纯度较高的节点需要更多的信息。信息论是定义称为熵的系统中这种混乱程度的度量。如果样本是完全齐质的，则熵为零，如果样本被平均分配（50% — 50%），则它的熵为 1。熵的计算方式如下。

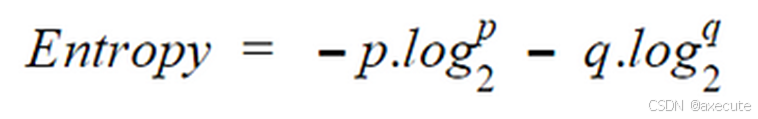
计算拆分熵的步骤：

计算父节点的熵
计算 split 的每个单独节点的熵，并计算 split 中可用的所有子节点的加权平均值。熵越小，它就越好。
按如下方式计算信息增益，并选择信息增益最高的节点进行分裂
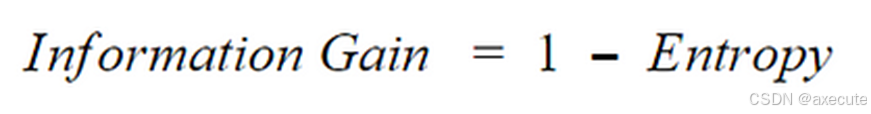
减少方差
到目前为止，我们已经讨论了分类目标变量的算法。Reduction in variance 是一种用于连续目标变量（回归问题）的算法。
用于连续变量
此算法使用标准方差公式来选择最佳分割。
选择方差较低的分割作为分割总体的标准
计算方差的步骤：
计算每个节点的方差。
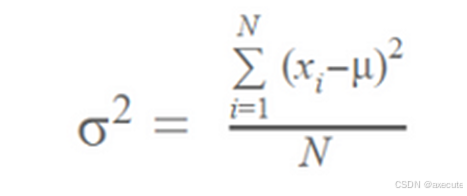
将每个分割的方差计算为每个节点方差的加权平均值。
选择方差较小的节点作为要拆分的条件。

在实践中，大多数时候使用基尼杂质，因为它为分裂提供了很好的结果并且其计算成本低廉。

避免决策树中的过度拟合
Overfit 是基于树的算法中的关键挑战之一。如果未设置限制，它将提供 100% 拟合，因为在最坏的情况下，它最终将为每个观察创建一个叶节点。因此，我们需要采取一些预防措施来避免过度拟合。它主要通过两种方式完成：

设置树大小的约束
树木修剪
让我们简要地讨论一下这两个。
设置树大小的约束
参数在树建模中起着重要作用。通过使用用于定义树的各种参数，可以避免过拟合。
节点分割的最小样本数
定义节点中考虑进行拆分所需的最小观测值数。（这确保了上述最坏情况）。
此参数的较高值可防止模型学习可能与为树选择的特定样本高度相关的关系。
过高的值会导致欠拟合，因此，应使用交叉验证对其进行适当调整。
叶节点的最小样本数
定义叶中所需的最小观察值。（同样，这也可以防止最坏的情况）
通常，对于不平衡类问题，应选择较低的值，因为少数类占多数的区域将较小。
树的最大深度（垂直深度）
用于控制过拟合，因为较高的深度将允许模型学习特定于特定样本的关系。
应使用 Cross-validation 进行适当调整，因为高度太小会导致拟合不足。
最大叶节点数
树中叶节点或叶的最大数量。
可以代替 max_depth 进行定义。由于创建了二叉树，因此深度将产生最大的叶子。n2^n
拆分需要考虑的最大特征数
搜索最佳分割时要考虑的要素数量。这些将是随机选择的。
根据经验法则，特征总数的平方根效果很好，但我们最多应检查特征总数的 30-40%。
较高的值可能会导致过度拟合，但取决于具体情况。

修剪
回想一下术语，修剪与分裂相反。现在我们看看具体情况是怎样的。让我们看看以下示例，其中绘制了药物有效性与药物剂量的关系图。所有红点都是训练数据集。我们可以看到，对于非常小和非常大的剂量，药物的有效性几乎可以忽略不计。在 10-20 毫克之间，几乎是 100%，并在 20 到 30 毫克之间逐渐减少。
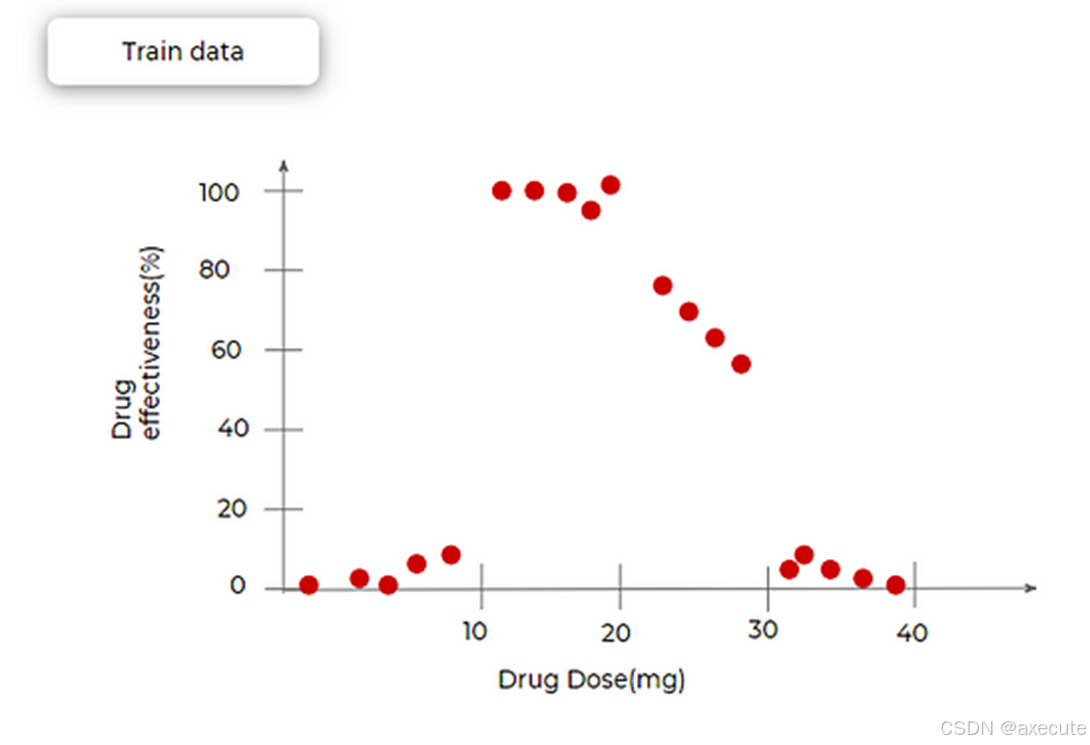
在这里插入图片描述

我们对一棵树进行了建模，并得到了以下结果。我们在三个地方进行了分裂，得到了 4 个叶节点，随着我们增加剂量，输出分别为 0（y）：0–10（X）、100：10–20、70：20–30、0：30–40。为了克服树的过拟合问题，我们决定在中间合并两个段，这意味着从树中删除两个节点，如下图所示（带有红叉的节点被删除）。现在，我们再次将这棵树拟合到训练数据集上。现在，树不太适合训练数据。但是，当我们引入测试数据时，它的表现比以前更好。这基本上就是修剪。使用修剪，我们可以避免过度拟合训练数据集。
决策树的优缺点
决策树的优点
• 易于可视化和解释：它的图形表示非常直观易懂，不需要任何统计学知识即可解释。
• 在数据探索中很有用：我们可以通过决策树轻松识别最重要的变量以及变量之间的关系。它可以帮助我们创建新变量或将一些功能放在一个存储桶中。
• 需要更少的数据清理：它对异常值和缺失数据相当免疫，因此需要的数据清理更少。
• 数据类型不是约束：它可以处理分类数据和数值数据。
决策树的缺点
• 过拟合：单个决策树往往会过度拟合数据，这可以通过对模型参数设置约束来解决，即树的高度和修剪（我们将在本文后面详细讨论）
• 不完全适合连续数据：当它将数值变量分类为不同的类别时，它会丢失一些与数值变量相关的信息。
使用 Python 实现决策树
在本节中，我们将了解如何使用 python 实现决策树。我们将使用著名的 IRIS 数据集来实现相同的目的。目的是，如果我们向这个分类器提供任何新数据，它应该能够相应地预测正确的类。
您可以在此处获取此实现的完整代码

导入所需的元器件库并读取数据
首先是导入所有必要的库和类，然后从 seaborn 库加载数据。
Python 代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.preprocessing import LabelEncoder#for train test splitting
from sklearn.model_selection import train_test_split#for decision tree object
from sklearn.tree import DecisionTreeClassifier#for checking testing results
from sklearn.metrics import classification_report, confusion_matrix#for visualizing tree 
from sklearn.tree import plot_tree

df = sns.load_dataset('iris')
print(df.head())

您应该能够获得上述数据。这里我们有 4 个特征列 sepal_length、 sepal_width、 petal_length 和 petal_width，分别具有一个目标列种类。
EDA
现在对它执行一些基本操作。

#getting information of dataset
df.info()

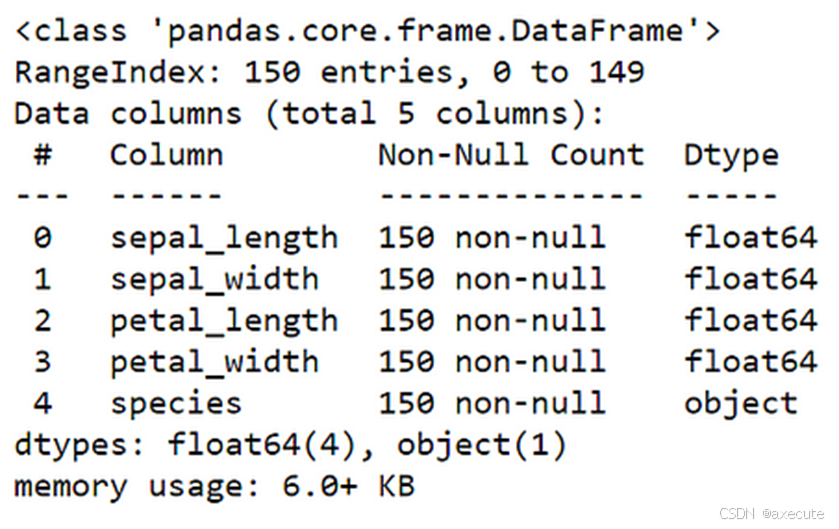
在这里插入图片描述

df.shape

我们知道这个数据集有 150 条记录，5 列，前四列是 float 类型，最后一列是对象 str 类型，并且没有 NAN 值，如下所示

df.isnull().any()

在这里插入图片描述

现在我们在这个数据集上执行一些基本的 EDA。让我们检查一下所有特征之间的相关性

# let's plot pair plot to visualise the attributes all at once
sns.pairplot(data=df, hue = 'species')

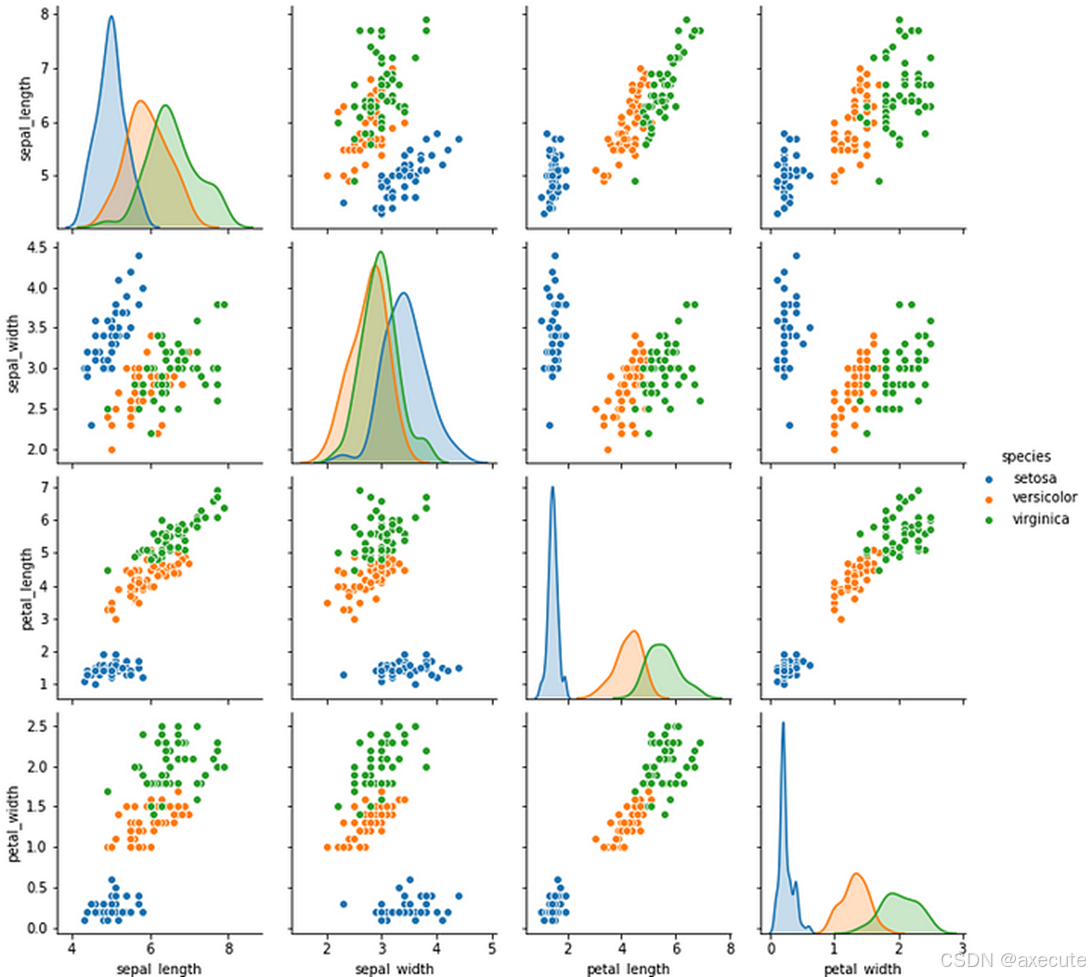
在这里插入图片描述

我们总共有 3 个物种需要预测：setosa、versicolor 和 virginica。我们可以看到，濑户总是形成与其他两个不同的集群。

# correlation matrix
sns.heatmap(df.corr())

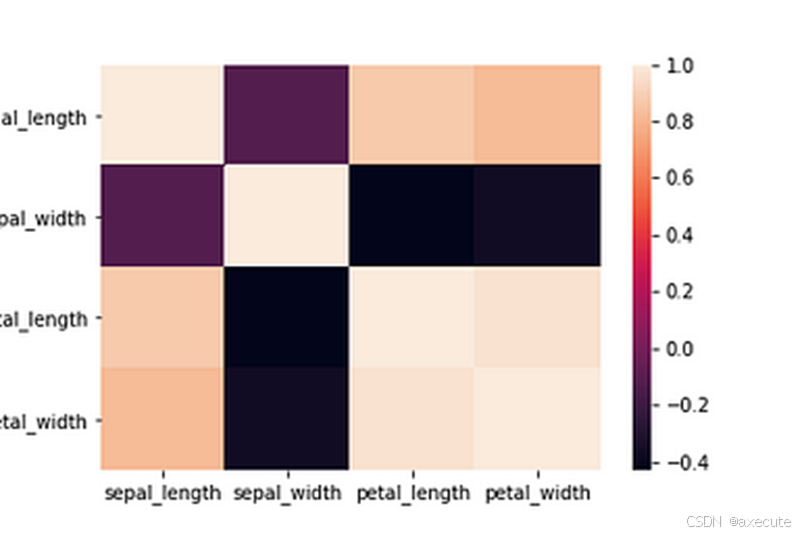
在这里插入图片描述

我们可以从以上两个图中观察到：

濑户总会形成一个不同的集群。
花瓣长度与花瓣宽度高度相关。
萼片长度与萼片宽度无关。
数据预处理
现在，我们将目标变量（y）和特征（X）分开，如下所示

target = df['species']
df1 = df.copy()
df1 = df1.drop('species', axis =1)

最好不要在原始数据集中删除或添加新列。复制它，然后对其进行修改，这样如果事情没有按照我们的预期进行，我们就可以用不同的方法重新开始原始数据。
为了遵循最常用的约定，我们将dfX

# Defining the attributes
X = df1

现在让我们看看我们的 target 变量

target

在这里插入图片描述

target中存储了分类变量，我们会将其编码为数值以供工作。

#label encoding
le = LabelEncoder()
target = le.fit_transform(target)
target

在这里插入图片描述

我们得到它的编码如上，setosa：0， versicolor：1， virginica：2
同样，为了遵循标准命名约定，将targety

y = target

将数据集拆分为训练集和测试集。随机选择 20% 的记录进行测试

# Splitting the data - 80:20 ratio
X_train, X_test, y_train, y_test = train_test_split(X , y, test_size = 0.2, random_state = 42)print("Training split input- ", X_train.shape)
print("Testing split input- ", X_test.shape)

在这里插入图片描述

拆分数据集后，我们有 120 条记录（行）用于训练，30 条记录用于测试目的。
建模树并对其进行测试

# Defining the decision tree algorithmdtree=DecisionTreeClassifier()
dtree.fit(X_train,y_train)print('Decision Tree Classifier Created')

在上面的代码中，我们创建了一个类的对象，将其地址存储在变量中，因此我们可以使用 .然后我们将这棵树与我们的和 .最后，我们在构建决策树后打印该语句。

DecisionTreeClassifierdtreedtreeX_trainy_trainDecision Tree Classifier Created
# Predicting the values of test data
y_pred = dtree.predict(X_test)
print("Classification report - \n", classification_report(y_test,y_pred))

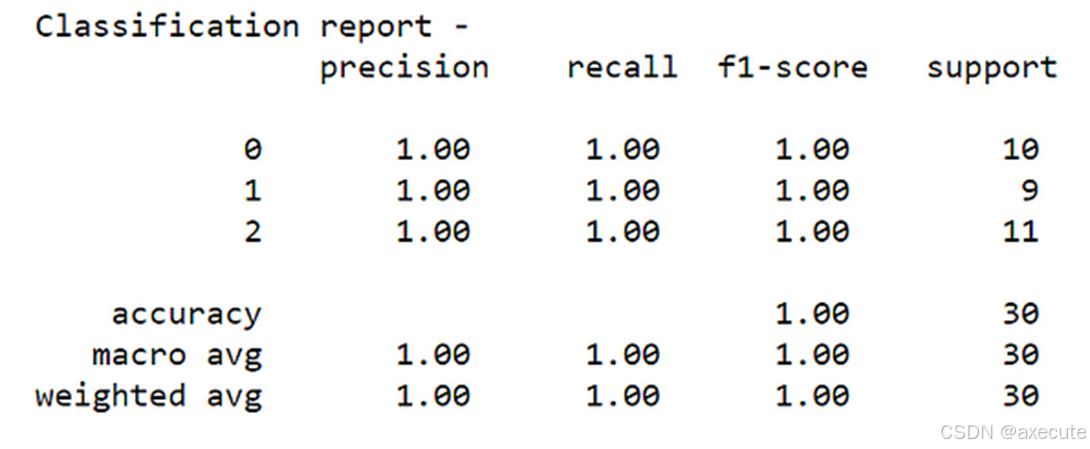
在这里插入图片描述

我们在 30 条记录的测试数据集上获得了 100% 的准确率。
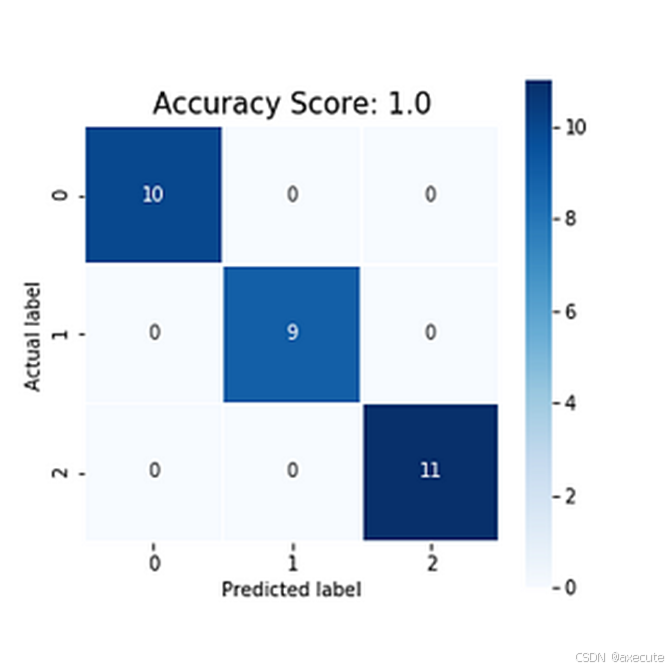
让我们绘制混淆矩阵，如下所示

cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(5,5))sns.heatmap(data=cm,linewidths=.5, annot=True,square = True,  cmap = 'Blues')plt.ylabel('Actual label')
plt.xlabel('Predicted label')all_sample_title = 'Accuracy Score: {0}'.format(dtree.score(X_test, y_test))
plt.title(all_sample_title, size = 15)

在这里插入图片描述

可视化决策树
我们可以使用以下命令直接绘制我们构建的树

# Visualising the graph without the use of graphvizplt.figure(figsize = (20,20))
dec_tree = plot_tree(decision_tree=dtree, feature_names = df1.columns, 
                     class_names =["setosa", "vercicolor", "verginica"] , filled = True , precision = 4, rounded = True)