【自校正控制】批处理最小二乘法

前言

自校正控制是自适应控制中的一种，想要学习自校正控制的话，需要先学习系统辨识，系统辨识中比较常见的是最小二乘法，因此后续会先介绍最小二乘法，再去完成自校正控制。

最小二乘法原理

假定我们有一个系统传递函数为 G = b0 / (a0 * s^2 + a1 * s + a2)，那么我们可以将其转换为状态方程的形式，方便后期处理：

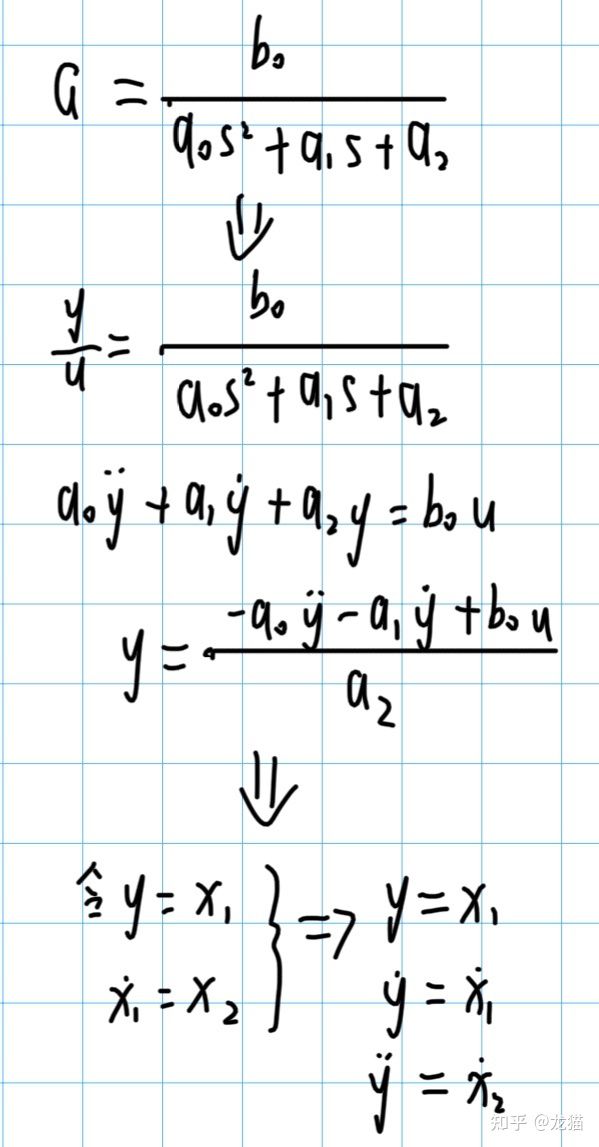
之后可以将上面的微分方程写出如下的形式：

根据上面的微分方程，我们可以将各个数据分解为两个部分，一部分为数据向量，记作φ；另一部分为参数向量，记作θ。根据上式就可以将输出 y 用这两个向量来表示，即：

y = φ' * θ ：

上面将估计输出 y_hat 也一起写出了，θ_hat 便为估计参数。我们的目的就是把估计参数 θ_hat 计算出来。

批处理最小二乘法

批处理最小二乘法是使用在采集完所有数据之后，我们采集完后，可以将数据集写出来：

引入一个估计误差的变量，记作 e：

之后可以根据误差 e，写出最小二乘的指标函数 J：

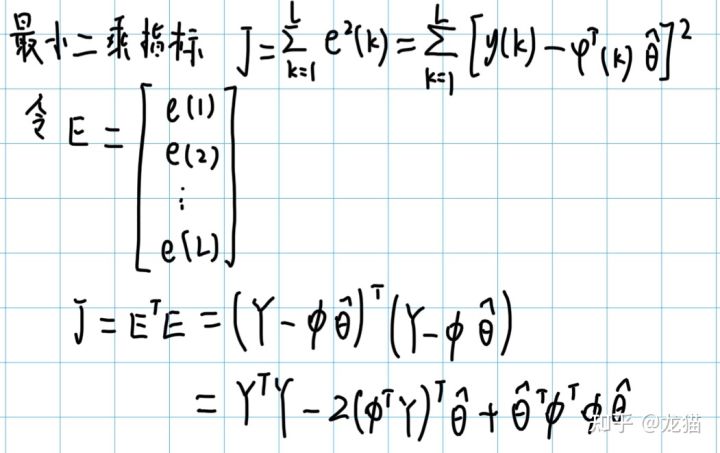
对 J 求导，便可以得到估计参数 θ_hat 的极值，进而写出估计参数 θ_hat 的表达式：

至此，便得到使用批处理最小二乘法进行系统参数估计的表达式。采集完数据之后，便可以得到估计参数矩阵 θ_hat ，进而可以转化为传递函数参数。

当然批处理最小二乘法是一种数据预处理的方法，它适合进行系统参数的初步预估，并不适合实时估计，用于数据的预处理是可以的。当然，毕竟其是一种时域数据的处理方法，对高频的数据，其处理的结果还是会有所偏差。