小学生计算思维影响因素探究

探究影响小学生协作机器人中计算思维技能的因素

威廉·H·斯图尔特1 ,杨京允2,吉娜·奎德3,和凯莉·泰勒4

摘要

近年来，教育机器人已扩展到传统STEM领域之外的课程中，并可用于培养计算思维（CT）技能。先前的研究表明，与计算思维相关的跨学科益处众多，但这些影响因素通常仅通过较少的变量进行研究。本研究通过假设一个模型，探讨了可能导致四年级和五年级小学生在协作机器人活动中发展计算思维技能的因素，该模型提出问题解决量表、内在动机和愉悦感是计算思维技能的主要预测因子。随后通过对学生进行多项心理测量量表的调查来检验该模型，并在此基础上构建了一个修订模型。研究发现感知能力与愉悦感、学习动机以及内在动机之间存在显著关系。另一个重要发现是，问题解决是计算思维技能的显著预测因子。结果结合了在教育环境中使用协作机器人改进学习成果的可能途径的相关启示进行了解释。

1韩国外国语大学，首尔，大韩民国
2博伊西州立大学教育技术系，爱达荷州博伊西，美国
3西阿达学区伽利略STEM学院，爱达荷州伊格尔，美国
4博伊西学区，爱达荷州博伊西，美国
通讯作者：杨京允，博伊西州立大学，西大学路1910号，博伊西，ID83725，美国
邮箱：youngkyunbaek@boisestate.edu

教育计算研究杂志0(0)1–32!The Author(s)2021文章重复使用指南: s a gepub.com/journals‐permissions DOI:10.1177/0735633121992479 journals.sagepub.com/home/jec

本文档由funstory.ai的开源PDF翻译库BabelDOCv0.5.10(http://yadt.io)翻译，本仓库正在积极的建设当中，欢迎star和关注。

在教育环境中使用协作机器人时改进学习成果的可能途径。

关键词

机器人技术，协作式机器人技术，计算思维技能，学习偏好，感知能力，愉悦感，内在动机，问题解决量表，小学

引言

教育机器人的使用有可能显著影响各级科学与技术教育的性质（Alimisis, 2013；Altin&Pedaste,2013），因此，学校目前正在通过各种教育机器人平台（例如乐高头脑风暴）扩大教育机器人的应用。然而，机器人技术在很大程度上仍是科学、技术、工程和数学（STEM）教育的一个组成部分（ Chalmers,2018；Goh&Ali,2014；Sullivana&Heffernana,2016； Tuluri,2015）。例如，机器人技术课程可以聚焦于基础的编程活动（Jung &Won,2018；Tocha´ cekaetal.,2016），以控制机器人的物理操作。儿童和年轻学生可能会觉得这很有趣且具有吸引力，因为他们能够直接与机器的电气和机械过程及组件进行互动。

近年来，教育机器人已被引入到STEM学科以外的其他课程领域，如艺术（Burhans&Dantu，2017；Chung，2014；Yanco等，2007）和音乐（Chung等，2014），甚至被应用于跨学科课堂（Birk，2011；Heuer等， 2017；Sabanovic等，2007）。尽管学生普遍对引入机器人持积极态度，但在不同课程中融入机器人技术的学习目标各不相同。例如，Y.Chen和 Chang（2018）报告称，当机器人技术与STEM结合时，学生对机器人的看法显著更加积极，因为它增强了学生在机器人相关领域的知识、兴趣和职业倾向。Eteokleous‐Grigoriou和Psomas（2013）发现，当机器人作为跨学科学习工具引入时，学生认为他们的课程更有趣且更具吸引力。将机器人技术融入课程的其他原因还包括创建真实的学习环境（Khanlari，2016）以及培养21世纪技能（Alimisis，2013；Khanlari，2016；Jung&Won，2018），例如提升学生的创造力、协作与团队合作、自主性、沟通能力、社交与跨文化技能以及社会责任感。

机器人活动也从简单组装（Cook等，2010；Poletz等，2010）到编程（Baek 等，2019；泰勒和白，2018，2019）不等。

2 教育计算研究杂志0(0)

编程机器人可以从使用拖放用户界面到更复杂的基于文本的编程语言。编程可以是从通过机器人底盘上的数字键盘进行基本指令输入，到使用带有互连模块的复杂图形用户界面作为可视化编程隐喻。更高级的学生可以学习用复杂的基于文本的语言编写技术代码。然而，学校中编程的主要目的往往集中在问题解决技能上，以帮助学生为未来的大学和职业发展做好准备。相比之下，将编程与机器人技术相结合，能使学生以更具体的形式展现他们的思维。当学生编程时，他们练习元认知，并能识别自己的思维错误。这些错误随后会表现为机器人中的故障（例如，向左移动而不是向右）。这种实践更通俗地称为调试。现有研究（例如，Eguchi，2012；Grandgenett等，2012；Hwang和Wu， 2014）已确定了学生在编程机器人时可在多个内容领域（包括社交互动）实现的众多教育目标。其中一个发展目标是计算思维（CT）。

机器人技术与计算思维

与机器人技术相关的计算思维是一个新兴的研究领域。由于机器人技术被视为整合和实践计算思维的跨学科路径（Shoop等，2016），自2006年计算思维技能成为热点话题以来（参见Wing，2006），相关研究兴趣不断增长。例如， G.Chen等（2017）设计了一项机器人课程，要求参与者遵循三个步骤：在纸上编写代码、在虚拟机器人上测试代码，然后将经过测试的代码在实体机器人上运行。他们发现，这些活动和课程提升了学生的计算思维，尤其是在机器人编程背景下。在另一项研究中，Barate等（2017）为小学生组织了使用乐高积木的音乐记谱活动，其中每块积木代表一个音符。学生通过以不同形状、颜色和位置配置或重新配置积木，创作出独特的乐谱。该课程不仅成为提升音乐技能的合适学习框架，同时也传递了计算思维概念。在另一项研究中， Sullivan和Bers（2016）表明，早在学前班前阶段，儿童就能掌握基础机器人编程概念，而年仅七岁的儿童便能够掌握诸如条件语句等复杂的编程概念。

Lieto等（2017）也发现教育机器人对机器人编程技能具有显著影响，并报告了机器人技术对五到六岁儿童产生的短期有益效果。正如这些研究所示，教育者可以在小学阶段的课程中尽早融入计算思维技能与机器人技术。

在计算思维技能和机器人技术方面，Taylor和Baek（2018）得出结论：小组角色影响了学生计算思维

斯图尔特等人 3

计算思维技能。白等人（2019）还发现，参与者在对机器人进行编程时，其计算思维技能显著提升。然而，以小组形式开展机器人技术活动可能对学生带来积极和消极两方面的影响。在课堂上或课后进行机器人项目时，学生通常以小组或同伴合作的形式工作。由于机器人套件数量有限（Eguchi，2012；米尔斯等人，2013；袁等人，2014），加之小组合作能为学生带来学习、动机和社会技能等方面的潜在益处，因此在机器人教学中推荐采用小组合作方式。

然而，群体动力学有时会导致部分学生参与机会减少，从而降低学习动机，或导致体验不佳。当机器人活动为协作性质时，分组方式以及学生对小组工作的既有感受可能会产生相应影响（黄和黄，2011；泰勒和白，2019）。

当从促进计算思维技能的角度来看待机器人技术活动时，导致学生成功的因素可以与许多心理特征和态度相结合，其中一个因素是学生偏好的学习互动方式，通常被称为学习偏好。学习偏好是指个体应对不同学习任务的方式（ Cassidy，2004）。这些偏好能够提供结构化的支持，同时也具有足够的灵活性，允许个体表现出响应性或适应性行为。简单来说，学习偏好就是选择一种方式而非另一种方式。因此，这些偏好可能会影响学生的学习过程和/或感知能力（Asfani等人，2016）。Lau和Yuen（2009）发现，学习偏好也与编程表现相关，其中反思型学习者的表现优于主动型学习者，而言语型学习者的表现优于视觉型学习者。

机器人课程成果

实证研究表明，愉悦感与自我决定理论中的基本需求之间存在关联。例如，坦博里尼等人（2010）的研究表明，自主性、能力和关联性的满足不仅与愉悦感相关，而且能够解释相当大比例的变异。基于他们的研究结果，坦博里尼等人将愉悦感广义地定义为内在需求的满足。除非活动令人感到愉悦，否则动机和坚持性不太可能出现（拉姆比，2011）。综上所述，游戏愉悦感在成就中起着至关重要的作用，因为它可以促使玩家学习并掌握游戏（桑索内和哈拉奇维茨，2000），而缺乏愉悦感或感到无聊则可能导致学习上的脱离和/或失败（谢尔诺夫等人，2003）。

在机器人技术课堂中，学生在问题解决方面的得分通常更高（巴拉克和扎多克，2009； 弗劳尔斯和戈塞特，2002；奥尔蒂斯等人，2015；泰勒和白，2018；特纳和希尔，2007）。

他们还通过学习编程来提升计算思维技能。G.Chen等（2017）组织了一个围绕特定主题的机器人课程，

4 教育计算研究杂志0(0)

该课程涵盖控制基本运动、语音识别、触觉传感器以及各种其他与机器人技术相关的技能和任务。年仅四岁的儿童就可以通过组装和编程来学习计算思维概念和机器人技术（格罗弗和皮亚，2013）。埃尔金等人（2014）实施了一项机器人课程，将其融入一个混合年龄的蒙台梭利教室的社会科学单元中。本研究是一个将机器人技术独特地用作丰富儿童学习经历的工具的示例，同时仍然实现编程技能的掌握并发展计算思维技能。

感知能力是一种成就信念，也受到了广泛关注。动机研究从不同角度探讨了能力问题，无论是希望变得有能力、表现得有能力、感觉有能力，还是避免在他人面前显得无能（乌尔丹和特纳，2005）。在一项关于与机器人协作的研究中，坦南特等人（2017）发现，当机器人与人类互动时，工人的感知能力会提升。在进行机器人编程时，学生通常有机会通过迭代（反复尝试）、调试（错误解决）以及反馈来发展自身的能力。因此，当学生将自己的成功和成就归因于自身的努力和技能时，他们便能够发展出感知能力（克里姆特， 2003）。然而，尽管先前的研究表明与计算思维相关的诸多益处，但以往的研究尚未全面考察学习过程中的动态变化和/或个体特质。

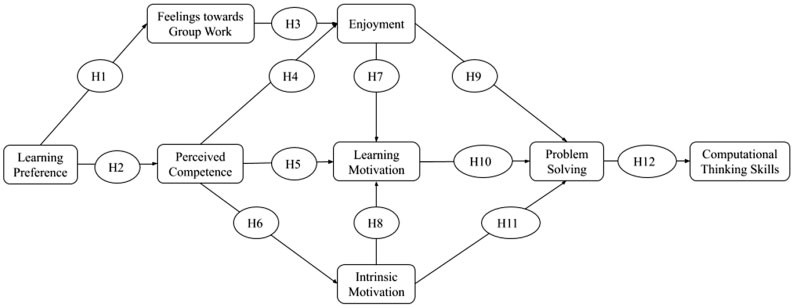
为了探究可能影响学生问题解决和计算思维的多个关键因素，本研究基于认知评价理论（德西和瑞安，2000；瑞安和德西，2000）、班杜拉的社会认知理论（切尔沃内等人，2001）以及哈特的胜任动机理论（霍恩，2014），构建了一个概念模型并提出研究假设。本研究通过整合以往研究中独立探讨的关键因素——包括学习风格、对小组工作的感受、感知能力、学习动机、内在动机和问题解决——为协作机器人环境下的计算思维研究做出了贡献。在协作机器人环境中，这些变量之间的相互作用可能表现为：学生偏好的学习方式积极影响其在搭建和/或编程机器人方面的感知能力，进而使其更愿意在小组合作中承担领导角色等。因此，这些变量之间的相互作用也可能提升他们进行编程以实现机器人预期操作所必需的计算思维技能。简而言之，确定此类关系是否存在，可以为学生学习、课程设计和活动设计提供蓝图，以便充分利用协作机器人背景下的任何积极效应。因此，本研究围绕以下研究问题展开：

RQ1：哪些因素影响小学生在协作机器人中的计算思维技能？

斯图尔特等人 5

文献综述

自我决定理论（SDT）（德西和瑞安，2000）中包含的一个嵌入式理论是认知评价理论（CET），该理论认为存在一些事件和条件能够促进个体对能力感和自主性的感知。这会增强他们在特定活动中的内在动机，因为较低的自主性或能力感会降低内在动机（瑞安等人，2006）。CET的基本观点是，自主支持会影响感知能力的变化，进而影响内在动机（盖等人，2001）。在包含机器人技术的游戏情境中，内在动机是教育的核心（卡洛蒂‐哈拉克等人，2015）。事实上，与其他许多活动不同，玩机器人不仅是一种具有内在动机的活动，还能为学生提供满足某些心理需求的机会（安瓦尔等人，2019）。

此外，已有研究提出，与受外在动机驱动的个体相比，具有内在动机的个体在从事某项活动时通常会获得更多的乐趣（瑞安和德西，2000）。基于这一逻辑推理，可以合理推测参与机器人活动的学生也在寻求内在的满足感。而这种满足感可能与个体的感知能力相关，感知能力常被与自我效能互换使用。根据罗杰斯等人（2014）的观点，感知能力和自我效能均能促进目标追求，并推动学习、行为投入和技能发展。在SDT中，感知能力被认为与任务效能密切相关（罗杰斯等人，2014）。也就是说，能力不仅涉及个体完成任务的能力，还包括其对任务重要性的个人评估。总体而言，自我效能被认为主要涉及能力方面的认知感知（休斯等人，2011）。在本研究中，为了保持一致性，我们将该构念称为感知能力。

个体特征与机器人技术

学生从小学阶段就开始形成对各个学科/内容领域的态度（金德，2017）。为了向所有学生推广计算机科学和编程的可能性，在早期教授这些概念可以使学生了解机器人技术的内涵以及未来可能的发展方向（例如在机器人技术和 STEM相关领域中的职业），否则这些信息可能不为他们所知（贝克和图阿蒂， 2017）。此外，STEM领域较晚引入的另一个问题是，由于缺乏必要的背景知识、动机或其他相关技能，后期进入或转换职业领域可能会变得极其困难（兰姆等人，2015）。教育机器人的目标是促进学生操作机器人所需的分析能力与态度，同时也能让学生更早并以不同的方式学习相关的STEM学科。

6 教育计算研究杂志0(0)

教育机器人通过机器人创建、设计、组装和操作，增强并支持学生的认知技能，同时发展他们的知识内容。

学习偏好、对小组工作的感受和愉悦感。哈达德和卡拉尼（2015）指出，如果计算思维的教学能够根据学生的学习偏好进行调整，那么更多学生将表现更好，并能更有效地掌握所教授的概念。一般来说，学习偏好在很大程度上决定了学习者选择的学习方式最终的效率和/或有效性。例如，一些学习者可能发现小组学习比单独学习更有帮助，而偏好小组学习的学习者可能对小组合作持有更积极的感受。因此，我们提出假设：

假设1：学生的学习偏好将预测其对小组工作的感受。

H2：学生的学习偏好将预测其感知能力。

学习偏好与感知能力

协作或小组工作被广泛定义为一种特定的互动形式，促使参与者共同完成任务（贝克和图阿蒂，2017）。先前的研究已探讨了协作与学习愉悦感在不同情境下的关系，例如数学（舒卡洛等，2012）或机器人教育（Somyu¨ rek,2014）。其他研究结果也表明这两个变量之间存在正向关系。然而，很少有研究探讨学生对协作的感知与其学习愉悦感之间的关系，或得出积极结果的研究较少（鲍威尔和威默，2016）。鲍威尔和威默（2016）的研究是在一门实践性编程课程中进行的，旨在理解学生对小组合作有效性的感知与学习愉悦感之间的关系。因此，我们提出假设：

假设3：学生对小组合作的感受将预测其愉悦感。

个体特征与计算思维技能

感知能力与愉悦感

能力，被描述为对挑战的需求或效能感（德西和莫勒， 2005），也是能力动机理论的核心内容（加斯金，2013）。该理论认为，成功掌握特定技能的经历会增强个体的感知能力，从而进一步提升内在动机。具有内在动机的个体会自然地渴望持续参与

斯图尔特等人 7

活动。尽管已有研究强调积极情感能够提高人们对中等趣味性活动的兴趣和愉悦感（伊森和里夫，2005），但先前的研究已表明感知能力与愉悦感呈正相关。例如，在一项涉及小学生的实证研究中，发现儿童在体育教育中的感知能力与愉悦感之间存在显著的正向关系（卡罗尔和卢米迪斯，2001）。弗尔克拉夫（2003）的一项类似研究也发现，中学生对体育活动的感知能力与愉悦感呈正相关。与本研究更为相关的是，瑞安等人（2006）调查了本科生在一款商业平台游戏中对游戏内能力感知和自主性的感受，发现这两种心理需求与游戏愉悦感显著相关。因此，我们提出假设：

假设4：学生的感知能力将预测其愉悦感。

感知能力、学习动机和内在动机

现有文献强调并证实了内在动机对学习的重要性（例如，格兰特，2008；帕塔尔等人，2008）。例如，帕塔尔等人（ 2008）得出结论，内在动机与高水平的努力和任务表现密切相关。具有更高水平内在动机的学生通常表现出更强的学习坚持性，表现更出色，在学校取得更高的成绩，并且总体上更具生产力（格兰特，2008）。

奥古斯蒂尼亚克等人，2016对医学生的内在动机水平进行了研究，使用了“内在动机量表”，其中感知能力被理论化为内在动机的预测因子和测量指标之一。布莱恩等人，2019类似地考察了视障儿童和青少年自主动机的预测因子，发现感知运动能力能够显著预测自主动机。在另一项研究中，李等人， 2005调查了特质性能力观念、内在动机、感知能力、经验、坚持性和表现之间的关系，研究对象为98名运动学大学生，结果发现感知能力是内在动机的积极预测因子之一。

几项先前的开创性研究为感知能力与动机发展之间的积极关系的存在奠定了坚实的基础（例如，瑞安和德西，2000a，2000b）。基于这些研究，我们提出假设：

H5：学生的感知能力将预测学习动机。

H6：学生的感知能力将预测内在动机。

8 教育计算研究杂志0(0)

其他研究也表明愉悦感是决定学习成果的关键因素之一（例如，布伦斯登等人，2003；戈麦斯等人，2010）。与愉悦感类似，学习动机也是学习过程中另一个在现有文献中被广泛记录的关键因素。多项研究发现其对学习成果具有重要意义（例如，戈麦斯等人，2010；泰拉，2007）。然而，仅有少数研究探讨了学习愉悦感与动机之间的关系，且均表明这两个重要的学习相关因素之间存在正向关系。例如，西尔曼和库楚克（2019）调查了一些职前教师在教育机器人课程中的看法和经验，发现愉悦感与动机之间密切相关。在另一项与本研究密切相关的研究中，哈帕萨洛和塞缪尔斯（2011）认为，通过机器人技术在数学教育中带来的愉悦感可以提高学生的学习动机。因此，我们提出假设：

假设7：学生的enjoyment（愉悦感）能够预测学习动机。

假设8：学生的内在动机会预测学习动机。

如将在下一部分关于假设8的讨论中所述，我们还提出了以下假设：

假设10：学生的学习动机会预测问题解决。

假设H11：学生的内在动机能够预测问题解决能力

悦悦感、学习动机、内在动机和问题解决

在教育领域，大量研究关注问题解决（Karatas&Erden,2017；宋和格拉科夫斯基，2006），因为这是学生必须掌握的最重要的学习技能之一。Baars 等人（2017）认为自主动机可以促进自我调节学习技能的使用，Pekrun等人 （2002）发现内在动机与愉悦感、希望和自豪等积极情感相关。研究表明，学生问题解决能力的发展需要任务坚持性（J~ogi&Kikas,2016）。其他研究也表明，动机水平较高的学生通常更具坚持性（例如，Hardre&Reeve, 2003），这表明有动机的学生更有可能展现出更强的问题解决能力。因此，我们提出假设：

假设9：学生的愉悦感将预测问题解决。

假设10：学生的学习动机会预测问题解决。

斯图尔特等人 9

许多研究已经证明了内在动机对学习的重要性（例如，格兰特，2008；帕塔尔等人，2008）。例如，帕塔尔等人（2008）发现，内在动机与高水平的努力和任务表现密切相关。问题解决技能被视为学生最重要的学习技能之一，因为他们很可能在日常实践中需要解决结构不良的问题（宋和格拉科夫斯基， 2006）。这一点在机器人教育中尤为明显，因为学生需要通过问题解决来找到应对特定设计挑战的解决方案。然而，很少有研究探讨在机器人教育背景下内在动机与问题解决之间的关系。赵和林（2010）的一项涉及一些具有科学天赋学生的研究所发现，学生的内在动机可以预测他们的创造性问题解决技能。

值得注意的是，尽管赵和林（2010）的研究是在数学和科学背景下进行的，而非机器人技术领域，但这两个情境非常接近。因此，我们提出如下假设：

假设H11：学生的内在动机能够预测问题解决能力

计算思维技能与问题解决技能

巴尔等人（2011）提出，计算思维是一组独特的认知技能的结合，能够实现一种新颖的问题解决形式。这一过程还与各种工具（如计算机、机器人）密切相关，可使问题解决的某些方面（如测试、迭代）对学习者而言更加易于获取。

尽管对于构成计算思维（或构成计算思维所必需的最低限度）的具体子技能尚无共识，但计算思维的定义所涵盖的技能范围广泛，包括抽象、系统性信息处理、符号系统与表征，以及流程与控制等算法概念（格罗弗和皮亚，2013）。

自温（2006）的开创性论文以来，计算思维的定义和概念化持续发展演进。

计算思维中的问题解决是指通过使用各种计算模型，运用逻辑思维来解决问题。这包括应用问题分解以识别问题和/或生成问题的替代表示。在这一分析层次上，学生能够区分问题，并判断这些问题是否可以通过计算方法解决。

此外，学生能够评估问题并明确适当的标准，以形成适用的抽象。为了解决问题，学生需要运用计算思维技能中的多个重要组成部分（例如，抽象）。因此，我们提出假设：

假设H12：学生的问题解决能力能够预测计算思维

10 教育计算研究杂志0(0)

材料与方法

本研究的目的有两个：a）探讨某些因素——例如学习偏好、感知能力、学习动机、愉悦感和内在动机——如何预测问题解决能力；b）探究问题解决与计算思维技能之间的关系。假设模型基于12个假设构建而成。首先，本研究试图探讨学习偏好作为对小组合作的态度和感知能力的预测因子的作用。由于学习偏好代表了学生在学习方式上的个体差异，因此本研究假设具有不同学习偏好的参与者会对小组合作产生不同的感受，并表现出不同的感知能力。愉悦感被预测与对小组合作的态度和感知能力相关联。感知能力被认为会影响愉悦感、学习动机和内在动机。此外，愉悦感、学习动机和内在动机被视为预测问题解决的独立变量。最后，研究人员将问题解决引入作为计算思维技能的预测因子，以探索这两个变量之间是否存在直接关联。

提出的模型

基于假设的关系，构建了以下模型以说明所研究变量之间的假设关联。首先，学习偏好预计与感知能力正相关，而感知能力又预计会影响愉悦感、学习动机和内在动机。最后，提出的模型预测问题解决将直接影响计算思维能力这一最终结果（见图1）。

假设1：学生的学习偏好将预测其对小组工作的感受。

H2：学生的学习偏好将预测其感知能力。

假设3：学生对小组合作的感受将预测其愉悦感。

假设4：学生的感知能力将预测其愉悦感。

假设5：学生的感知能力将预测其学习动机。

假设6：学生的感知能力将预测其内在动机。

假设7：学生的enjoyment（愉悦感）将预测学习动机。

假设8：学生的内在动机将预测学习动机。

假设H9：学生的enjoyment（愉悦感）能够预测问题解决能力。

假设H10：学生的学习动机能够预测问题解决能力。

假设H11：学生的内在动机能够预测问题解决能力。

假设H12：学生的问题解决能力能够预测计算思维。

参与者

本研究的参与者来自美国爱达荷州一所郊区学校的四个四年级班级和三个五年级班级。学生的年龄范围为9到11岁。按年级水平和性别划分的学生分布情况见表1。

本研究中的四、五年级学生每周参加一节时长为一小时的工程课。本研究中的大多数学生从幼儿园起就一直参与工程课。工程教师已经

表1. 参与者性别与年级水平的交叉表。
年级水平	性别
	Male	女性
四年级（4个班级）	45(48%)	49(52%)
五年级(3个班级)	49(43%)	65(57%)
总共7个班级(n¼ 208)	94(45%)	114(55%)

12 教育计算研究杂志0(0)

从2017年起教授机器人技术，自2018年起在工程教室授课，并且也作为研究人员参与了本研究。

在研究开始之前，已获得校长和学区管理员的许可。批准内容包括向参加机器人技术课程的学生家长发放知情同意书。研究人员向所有学生说明了研究目的，强调该过程是教师和研究人员的学习经历，而非对学生能力的评估。学生的身份通过编码系统加以保护，确保数据集中的匿名性。

程序

本研究共有38个小组，每组三名学生。小组成员按男生和女生随机配对，所有学生小组在三个月期间协作完成本研究。学生在每节课程期间与同一同伴合作，共享一个机器人。每个小组的任务是共同使用Cþþ编程语言为Botball 机器人编写程序，并完成一系列难度逐渐增加的编程挑战，这些挑战贯穿整个课程。学生小组学习了各种电机、伺服电机和传感器功能的编程。

在小组中，参与者首先学习如何注销学校的Wi‐Fi网络，并改用Wi‐Fi连接Botball机器人。随后，他们学习了如何编写用于伺服电机（机械臂和夹爪控制）和传感器（如光、声音）功能的代码。每个学生小组接着开始使用基本电机功能（方向移动）代码对Botball机器人进行编程。各组被要求挑战编写使机器人前进的代码：motor(0,100);motor(3,100);msleep(2000)。机器人使用0号和3号端口连接电机。

当学生完成这一基础挑战后，他们被赋予了逐步增加难度的更复杂挑战。

例如，下一个任务是编写程序让机器人向前移动并触碰一个铝罐。随后，学生需要编写程序让机器人向前移动、触碰铝罐，然后返回起始位置。学生小组接着使用基本电机功能，操控Botball机器人绕铝罐运动，其难度从沿直线移动逐渐提升到围绕两个铝罐按8字形移动。在完成这些基本电机功能挑战后，他们开始学习使用伺服电机。在学生小组完成伺服电机相关挑战后，他们开始接触传感器。尽管Botball机器人配备了五种传感器，但学生仅被教授了红外 （IR）传感器的功能。红外（IR）传感器的作用是完成一项挑战，即让机器人追踪一条移动的黑线。并非所有学生都能达到这一挑战阶段。

斯图尔特等人 13

每个编程挑战的共同环节是编译代码。如果编程有误，将会出现错误信息。

随后，学生会回头检查代码以查找并纠正错误。随着学生编程技能的提高，学生小组轮流互相帮助编写代码，因为挑战变得越来越困难。这包括使用伺服功能控制机器人的手臂和爪子，以及在为期三个月的单元中学习更多的Cþþ函数。

心理测量特性与数据收集的测量

为了测量假设的心理测量特性，本研究使用了以下问卷：1）计算机科学学习动机评估；2）学习风格量表；3）内在动机量表；以及4）愉悦感、感知能力、问题解决量表和计算思维测试。工程教师（同时也是研究人员之一）在干预前实施了调查，但问题解决量表和计算思维测试除外，这两项在干预后进行。

学习偏好量表

本研究采用了达夫（2004）开发的学习风格量表。该量表包含两个构念：具体性与抽象性，以及反思与行动。第一个构念包含七个题项，每个题项为六点李克特量表，形成从具体到抽象的范围。得分越高，表示越倾向于抽象。第二个构念“反思与行动”包含七个六点李克特量表题项，得分越高，表示从反思趋向行动。该量表的两个构念与学业成就呈正向强相关，表明最有效的学习者往往更强调抽象概念化和主动实践。达夫（2004）得出结论，这十四个题项的量表是测量学习偏好的有效且有用的工具。在术语方面，作者承认文献中关于“学习风格”的实证证据不足（参见基尔希纳，2017）；但我们指出，此处的术语（即“风格”）是按达夫原文保留的。在本文中，我们有意使用“学习偏好”一词，以描述一种可选择的互动模式。

对小组合作的态度

对小组工作的态度通过坎特韦尔和安德鲁斯（2002）开发的“对小组工作感受量表”进行测量。该问卷包含22个李克特项目，采用五点量表，1表示“完全不符合我”，5表示“非常符合我”。该量表涵盖小组合作的五个方面：1）对小组的一般喜好（我喜欢在小组中工作）；2）小组构成（我更喜欢与同性别的成员组成小组进行工作）；3）小组中的自我效能（我感到他人更接纳我）

14 教育计算研究杂志0(0)

在小组合作后）；4）群体动力学（我通常在小组合作中做出强有力的个人贡献）；5）群体组织（小组应自行组织，使工作分配均匀）。与小组合作相关的三个情感领域是“偏好个人工作”、“偏好小组合作”和“在小组工作中感到不适”。

该量表包含来自“偏好个人学习”的七个题项。这些题项用于收集对小组合作强烈不满的看法，包括感觉被小组成员辜负、认为小组合作混乱且不如个人学习有效、更愿意独自工作，以及在小组情境中缺乏参与感和愉悦感。该七题项量表的信度估计值（克朗巴哈系数）为0.78。

该量表包含来自“偏好小组学习”的八个条目。这些条目与在小组学习情境中表现出强烈的投入感和满足感相关——即理解能力增强的感受、乐于分担工作负荷以及共享小组成果的荣誉感、对个人学习贡献的更强感知，以及对小组成员选择的偏好。该八条目量表的信度估计值为0.71。

该量表包含来自“在小组学习中感到不适”的四个项目。这些项目用于测量在小组学习情境中的不适感——包括紧张和无法放松的感觉、害怕寻求帮助以及难以理解小组任务的性质。该四项目量表的信度估计值为0.60。

感知能力

感知能力使用内在动机量表（IMI）中的感知能力子量表进行测量，该量表已用于先前与内在动机相关的研究中（参见瑞安和德西，2000b）。该测量包含六个项目，例如“我认为自己在这项活动中表现相当好”以及一个反向计分项目“这是一项我做得不太好的活动”。每个项目采用七点李克特量表进行评估，范围从1（非常不同意）到7（非常同意）。该量表已被证明具有较高的信度和效度，克朗巴哈系数高达0.80–0.94（崔等人，2009）。

愉悦感

愉悦感的测量采用了方等人（2010）开发的量表。该11项量表包含三个维度，用于测量电脑游戏享受感：情感方面（a¼.73）、认知方面（a¼.77）和行为反应（a¼.83）。该量表的情感方面包含五个题项，其中四个为反向题项，关注游戏过程中的负面情绪（例如：我在玩这个游戏时感到不开心/ 我感到疲惫/我感到担忧/我感到痛苦）。行为方面的三个题项旨在评估玩家的观看意图和

斯图尔特等人 15

行为，而认知方面的另外三个项目则关注游戏过程中对角色行为的判断（方等人， 2010）。

计算机科学学习动机评估

该问卷由劳等人（2010）开发，用于考察影响学生在编程课程中学习的关键动机因素。该测试包含19个项目，分为内在因素和外在因素；内在因素关注个体本身而非环境背景。这些因素通常包括个人态度与期望、挑战性目标（包含情感）。外在因素则源于学习环境之外。影响学生编程动机的六个因素为：‘个人态度与期望（四个项目）’、‘挑战性目标 （三个项目）’、‘明确方向（两个项目）’、‘奖励与认可（三个项目）’、‘惩罚（两个项目）’以及‘社会压力与竞争（四个项目）’。因子载荷的数值验证了所有构念的有效性，除了‘惩罚’中的单个项目。每个构念的区分效度通过多特质矩阵进行检验，范围为.66至.89，显示出各个构念具有较高的效度系数。该测试的克朗巴哈系数为.95（内部一致性水平较高）。

内在动机

本研究采用的内在动机量表改编自哈努斯和福克斯（2015）。该量表包含四个子量表中的七个项目：兴趣/enjoyment、感知选择、感知能力以及压力/ 紧张
行为。IMI量表的项目采用五点李克特量表进行测量，范围从1（非常不同意）到 5（非常同意）。此外，在全部四个子类别中共有10个负向或反向题项：其中兴趣/enjoyment包含两个反向题项，感知选择包含五个反向题项，感知能力包含一个反向题项，压力/紧张包含两个反向题项。IMI量表原本包含45个项目，用于评估用户在七个维度上的经验：兴趣/enjoyment、感知/能力、努力/重要性、压力/紧张、感知选择、价值/有用性以及关联性。哈努斯和福克斯（2015）报告了该22个项目的量表的克朗巴哈系数为.86。

问题解决量表

本研究采用了库尔穆西等人（2016）研究中的问题解决量表（PSI），用于测量个体对自身问题解决能力的认知，以及与问题解决风格相关的行为和态度。该量表包含三个潜在维度：问题解决信心、趋近‐回避风格和个人控制。这些因素不仅相互关联，而且已被证明是不同的维度。第一个因子“问题解决信心”包含11个项目，第二个因子“趋近‐回避风格”包含16个项目，第三个因子“个人控制”包含5个项目。重测信度如下：问题解决信心， r¼.85；趋近‐回避风格，r¼.88；个人控制，r¼.83；总量表为r¼.8。Micoogullari Ekmekci（2018）报告称，在土耳其人群中，各子量表的克朗巴哈系数（a）信度指数如下：解决问题自信度（PSC）为0.69，回应与回避（AA）为0.73，个人控制力（PC）为0.68。黄和Flores（2011）报告称，美国堡姐人样本中 PSI总分的克朗巴哈系数为0.86，PSC为0.77，AAS为0.76，PC为0.66。库尔穆西等人（2016）报告称，解决问题自信度的克朗巴哈系数为0.90，趋近‐回避风格为0.89，个人控制为0.79，PSI总分为0.91。因此，该量表被认为是一种有效且可靠的测量工具。

计算思维能力

计算思维测试（CT‐test）最初由MarcosRoma´nGonza´lez开发，包含40个项目，之后优化为28个项目（CT‐test2.0）。该测试可用作前测，以测量学生初始的计算思维水平，并检测其在编程方面的特殊技能或特殊需求（Roma´n‐Gonza´lez，2015）。根据Roma´ n‐Gonza´ lez等人（2017）的观点，CT‐test的另一个目标是评估学生（K‐5年级和K‐10年级）在计算思维方面的发展水平。

CT测试从五个维度评估用户的计算思维水平：涉及的计算概念、项目的环境‐接口、答案选项风格、嵌套的存在性以及所需任务（Roma´ n‐Gonza´lez 等，2017）。在第一个维度方面，测试包含若干题目，涵盖以下计算概念： 1）基本指令和序列（4个题目）；2）循环‐重复次数（4个题目）；3）循环‐重复至…（4个题目）；4）if‐简单条件（4个题目）；5）if/else‐复杂条件（4个题目）；6）while条件（4个题目）；7）简单函数（4个题目）。所有这些题目按难度递增顺序排列。在第二个维度方面，有23个题目采用“迷宫”环境‐接口，5个题目采用“画布”环境‐接口。这两种接口均常用于编程学习（Roma´n‐Gonza´lez等，2017）。另一个常用于编程学习的特征是使用视觉箭头和视觉块，这些在第三个维度中作为答案选项风格呈现（8个题目使用视觉箭头，20个题目使用视觉块）。关于第四和第五个维度，Roma´n‐Gonza´lez等（2017）指出，有29个题目存在计算概念的嵌套，11个题目不存在嵌套。而所需任务维度则更侧重于认知方面任务，包括排序、一组命令、完成和调试。这些任务在解决与计算思维相关的问题时至关重要。至于CT测试的可靠性， Roma´ n‐Gonza´lez等（2017）报告了28个题目的内部一致性良好（a¼ 0.793）。

结果

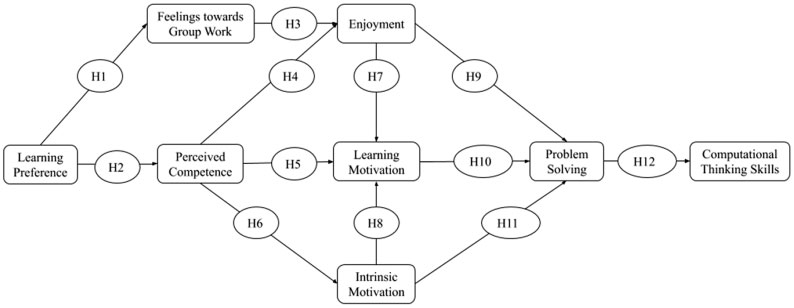
假设模型将愉悦感、学习动机和内在动机预测为问题解决的预测因子。该模型还假设了学习偏好与对小组合作的态度以及感知能力之间可能存在相关性，而感知能力被假设可预测愉悦感、学习动机和内在动机，如图2所示。

表2. 相关矩阵。	1	2	3	4	5	6	7	8
1. 学习偏好	–	.058	.251**	.087	.027	.030	.234**	.092
2. 对小组工作的感受 小组合作	.058	–	.083	.289**	.318**	.100	.026	.039
3. 感知能力	.251**	.083	–	.379**	.358**	.150*	.206**	.182**
4. 愉悦感	.087	.289**	.379**	–	.283**	.124	.195**	.128
5. 学习动机 趋向计算机科学	.027	.318**	.358**	.283**	–	.003	.217**	.181**
6. 内在动机	.030	.100	.150*	.124	.003	–	.005	.059
7. 问题解决	.234**	.026	.206**	.195**	.217**	.005	–	0.601**
8. 计算思维	.092	.039	.182**	.128	.181**	.059	0.601**	–

*p<.05，双尾。**p<0.01，双尾。N¼ 208，CS¼计算机科学。

18 教育计算研究杂志0(0)

学习偏好与对小组合作的态度之间没有显著相关性（相关系数¼0.058， p¼ 0.406）；因此假设1未得到支持。然而，学习偏好与感知能力之间存在显著关系（相关系数¼ 0.251，p< 0.01）。此外，相关性分析结果显示，内在动机与学习动机之间无显著相关性（相关系数¼ 0.003，p¼ 0.965），与问题解决之间也无显著相关性（相关系数¼0.005，p¼ 0.941）。因此，假设8 和假设11未得到支持。如预期所示，相关性结果表明感知能力与愉悦感之间存在显著关系（相关系数¼ 0.379，p< 0.01），与学习动机之间存在显著关系（相关系数¼ 0.358，p< 0.01），以及与内在动机之间存在显著关系（相关系数¼ 0.150，p< 0.05）。此外，相关性结果还显示愉悦感与学习动机之间存在显著关系（相关系数¼ 0.283，p< 0.01）。最后，我们的分析结果显示愉悦感与问题解决之间存在显著关系（相关系数¼ 0.335，p< 0.01），学习动机与问题解决之间也存在显著关系（相关系数¼ 0.335，p< 0.01）。问题解决与计算思维技能之间也发现了显著关联（相关系数¼ 0.441，p< 0.01）。

多元回归

采用线性回归分析检验表3中所有假设预测是否得到支持。回归分析结果表明，学习偏好是感知能力的显著预测因子（R2 ¼.063，F(1,206)¼ 13.881，p<.01）。因此，假设2（即抽象型和行动型学生在感知能力上更高）得到支持。

对小组工作的感受（b¼.260，p<.01）和感知能力（b¼.358，p<.01）是愉悦感的显著预测因子（R2 ¼.211，F(2,205)¼ 14.243，p<.01），这些结果支持了假设3和假设4，即对小组合作感受更积极且感知能力更高的学生具有更高的愉悦感。感知能力（b¼.292，p<.01）和愉悦感（b¼.173，p<.05）是学习动机的显著预测因子（R2 ¼.154，F(2,205)¼ 18.594，p<.01），因此假设5和假设7得到支持，这意味着当学生感知到能力和愉悦感时，他们的学习动机会更强。感知能力也预测了内在动机（R2 ¼.023，F(1,206)¼ 4.752，p<.05），支持了假设6，即学生感知能力越强，其内在动机也越高。

愉悦感（b¼.280，p<.01）和学习动机（b¼.199，p<.01）是问题解决的显著预测因子（R2 ¼.067，F(2,205)¼ 7.308，p<.01），支持了假设9和假设10，即愉悦感和学习动机水平较高的学生在问题解决方面也表现更好。最后，问题解决是计算思维能力的显著预测因子（R2 ¼.361，F[1, 206]¼ 116.406，p<.01，b¼.181，p<.01）。

斯图尔特等人 19

支持假设12，意味着学生在问题解决方面的得分越高，其计算思维技能也越高。

另一项回归分析被用来探究在表4中显著相关的变量之间的关系。首先，以对小组工作的感受作为学习动机的预测因子进行回归分析。表4显示，对小组工作的感受是学习动机的显著预测因子（R2 ¼ 0.101，F[1, 206]¼ 23.220， p< 0.01），该模型解释了9.7%的变异。其次，进行了一项多重回归检验，以探讨问题解决如何由在模型中与问题解决呈正相关的变量所预测。因此，将愉悦感、学习动机、感知能力和学习偏好作为问题解决的预测因子纳入分析。整体模型显著（R2¼ 0.116，F[4, 203]¼ 6.661，p< 0.01），结果表明

表3. 回归分析。	感知能力的预测因子	B	SE	B b	t
	学习偏好	.091	.024	.251**	3.726
	R2	.063	F	13.881**
	享受的预测因素	对小组工作的感受	.176	.042	.260**
		感知能力	.443	.077	.358**
		R2	.211	F	27.355**
	学习动机的预测因素	感知能力	.619	.147	.292**
		愉悦感	.294	.119	.173*
		R2	.154	F	18.594**
	内在动机的预测因子	感知能力	.155	.071	.150*
		R2	.023	F	4.752*
	问题解决的预测因素	愉悦感	.280	.136	.145*
		学习动机（CS）	.199	.080	.176*
		R2	.067	F	7.308**
	计算思维技能的预测因素	问题解决	.181	.017	.601**
		R2	.361	F	116.406**

注：*p<.05，**p<.01，N¼ 208，CS¼计算机科学。

20 教育计算研究杂志0(0)

问题解决能力显著地由两个变量预测：学习偏好（β¼ 0.178，p< 0.01）和面向计算机科学的学习动机（β¼.181，p< 0.05）。第三，进行了一项多重回归检验，以探讨三种与计算思维技能呈正相关的变量如何预测计算思维技能。该整体模型同样显著（R2¼ 0.076，F[3, 204]¼ 5.627，p< 0.01），结果表明感知能力和面向计算机科学的学习动机均不是显著预测因子，而问题解决（β¼.176，p< 0.01）是显著预测因子。

表4. 回归分析。	学习动机的预测因素	B	SE	B b	t
	对小组工作的感受	.367	.076	.318**	4.819
	R2	.101	F	23.220**
	问题解决的预测因素	学习偏好	.178	.080	.145**
		学习动机（CS）	.181	.083	.176*
		R2	.116	F	6.661**
	计算思维技能的预测因素	问题解决	.176	.015	.150**
		R2	.023	F	5.627**

*p<.05，**p<.01，N¼ 208，CS¼计算机科学。

斯图尔特等人 21

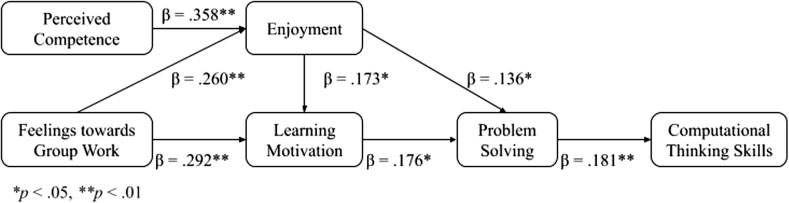
修订后的模型

根据对预测关系的数据分析，我们构建了一个修订模型，该模型还包含了由相关性和回归分析结果支持的未假设关系。如图3所示。

修订后的模型排除了学习偏好和内在动机，因为分析显示问题解决与其他变量之间不存在显著关系。

讨论

假设模型考虑了学习偏好对小组合作感受、感知能力、愉悦感、学习动机、内在动机以及问题解决的影响，我们发现这些关系有的得到支持，有的未得到支持。最终修订模型（图3）展示了这些影响之间的细微差异，我们从单向关系的角度来解释这些关系。例如，尽管研究结果并未提供证据表明学习偏好是计算思维技能的直接预测因子——这与先前的研究一致（如Falvo和Pastore， 2005），但学习偏好被发现与感知能力存在显著关系，并且是感知能力的预测因子。反过来，感知能力和对小组合作的感受成为计算思维技能的决定因素，并与愉悦感、学习动机以及问题解决相关联。问题解决被发现可由两个变量显著预测：学习偏好和对计算机科学的学习动机。因此，尽管在我们的修订模型中，学习偏好可能不是计算思维技能的直接决定因素，但在整体学习环境的考量中仍具有其价值。

这些结果的意义在于，在协作式机器人学习环境中，需要考虑多种心理测量特性，以促进最佳的学习效果，因为某些特质即使不是直接影响，也可能具有顺序上的影响。从实践角度来看，理解学习偏好对感知能力的影响，以及感知能力与内在动机等因素之间的相互关联，有助于课程和学习活动的设计。根据修订后的模型，我们建议应努力培养小学生的感知能力和自信心，使他们在心理上为以计算思维技能为预期成果的协作学习环境做好准备。同样，由于此类学习环境的协作性质要求小组合作与互动，小学生应在教育环境中常规性地接触小组合作，并获得积极的强化。我们发现，对小组工作的感受是学习动机的显著预测因子，这凸显了社会学习的重要性及其激励学生学习的潜力。Y. Chen和Chang（2018）同样发现了STEM融合机器人与学生后续对STEM 整体以及对机器人技术本身的兴趣之间存在积极关系。简而言之，在协作

22 教育计算研究杂志0(0)

机器人技术中存在明确的因素和决定因素，可以从整体角度通过教育干预加以针对性地培养。

结论

本研究揭示了影响协作机器人环境中计算思维技能的多种因素。本研究是首批探讨学习偏好及其对计算思维技能影响的研究之一。尽管学习偏好作为计算思维技能的决定因素未得到支持，但本研究提出了一个修正后的因子模型，其中五个假设关系（感知能力、对小组合作的态度、愉悦感、学习动机、问题解决）被证实对计算思维技能具有显著影响。然而，与其他研究一样，这些发现应谨慎对待，因为存在一些局限性，在考虑这些结果是否适用于其他人群或情境时需要注意。首先，该样本中参与者的总数相对较少，这在一定程度上限制了统计效力。其次，参与者所处的社会文化背景（美国爱达荷州）可能限制了研究结果推广到其他地区不同背景学生时的普适性。尽管如此，这些因素对于课程、活动设计和学习环境设计具有重要意义，其中协作、社会学习和感知能力可能是学生成功的关键。未来的研究可以探索培养学生这些因素的方法，以实现最有效的课程与活动设计，特别是未来研究中双向相关性的潜在作用。

利益冲突声明
作者声明，其在本研究、署名和/或出版方面不存在任何潜在的利益冲突。

资金支持
作者未获得本文研究、撰写和/或发表的任何资金支持。

ORCID iD
威廉·H·斯图尔特 https://orcid.org/0000-0002-8227-849X