并行掩码与有界矩模型

掩码方案的并行实现与有界矩泄漏模型

1 引言

掩码对策是目前为提高针对功耗分析攻击的安全性而研究最多的解决方案[26]。它已在所谓的探测和噪声泄漏模型中进行了理论分析[42,53]，并基于大量案例研究，使用了各种统计工具（例如[16,60]用于非轮廓化和轮廓化攻击，分别对应）。简而言之，目前最先进的掩码方案主要分为两大趋势：一方面，是遵循Prouff和Rivain[56]最初工作的面向软件的掩码；另一方面，是遵循Nikova、Rijmen和Schl¨affer[50]最初工作的面向硬件的掩码（或阈值实现）。

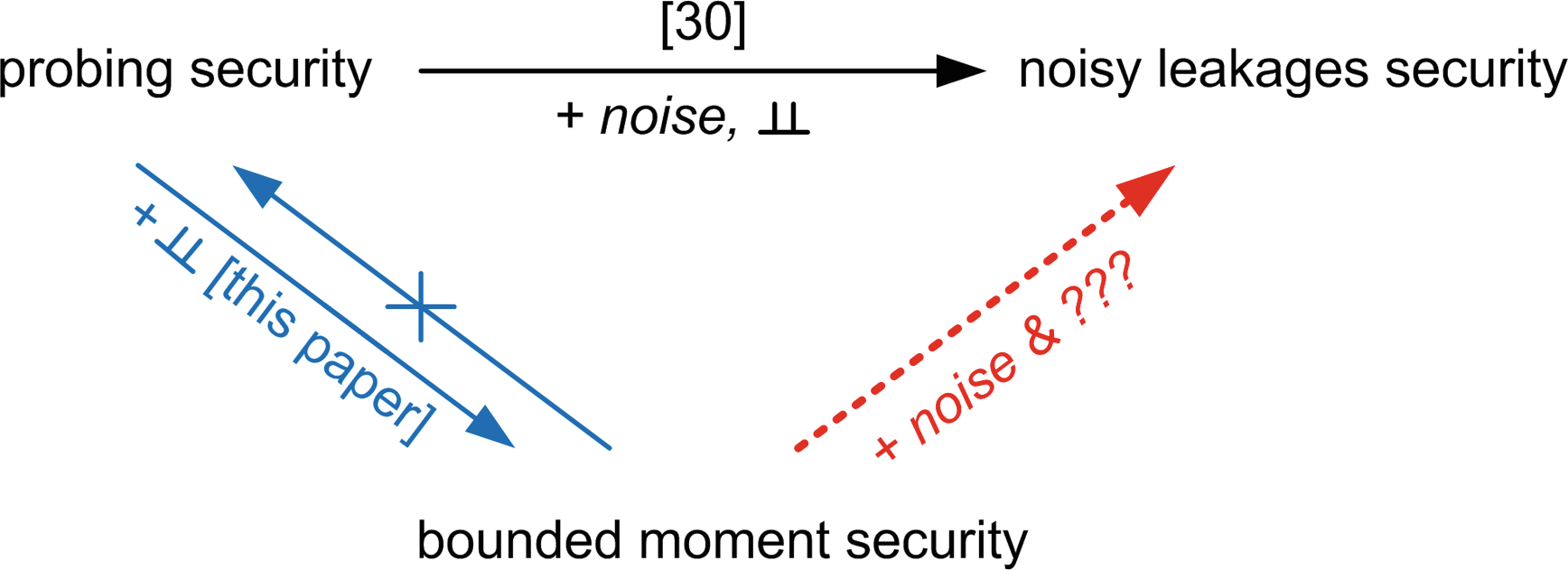
在CRYPTO 2015上，Reparaz等人指出了这两类研究工作中的电路构造之间存在的一些有趣联系[55]。审视这些联系时，面向软件和面向硬件的掩码方案之间仍存在一个明显的差异：前者（的分析）通常假设对份额进行串行操作，而后者（的实现）则鼓励对份额进行并行操作1。遗憾的是，探测泄漏模型虽然有助于准确理解面向软件的掩码方案的安全保证[31]，却无法直接适用于并行环境。直观地说，这是因为份额的并行操作会泄露关于所有份额的信息（例如通过它们的和），但在探测模型中不允许观察线路的和。正如下文将明确指出的，这并不会限制探测模型的实际相关性。然而，它揭示了在串行和并行掩码实现的理论理解水平之间存在差距。

1.1 我们的贡献

从并行性是软件与面向硬件的掩码之间关键差异这一观察出发，我们引入了一种新的模型——有界矩模型，该模型支持对并行掩码实现进行严格推理和高效分析。总之，有界矩模型可被视为在高阶攻击下的安全性的形式化对应概念，正如噪声泄漏模型[53]是信息论泄漏度量（如[59]中所提出的）的形式化对应概念一样。该模型使我们能够扩展[55]的整合性工作，并得到以下结果：

– 首先，我们展示了探测模型与有界矩模型之间的一种自然联系。更准确地说，我们证明了串行实现的探测模型中的安全性意味着相应并行实现的有界矩模型中的安全性。

– 接下来，我们提出适用于并行实现的常规刷新和乘法算法。得益于并行性，这些算法可以在线性时间内实现，且内存需求与串行实现相同（因为掩码本身就需要存储所有份额）。需要注意的是，该刷新算法在与密钥同态原语（例如基于内积的[36]）结合时具有显著优势，因为它能够以线性（时间和随机性）复杂度实现掩码。至于乘法算法，其线性执行时间也有助于提升对多变量（又称横向）侧信道攻击[17]的安全性。

– 第三，我们展示了探测模型与有界矩模型之间的具体分离。为此，我们提供了来自文献中关于信息泄露压缩和低熵掩码方案的简单示例，表明（对于线性泄露函数）在有界矩模型中可能实现比探测模型更高的安全阶数[25,41]。更重要的是，我们证明了我们的简单刷新算法在探测模型下对利用连续泄露的攻击者是不安全的，而在有界矩模型中仍能抵御此类（实际相关）的攻击者。这为一个有用的观察提供了理论基础，即在实践中有时被采用的简单刷新方案（例如添加和为零的份额），尽管在连续探测模型下缺乏安全性，但在用于刷新不可变秘密状态（例如分组密码密钥）时并不会导致灾难性的攻击。请注意，该结果对于串行实现同样具有重要意义。

– 最后，我们通过选择的案例研究来说明我们的结果，并利用这些案例讨论侧信道攻击中独立泄露的假设（及其背后的物理直觉）。

1.2 相关工作

串行掩码与形式化方法。 探测模型的概念简单性使其成为自动化验证的理想目标。Moss、Oswald、Page和Turnstall[49]认识到信息流策略与探测模型中的安全性之间存在密切相似性，因此构建了一个掩码编译器，该编译器以无保护的程序为输入，并输出一个等效但能够抵抗一阶差分功率分析的程序。他们的编译器对输入程序执行基于类型的分析，并在遇到类型错误时迭代地转换程序。为了提高通用性，Bayrak、Regazzoni、Novo和Ienne[18]提出了一种基于SMT的方法，用于分析秘密输入与中间计算之间的统计独立性，仍限于一阶差分功率分析的背景下。Eldib、王和肖蒙从[38],开始的一系列论文中，开发了更强大的基于SMT的方法，用于综合掩码实现或分析现有掩码实现的安全性。他们的方法基于探测模型中任意阶安全性的逻辑刻画。为了避免因考察高阶情况以及探测模型中安全性的逻辑编码所导致的“状态爆炸”问题，他们采用了复杂的增量验证支持方法，即使对于相对较低的阶数也能有效处理。

Eldib和王随后的工作[37]进一步扩展了这一思路，实现了掩码实现的全自动综合。Barthe、Bela¨ıd、Dupressoir、Fouque、Gr´egoire和Strub[13]利用概率信息流策略与关系程序逻辑之间的联系，引入了另一种基于领域特定逻辑的方法，用于证明探测模型中的安全性。与埃尔迪布、王和肖蒙的方法类似，该方法也适用于高阶情况。有趣的是，它在乘法和S盒上能够实际应用于高达四阶的情况。在另一条互补的研究路线中，Bela¨ıd、Benhamouda、 Passelegue、Prouff、Thillard和Vergnaud[19]开发了一种自动化工具，用于发现针对实现的探测攻击，并利用它找到了在2、3和4阶上最优（在随机性复杂度方面）的乘法实现（分别使用2、4和5个随机比特）。他们还提出了一种适用于任意阶的乘法方案，需要 d2 4+ d个随机比特以实现 d阶的安全性。

所有这些工作都集中在探测模型中安全性的通常定义上。相比之下， Barthe, Bela¨ıd, Dupressoir, Fouque 和 Gr´egoire 引入了一种更强的安全性概念，称为强非干涉（即SNI），该概念能够实现对高阶掩码方案的组合验证[14], ，并显著提升对大规模电路（例如完整的算法）进行分析的能力。与探测模型中的其他若干安全性概念类似，强非干涉是定性的，即一个程序要么是安全的，要么是不安全的。跳出定性概念的范畴，Eldib、Wang、Taha 和 Schaumont[39]考虑了（探测）安全性的通常定义的一种定量松弛，并调整其工具以度量实现的定量掩码强度。他们的定义专门针对一阶矩，但其与有界矩模型之间的联系是显而易见的，将他们的工作推广到我们的新模型中将十分有意义。

阈值与并行实现。 Nikova、Rijmen 和 Schl¨affer 的最初动机是观察到，在硬件中实现掩码的安全性具有挑战性，因为毛刺可能导致份额重新组合[45]。他们为防止此问题提出的主要思想是向掩码计算添加非完整性条件（即确保任何组合电路从不将所有份额作为输入）。许多不同的研究已证实了这一额外要求的实际相关性，使其成为硬件掩码的事实标准（参见[20–22,48,52]以获取一些示例）。我们的以下结果特别与阈值实现相关，因为（i）鉴于其针对硬件的特殊性，它们鼓励对份额进行并行操作，（ii）迄今为止它们的大多数安全性评估都是基于我们用有界矩模型形式化的统计矩估计，以及（iii）在[55]中建议并在最近[28]中分析的高阶实现利用了我们在第8.2节中研究的简单刷新方案。

噪声泄漏模型。 注意，[53]中的噪声泄漏模型还提供了一种自然的方式来捕捉并行实现（事实上是一种更通用的方式：见结论中的图7）。然而，当利用上述形式化方法时，该模型并不总是方便的。实际上，这些工具得益于探测模型的简洁性，以便分析复杂的实现，并且很难支持对噪声泄漏的处理。在这方面，有界矩模型可被视为一种有用的中间方案（即可以使用形式化方法高效地验证有界矩安全性，尽管其验证过程自然比探测安全性更慢）。

最终，我们认为从根本上澄清主流（探测和）噪声泄漏模型与基于统计矩估计的具体评估策略之间的联系是十分有意义的。

2 背景

在本节中，我们介绍串行和并行实现的泄漏设置。为了便于阅读，我们对串行和并行计算模型的描述保持非正式，并将其定义推迟到第5节。

2.1 串行实现

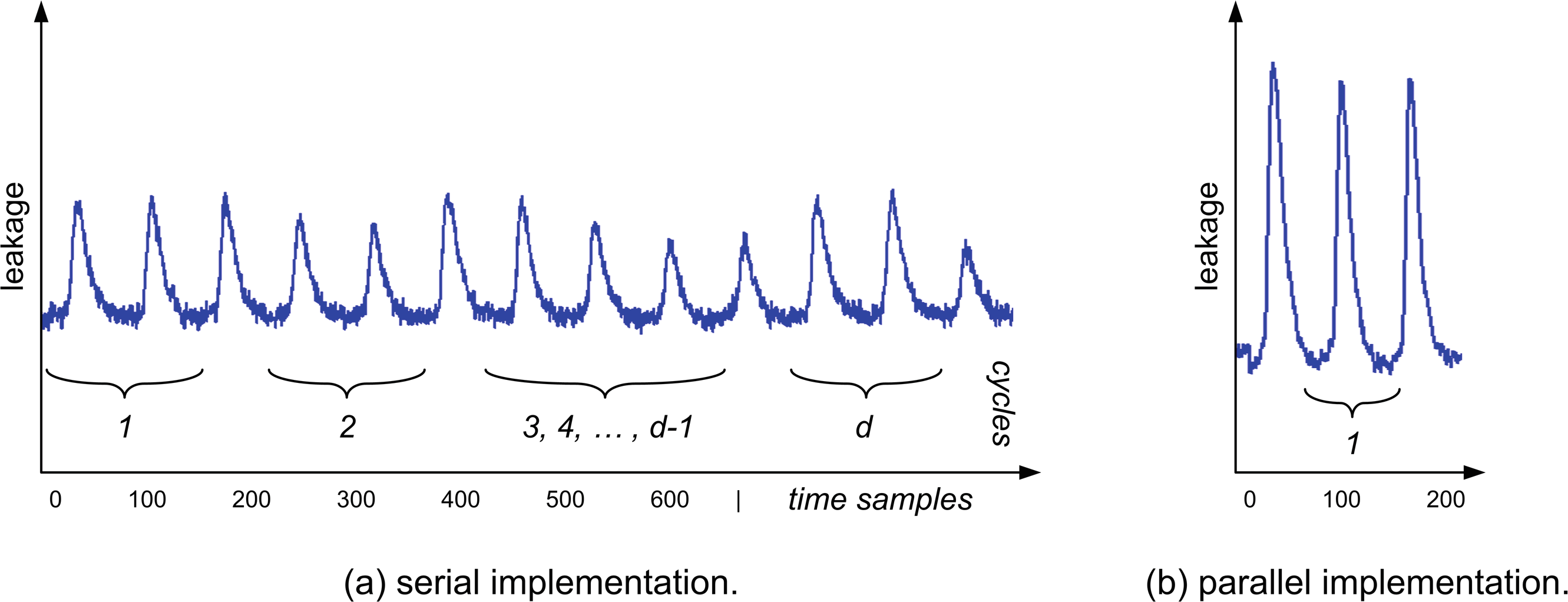
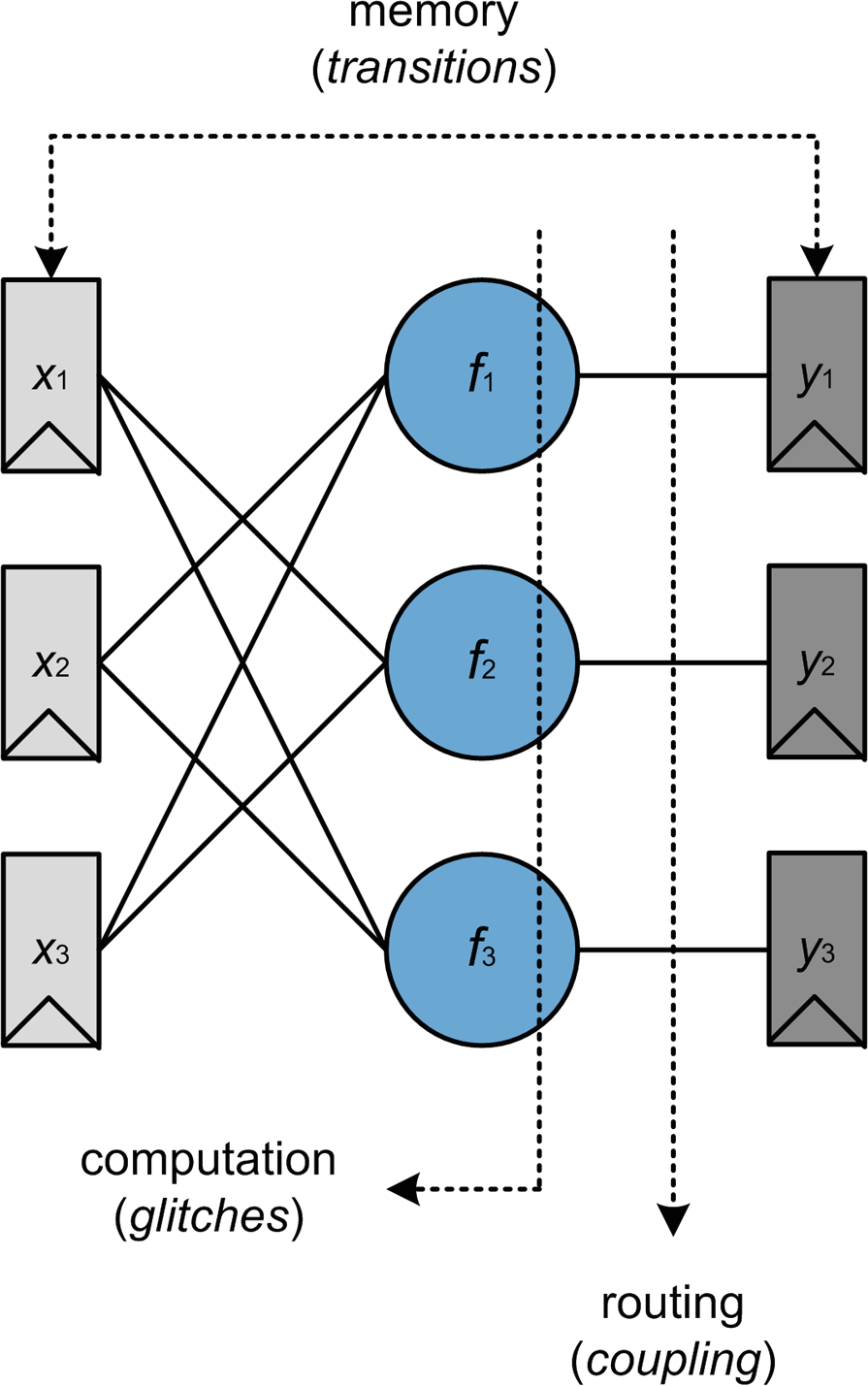
我们从[32],中对泄漏轨迹的描述开始，其中 y是由一个泄漏设备操作的 n位敏感值。通常，它可能是S盒计算的输出，即 y= S(x ⊕ k)，其中 n位明文和密钥字分别为 x和 k。设 y1, y2, . . . , yd为在布尔掩码方案中表示 y的 d个份额（即 y= y1⊕y2⊕…⊕yd）。在侧信道攻击中，攻击者会获得关于每个份额的一些信息（或泄漏）。具体而言，所获得信息的类型高度依赖于所考虑的实现类型。例如，在串行实现中，通常每个份额在不同的“周期” c内被处理，因此实现中的周期数等于份额数量，如图1(a)所示。每个周期中的泄漏表现为一个随机变量 Lc，它是泄漏函数Lc的输出，该函数以 yc和噪声变量 Rc作为输入参数：

Lc= Lc(yc, Rc), with 1 ≤ c ≤ d. (1)

也就是说，每个子轨迹 Lc 是一个向量，其元素表示时间样本。在访问单个样本 τ 时，我们使用符号 Lτ c= Lτ c(yc, Rc)。从这一通用设定出发，侧信道密码分析领域的文献中经常采用若干假设。我们考虑以下两个假设（也在[32]中被考虑过）。首先，我们假设泄露向量 Lc 是相互独立的随机变量。这是掩码证明成立的严格要求，将在第9节中具体讨论。其次，仅为方便起见，我们假设泄漏函数由确定性部分 Gc(yc)和加性噪声 Rc 组成，使得 Lc= Lc(yc, Rc) ≈ Gc(yc) + Rc。注意，此处的 + 符号表示在 R中的加法（而 ⊕ 表示按位异或）。

2.2 并行实现

我们现在将之前的串行实现推广到并行环境。在这种情况下，主要区别在于可以在同一个周期内操作多个份额。例如，图1的右侧显示了相应的泄漏到一个完全并行的实现，其中所有份额在单个周期内被操作。因此，我们得到一个单一的泄露向量 L1= L(y1, y2…, yd, R1)。更一般地，我们将考虑 N‐周期并行实现，使得对于每个周期 c(1 ≤ c ≤ N)，我们定义在该周期内被操作的份额集合为 Yc，且集合 Yc中份额的数量为 nc。这意味着一个掩码实现至少要求这些集合的并集等于{y1, y2,…, yd}，即所有份额至少被操作一次。这种计算模型是之前模型的推广，因为图左侧的串行实现只需用情况N= d以及对每一个 c, nc= 1来描述即可。如前所述，图右侧的高度并行实现由情况 N= 1和 n1= d来描述。为简便起见，在下文中我们将此情况称为并行实现情况。任何混合串行与并行计算的中间方案（例如每周期2个份额、每周期3个份额等）均可由我们的模型描述。具体而言，并行计算的影响体现在时钟周期数的减少以及瞬时功耗的增加，这在图1(b)中曲线的更高幅度上有所体现。反映这一更高功耗的一个简单抽象如下线性模型：

Lc= α1 c · G1 c(Yc(1))+ α2 c · G2 c(Yc(2))+…+ αn c c(Yc(nc))+ Rc. (2)

包含所有 αj c的 ∈ R。与仅为方便起见使用且在掩码证明中并不需要的加性噪声假设不同，该线性模型是我们对并行实现分析的关键组成部分，因为需要它来维持独立泄露假设。至于可能破坏此假设的其他物理问题，我们假设等式(2)在接下来的章节中成立，并在第9节讨论其可能的局限性。然而，我们已经注意到， 若此假设普遍不成立，则意味着任何以并行方式处理其份额的（例如阈值）实现都应是不安全的。

3 安全模型

3.1 探测安全性与噪声泄漏

We首先回顾两种用于分析掩码对策的重要模型 s.

首先，概念上较为简单的 t-探测和 ε-探测（或随机探测）模型在[42]中被提出。在前一种模型中，攻击者可以获得计算过程中的 t中间值（例如，若我们在二元域中进行计算，则可以探测 t条线路）。在后一种模型中，攻击者以概率 ε获得每个中间值，以概率 1−ε获得 ⊥（其中 ⊥表示无任何知识）。通过使用切尔诺夫界，可以很容易地证明，对于某些 ε的取值， t‐探测模型中的安全性可归约为 ε‐探测模型中的安全性。

其次，噪声泄漏模型描述了许多现实中的侧信道攻击，在这些攻击中，攻击者通过“δ‐噪声”的泄漏函数[53]获取每个中间值的扰动。若对于一个均匀随机变量 Y，泄漏函数L满足SD(Y; Y |LY) ≤ δ，则称其为 δ‐噪声泄漏函数，其中SD表示统计距离。文献[32]表明，一个等价条件是泄漏的信息量不能过大，信息量使用标准的互信息MI(Y; LY)来度量。与 ε‐探测模型不同，攻击者获得的是每个中间变量的噪声泄漏。例如，在掩码的背景下，攻击者可以获得所有份额 Yi的L(Yi, Ri)，这反映了实际实现中攻击者可能观察到所有这些份额的泄漏，因为它们都出现在泄漏轨迹中（如图1所示）。

最近，Duc 等人表明，对探测攻击的安全性意味着对噪声泄漏的安全性[31]。该结果引出了一种自然的策略，即在（更简单的）探测模型中证明安全性，同时基于具体的信息泄漏评估来声明安全级别（如[32]中所讨论的）。

3.2 有界矩模型

动机。 在实践中，探测模型非常适合用于证明第2.1节中串行实现的安全性。这是因为该模型确保攻击者必须通过探测观察到 d个份额才能恢复秘密信息。由于在串行实现中，每个份额在不同的时钟周期内被处理，因此探测点的数量与泄漏轨迹中利用的时钟周期数量之间存在简单的类比关系。相比之下，这种简单类比不再适用于并行实现，因为在并行实现中，给定周期内处理的所有份额可能同时发生泄漏。通常情况下，假设攻击者每次探测只能观察到单个份额，在这种情形下就变得不合常理。例如，更自然的假设是允许攻击者通过一次探测即可观察到公式(2)的输出，这对应于图1(b)中的一个周期，并且已经包含了所有份额的信息（如果 nc= d）。

如引言中所述，噪声泄漏模型为处理并行实现的泄漏提供了一种自然的解决方案。事实上，如果考虑足够大的噪声，则公式(2)的输出仅泄漏有限的信息是完全可能的。然而，直接处理噪声泄漏是在分析掩码实现时，有时会带来不便，例如在使用第1.2节列出的形式化方法进行验证时。鉴于它们在嵌入式安全评估中日益流行，这促使人们迫切需要提出一种替代模型，以支持对并行实现的证明构建，并能通过形式化方法对其进行高效评估。有趣的是，我们将在第5节中证明，该替代模型中的安全性可由探测安全性推导得出。这证实了前述策略的有效性：首先在探测模型中证明安全性，然后基于具体的信息泄漏评估结果来确定安全级别。

定义。 直观上，噪声泄漏模型在形式化方法背景下的主要局限性在于其涉及对完整泄露分布的（昂贵的）操作。在这方面，一种符合实际侧信道文献中所使用的“阶”定义的自然简化方法是将安全性与泄露分布中最小的与密钥相关的统计矩相关联。具体而言，该定义背后的原理在于，掩码实现的安全性源于需要估计更高阶的统计矩，而当各份额的泄漏相互独立且具有足够噪声时，这一任务的难度会随着份额数量呈指数级增长（参见[32]中的讨论）。有趣的是，这样的定义能够直接涵盖并行实现环境，这一点可以通过一个例子轻松说明。

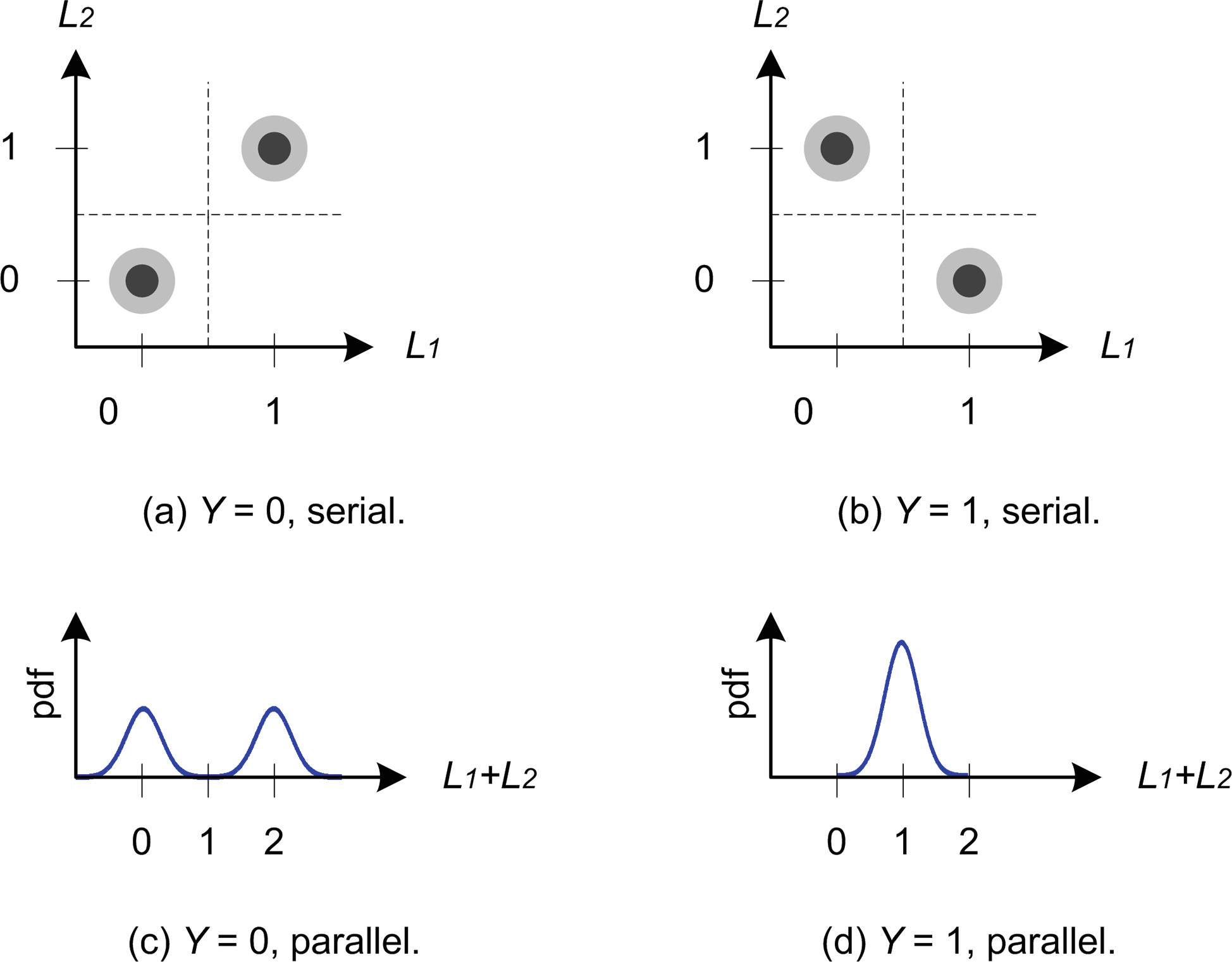
假设我们有一个单比特敏感值 Y被拆分为 d= 2个份额，并且攻击者能够观察到一个泄漏函数，其确定性部分为汉明重量函数，噪声为正态分布。那么，在串行实现中，攻击者可以分别观察两个份额的泄漏，其（双变量）泄漏分布如图2的上半部分所示；而在并行实现中，攻击者只能观察到两个份额泄漏之和，其（单变量）泄漏分布如图下半部分所示。在这两种情况下，泄漏分布的一阶矩（即均值）均与 Y无关。

为了因此，为了定义我们的安全性模型，我们需要以下定义 .

定义1（在阶数 o1, o2, . . . , or下的混合矩）。 设{Xi} r

E(X o1 1 × Xo2 2 ×… × Xo r

其中E表示期望算子， ×表示R中的乘法。为简便起见，我们将整数 o= ∑i oi称为混合矩的阶。进一步地，若恰好有 m个非零系数 oi，则称该阶 o的混合矩为 m-元（或具有维度 m）。

这直接引出了我们在有界矩模型中的安全性定义。

定义2（有界矩模型中的安全性）。 设{Lc} N c=1 为对应于 N-周期密码实现的泄露向量

操作一个秘密变量 Y。如果{Lc} N c=1 的所有阶数不超过 o 的混合矩均与 Y独立，则该实现是在阶数 o上安全的。2

例如，假设我们有一个敏感值 Y，它被拆分为 d= 3个份额，其泄露的含噪声的汉明权重与图2中相同。在（完全）并行实现的情况下，我们只有一个泄露样本 L1，而二阶安全性要求E(L1)和E(L2 1)独立于 Y。在串行实现的情况下，我们有三个样本 L1、 L2、 L3，必须证明E(L1)、E(L2)、E(L3)、E(L2 1)、E(L2 2)、E(L2 3)、E(L1×L2)、E(L1×L3)和E(L2×L3)均独立于 Y。需要注意的是，此示例与具体实现之间的唯一区别在于，在后一种情况下，每个周期对应一个泄露向量 Lc，而不是单个（单变量）样本 Lc。

还需注意，该定义有助于澄清密码硬件社区内关于安全阶数正确定义的长期讨论。即，最初针对安全掩码的定义（在[24]中称为“ o阶完美掩码”，在[30]中称为“ o阶掩码”）专门适用于串行实现，并要求实现中任意 o个中间变量的元组均独立于任何敏感变量。为明确起见，我们现在将这种（强）独立性条件称为“探测模型下 o阶的安全性”。然而，由于该定义专门针对串行实现，因此也引发了关于其推广到并行实现时，是否应关联于最小维度的

2该定义说明了我们为何使用原点矩而非中心矩或标准化矩。事实上，为了在 o阶上建立安全性，我们需要小于o阶的矩与 Y无关。因此，中心化（即减去均值）或通过标准差进行归一化只会引入已知与 Y无关的项。

与密钥相关的泄漏分布（即我们定义中的 m ）或这些分布中与密钥相关矩的最低阶数（即定义中的 o ）。具体而言，在串行实现的情况下为 m ≥ o，但只有第二种方案可推广到并行实现，因为对于此类实现，维度可以低至1，而与份额数量无关。因此，我们在本文其余部分采用此方案，并将这种（较弱的）独立性条件称为“在有界矩模型中 o阶的安全性”。

4 附加特性与讨论

4.1 实验模型验证

很自然地，新泄露模型的引入应伴随经验验证，以证明其合理匹配实际实现及其评估的特殊性。方便的是，在有界矩模型的情况下，我们所做的不过是形式化文献中已部署的评估方法。这一点体现在基于统计矩估计的攻击上，例如利用流行的均值差异和相关性区分器[33,47,57]。这些工具已应用于各种受保护的实现，包括阈值型实现[21,22,48,52]以及其他在近期高频设备上运行的掩码方案或设计[11,12,44]。在所有这些情况下，若发现泄露分布的最低密钥相关统计矩为 o阶，则声称具有 o+ 1阶安全性。

4.2 维度归约

定义2的一个重要性质是，它基于泄露分布的密钥相关矩的统计阶数来刻画安全性。这意味着在有界矩模型中，泄露向量的维度不影响安全阶数。因此，这也意味着此类安全定义不受线性降维的影响。这一简单观察通过以下定义和引理加以形式化。

定义3（线性降维）。 设 L=[L1, L2,…, LM]表示一个 M-样本泄露向量，{αi} m i=1表示 R中的 M-元素向量。我们称 L′=[L′ 1, L′ 2，…， L′ m]为线性缩减的泄露向量，如果其每个（投影后）样本 L′ i对应于一个标量积 〈L;αi〉。

引理1. 设{Lc} N c=1为对应于操作秘密变量 Y的 N-周期密码实现的泄露向量。如果该实现在有界矩模型下在阶数 o是安全的，那么任何对{Lc} N c=1具有线性减少泄漏的实现在阶数 o也是安全的。

证明。 由于 L′的样本是 L的样本的线性组合，我们需要 L′的任意次数不超过 o的多项式的期望独立于 Y。这直接由定义2得出，该定义保证了任意次数不超过 o的单项式的期望独立于 Y。

线性降维的典型示例是PCA[10]和LDA[58]。需要注意的是，虽然线性组合泄露样本不会影响有界矩安全性，但它可用于降低高阶矩计算中隐含的样本噪声，从而可能影响噪声泄漏模型下的安全性。这实际上正是有界矩模型的目标，即通过将评估任务分解为确定性部分（由其矩表示）和概率部分（即噪声）来简化安全性评估。针对侧信道攻击的具体安全性由两个要素保证：高安全阶数和足够的噪声。

4.3 抽象实现设置

在下文中，我们将利用我们的模型来一般性地研究并行性的影响。为此，我们沿用将掩码实现描述为一系列泄漏操作的方法。此外，为了首先抽象掉物理细节，我们考虑所谓的（无噪声的）“抽象实现”，从而将公式(2)简化为：

Lc= α1 · G1(Yc(1))+ α2 · G2(Yc(2))+…+ αnc · Gnc(Yc(nc)). (3)

此类简化使得我们可以独立于具体实现来分析掩码实现，从而检测算法缺陷。请注意，Rc= 0的存在不会影响关于实现安全阶数（在有界矩模型中）的结论，而本文所考虑的唯一度量正是该安全阶数。事实上，该阶数仅取决于泄漏分布中最小的与密钥相关的矩，而与加性噪声无关。相比之下， Rc的方差会影响实现的具体信息泄漏。我们回顾一下，算法上正确的掩码实现并不一定意味着物理安全的实现（例如，由于第9节中讨论的独立性问题或噪声过低）。然而，正如第3.2节所述，在对具体实现进行昂贵的评估之前，测试掩码方案的抽象实现在探测模型或有界矩模型下的安全性是一个有用的初步步骤。

5 串行安全性蕴含并行安全性

我们现在给出在有界矩模型中的第一个结果。具体而言，我们建立了并行实现在有界矩模型中的安全性与串行实在探测模型中的安全性的直观归约关系。为此，我们还形式化了串行和并行计算模型。该归约的一个有用且实际的推论是，人们可以调整现有的工具以证明在有界矩模型中的安全性，方法是实现一个将并行实现转换为串行实现的程序变换，或者将这些工具适配到并行实现。

直觉。 为了对归约提供一些直觉理解，回顾一下抽象并行实现的泄露样本具有如下形式：

Lc= Zc(1)+ Zc(2)+…+ Zc(nc),

其中Zc(i) = αi ·Gi(Zc(i))，且有界矩的形式为：

E(Lo1 1 × Lo2 2 ×… × Lor r).

因此，根据期望的线性性，只要所有形如：的量与秘密无关，则 d阶混合矩与秘密无关

E((Z1(1))o1,1 ×… ×(Z1(n1)) o1,n1 ×(Zr(1))or,1 ×… ×(Zr(nr)) or,nr),(4)

对于所有满足和小于等于 o 的o1,1,… or,nr，它们独立于秘密。注意，至多有 o 个对(i, j)满足oi,j= 0。设(i1, n1), …, (ik, nk)且 k ≤ o 为这些对的一个枚举。因此，为了证明公式(4) 独立于秘密，只需证明元组〈Zi1(n1) …, Zik(nk)〉独立于这些秘密。这实际上恰好对应于在阶数 o 的探测模型中证明安全性。

形式化。 形式化归约的理论框架是一种简单的并行编程语言，其中程序由一系列基本指令组成（注意，添加for循环不会带来额外的困难）。一个基本指令要么是并行赋值：

〈a1,…, an〉:= 〈e1,…, en〉,

其中e1,…, en是由变量、常量和操作符构成的表达式，或为并行采样：

〈a1,…, an〉 ← 〈μ1,…, μn〉,

其中μ1,…, μn是分布。尽管这一形式系统很简单，但它足以用于分析与阈值实现相关的概念，例如非完备性。更重要的是，还可以定义与程序执行相关的泄漏概念。形式上，一个长度为 的程序 c 的执行是一系列状态 s0… s，其中 s0 是初始状态，状态 si+1 由状态 si 按如下方式得到：

– 如果第 i条指令是并行赋值，通过在状态 si下求表达式 e1… en的值得到〈a1,…, an〉:= 〈e1,…, en〉，得到值 v1… vn，并通过将值 v1… vn赋给变量a1… an来更新状态 si； – 如果第 i条指令是并行采样，通过从分布 μ1… μn中采样值得到 〈a1,…, an〉 ← 〈μ1,…, μn〉: v1… vn，并通过将值 v1… vn赋给变量 a1… an来更新状态si。

通过为每次执行分配一个概率（形式上，这是每次随机采样的概率的乘积），可以得到每个程序 c

长度为 的状态分布序列 σ0σ1… σ，其中 σ0是分布 s0。程序的泄漏随后被定义为一个序列 L1… L，通过计算每个 i由第 i条指令赋值的变量所持有的值之和得到，即对于并行赋值（或采样）有 a1+…+ an。在阶数 o下的混合矩直接遵循定义1。对于串行编程语言，指令要么是赋值 a：= e要么是采样 a ← μ。程序的语义定义与并行情况类似。在探测模型中，串行程序的阶 o安全性意味着要证明任意 o个中间值的元组均与秘密独立。

在不失一般性的前提下，我们可以假设并行程序采用静态单赋值形式编写， 即变量满足以下条件：(i)在程序文本中，每个变量仅在赋值或采样的左侧出现一次；(ii)变量在使用前必须先定义（即变量必须先出现在赋值或采样的左侧，然后才能出现在赋值的右侧）；(iii)变量不会同时出现在赋值的左侧和右侧。在此假设下，任何将并行赋值或并行采样转换为赋值序列或采样序列的串行化方法都能保持程序的语义。例如，从左到右串行化将并行指令 〈a1,…, an〉:= 〈e1,…, en〉 和 〈a1,…, an〉 ← 〈μ1,…, μn〉 分别转换为a1:= e1;…; an:= en和 a1 ← μ1;…; an ← μn。

归约定理。 我们现在可以正式陈述该归约： 定理1. 如果一个并行实在探测模型下对阶数 o是安全的，那么它在有界矩模型下对阶数 o也是安全的。

证明 假设一个并行实在有界矩模型中是不安全的，但其串行化在探测模型中是安全的。因此，存在一个混合矩：

E(Lo1 1 × Lo2 2 ×… × Lor r),

即依赖于秘密的。根据泄露向量的定义以及期望的性质，存在程序变量 a1,…, ak，其中 k ≤ o，以及 o′ 1,…, o′ k，其中 ∑i oi ≤ o，使得：

E(a o ′ 1 ′ 2 k)

依赖于秘密，这与以下事实相矛盾：由于在探测模型中串行化的安全性，元组〈a1,…, ak〉 独立于秘密。

请注意，具体而言，该定理提出了高效“组合安全性评估”的可能性，即首先使用形式化验证工具测试探测安全性，若结果为否定，则进一步在（较弱的） 有界矩模型下进行额外测试（参见第8节中的示例）。

有趣的是，它还支持已在 21 中使用的一个结果，其中并未特别讨论实现的并行性，但通常对应于本文中的实验案例研究。

6 并行算法

在本节中，我们描述了用于安全（加法）掩码计算的规则且可并行化的算法。为此，我们将包含 d个份额的向量表示为 a=[a1, a2,…, ad]，将该向量旋转 q个位置表示为rot(a, q)，两个向量之间的按位加法（异或）和乘法（与）操作分别表示为 a⊕ b和 a· b。具体而言，我们的分析聚焦于GF(2)中的计算，但其推广到更大的域是直接的。

6.1 并行刷新

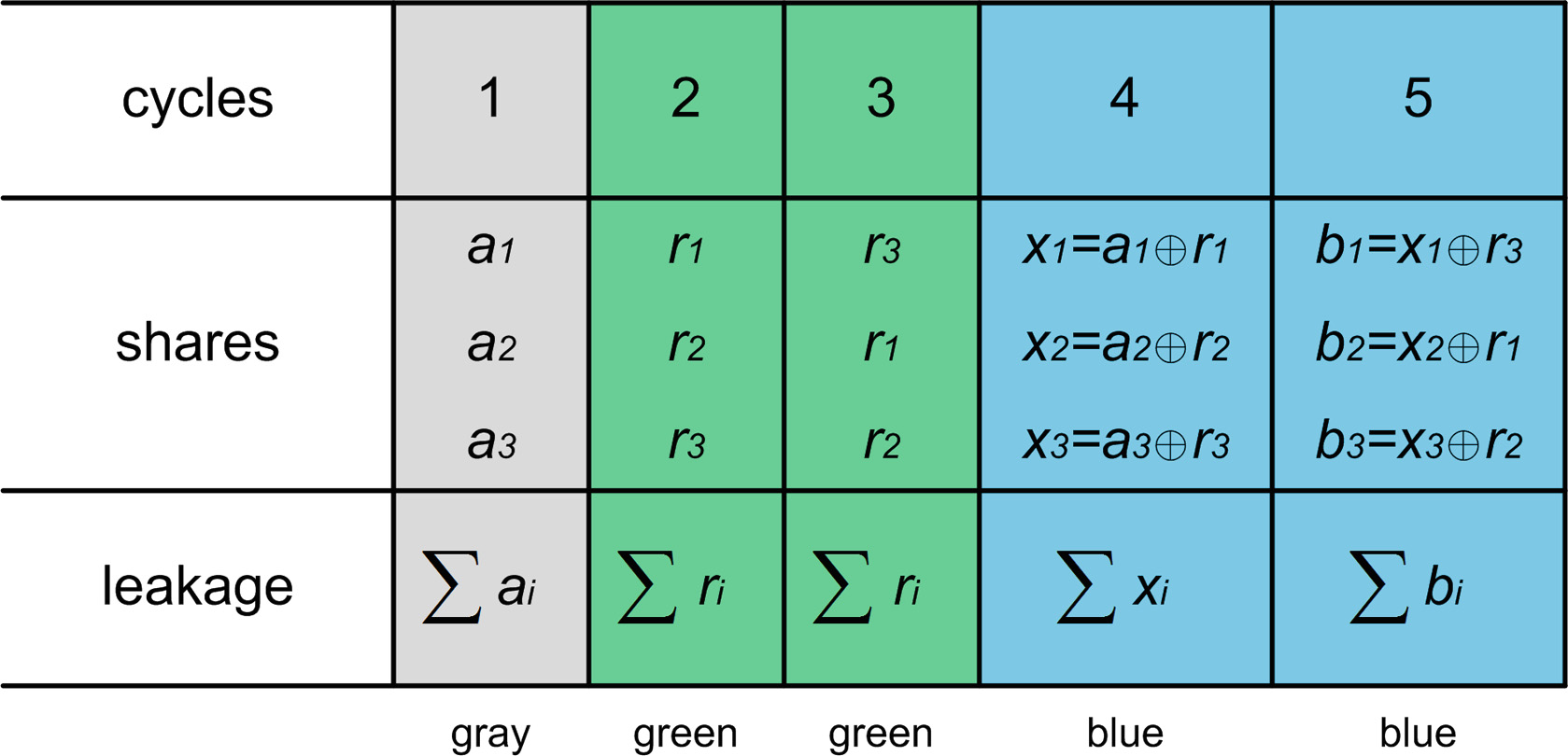
作为起点，我们展示了一种非常简单的刷新算法，该算法在并行实现环境中具有恒定时间复杂度，并且仅需要 d比特的新鲜均匀随机性。该刷新算法如算法 1所示，以及一个抽象示例

算法1. 并行刷新算法。

输入： 满足 ⊕i ai= a, 的均匀随机向量 r的份额 a。

输出： 满足 ⊕i bi= a的刷新份额 b

b= a ⊕ r ⊕ rot(r,1);

返回 b.

6.2 并行乘法

接下来，我们考虑更具挑战性的并行乘法情况，其目标与之前类似，即为屏蔽计算中使用的份额和新鲜随机性提供一种简单且系统化的操作方法。为此，我们的出发点是：现有的安全（串行）乘法（例如[42]（我们将模仿该方法）本质上分为两个步骤：首先是乘积阶段，计算一个 d2元素矩阵，其中包含所有份额的成对乘法；其次是压缩阶段，利用新鲜随机性将这个 d2元素矩阵压缩为一个 d元素的矩阵。因此，给定份额向量 a

掩码方案的并行实现与有界矩泄漏模型

6 并行算法（续）

6.2 并行乘法（续）

并且对两个敏感值 a和 b进行 b操作时，至少可以通过异或和移位操作来执行每一对交叉乘积 ai · bj和 aj · bi，而无需刷新。相比之下，直接乘积 ai·bj必须通过新鲜随机性进行隔离（否则可能在压缩阶段导致对敏感值的操控，例如( ai · bi) ⊕(ai · bj) = ai ·(bi ⊕ bj)）。对于压缩阶段中异或操作之间所使用的均匀随机性，类似的推理也成立。即，每个新鲜向量可以使用两次（以其原始形式和旋转一位后的形式），而不会泄露额外信息。

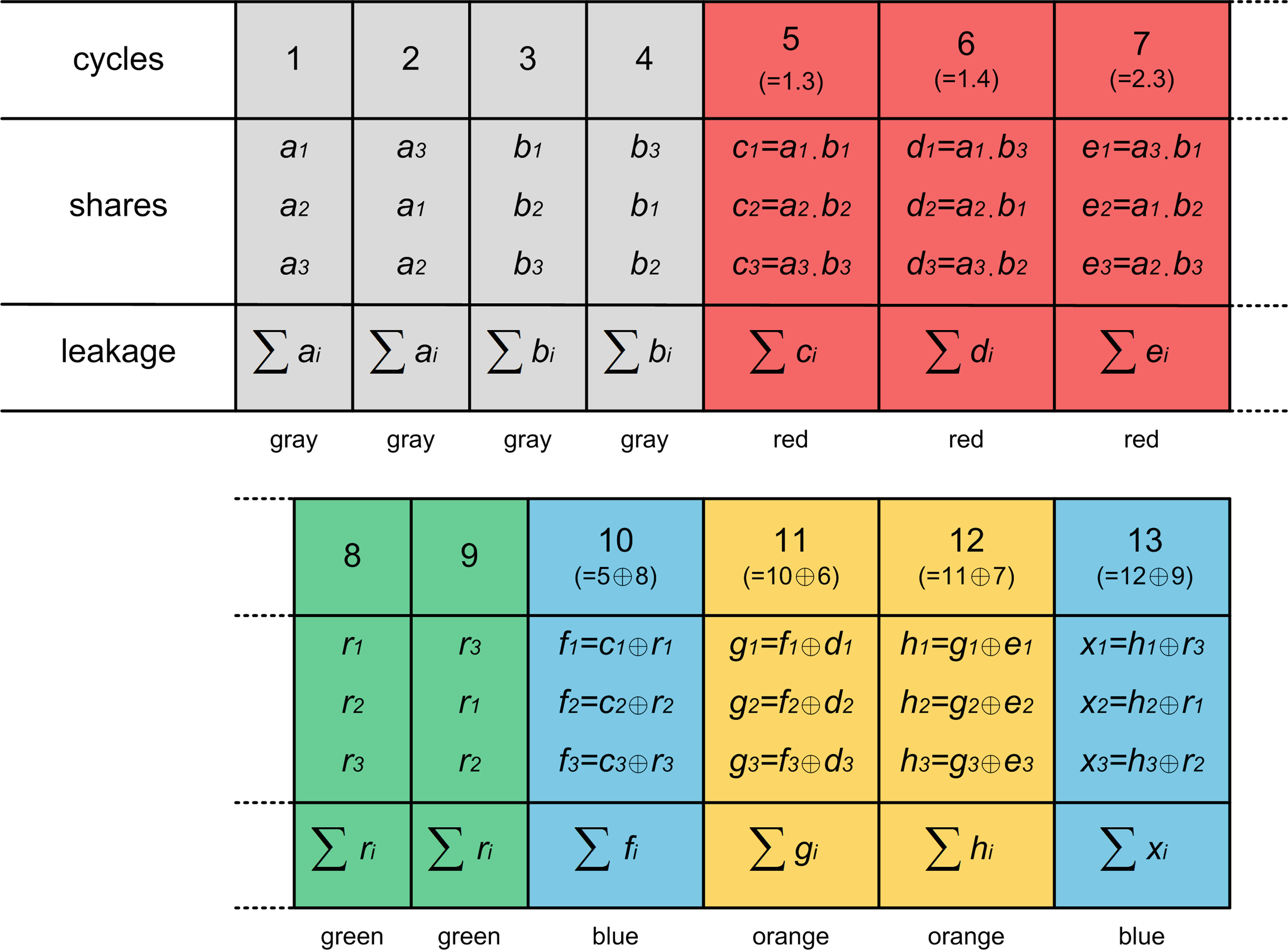
这种思路提出了一种简单的乘法算法，该算法在并行实现环境中具有线性时间复杂度，并需要 ⌈d−1 4 ⌉个长度为 d比特的随机向量（可视为对[19]中算法的一种改进）。我们首先通过图4中其抽象实现来重点说明该算法，该实现以输入共享的加载和旋转开始（灰色周期），然后执行乘积阶段（红色周期），最后通过结合添加新鲜随机性（蓝色周期）与累加（橙色周期）来压缩输出。通常情况下，该实现在 < 5d个时钟周期内完成，适用于 d个份额，具体周期数会根据 d的取值略有变化。

对于 d mod 4= 3 （如图4所示），该过程是“完整”的（即以两个累加周期和一个刷新操作结束）。但对于d mod 4= 0，它以单个累加周期结束；对于 d mod 4= 1，它以两个累加周期结束；而对于 d mod 4= 2，它则以一个累加周期和一次刷新结束。准确的描述见[15],算法3。

对多变量（又称水平）攻击的影响。 简而言之，[31,32]中关于掩码实现的安全证明指出，侧信道攻击的数据复杂度可由1 MI(Yi ,L Y i ) d进行限定，其中 d为份额数量和MI(Yi, LYi)，每个份额的信息泄漏 Yi（为简化起见，假设所有 ∀i相同——否则我们取最坏情况），如果MI(Yi, LYi) ≤ 1 d（其中 d因子是由于[42]的乘法算法中部分积的计算所致）。在最近的一项工作中，Batistello 等人[17]表明，得益于高效的多变量/横向攻击（通过组合对应于同一敏感变量的份额元组，或通过对多次出现的份额进行平均），可以具体利用掩码实现中对份额的操作。有趣的是，尽管在我们的并行情况下也存在多变量/横向攻击的可能性，但并行实现提供给侧信道攻击者的泄露样本数量减少了（大约减少了一个因子 d）， 这也减轻了此类攻击的影响。

7 案例研究

根据定理1，有界矩模型中并行实现的安全性可以通过其在探测模型中的串行化安全性来确立。因此，可以通过将并行实现预处理为串行形式，并将得到的串行程序输入验证工具，利用现有的形式化方法来测试并行实现的安全性。在本节中，我们报告了对多个并行实现的成功自动化分析，包括前一节中提出的并行刷新和乘法，以及并行S盒的串行组合。需要注意的是，由于验证任务的算法复杂性，我们仅在低阶情况下确立了安全性。然而，我们还注意到，尽管我们的主要设计约束是使算法易于并行实现，但通过使用自动化工具（而非手动分析）来验证其安全性，所得到的算法在这些阶数下的随机性要求方面达到或优于最先进的水平。本节报告的所有实验均基于[13]工具的当前版本。该版本支持对两种性质进行自动化验证：通常意义上的探测安全性，以及最近在[14]中引入的、被称为强非干涉（SNI）的严格更强的性质，后者更适用于大规模电路的组合验证。

7.1 并行刷新

We首先考虑上一节中的并行刷新算法。

定理2（算法1的安全性）。 算法1中的刷新在有界矩模型中对于所有 d ≤ 7均在阶 d−1上是安全的。

根据定理1，只需证明(d−1)‐探测安全性，即可在有界矩模型中获得 d−1阶的安全性。我们 使用巴尔特等人[13]提供的工具对每一阶 d ≤ 7进行证明。表1显示了每次证明的验证时间。

此外，我们考虑如何构建一个在并行计算模型下表现良好的SNI掩码刷新小工具。

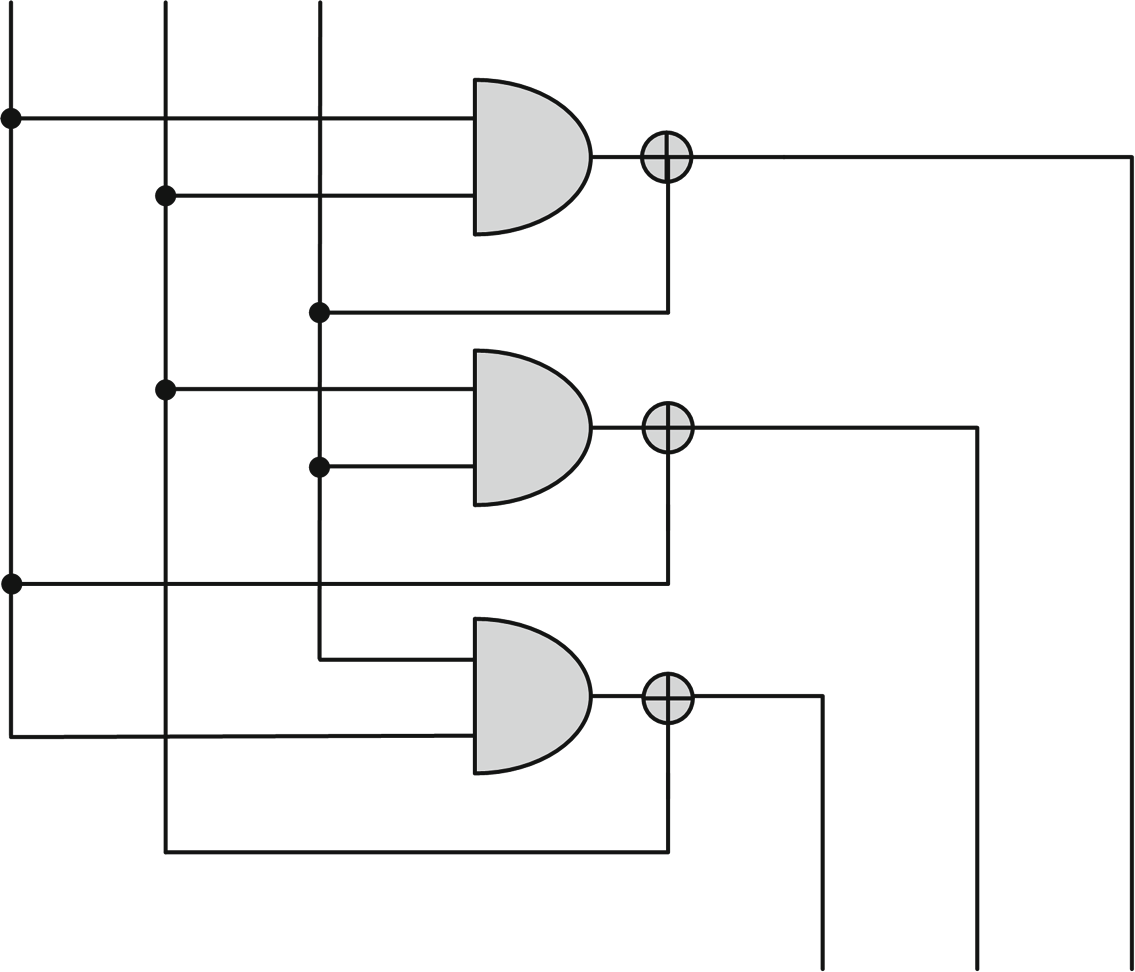
我们依赖巴尔特等人提供的工具的当前版本，[13],该工具支持强非干涉属性的验证。表2报告了若干掩码刷新算法的验证结果，这些算法通过简单地迭代算法1（记为 Rd）构造而成。我们用 Rn d表示迭代 Rd n次的算法。表2还列出了我们的算法以及唯一已知的其他SNI掩码刷新组件的随机性要求，后者基于 伊沙伊、萨哈伊和瓦格纳的乘法算法[42]。

这些实验表明，对于较小的掩码阶数，存在易于并行化的规则掩码刷新小 工具，适用于通过组合方式构建安全电路，并且具有较低的随机性要求。这一 事实通过定理1的视角来看尤为有用。实际上，SNI小工具在轻松证明大规模电 路的探测安全性方面起着关键作用，而定理1 则进一步将其推广到有界矩模型和 并行实现。我们猜想，将算法 1 (d−1)/3中的简单掩码刷新小工具重复迭代 d − 1次，总能得到一个基于 d 个份额的(d − 1)‐SNI 掩码刷新算法。所得到的 算法

很容易并行化，并且需要 (d−1)/3 · d比特的随机性（在ISW‐based mask-refreshing所需的 d ·(d − 1)/2比特随机性基础上略有改进）。我们将其 所有 d的强非干涉证明留作未来工作。

7.2 并行乘法

我们现在考虑上一节中的并行乘法算法（在算法3中指定，见[15]），并证明其对低 阶的安全性。

定理3（算法3在[15]）中的安全性。 [15]中算法3的乘法在有界矩模型中对于 所有d ≤ 7均具有 d − 1阶安全性。

根据定理1，只需证明(d−1)‐探测安全性，即可在有界矩模型中获得 d −1阶的安全性。我们使用巴尔特等人[13]提供的工具对每个 d ≤ 7进行证明。表3显示了每个实例的验证时间。

我们还展示了我们的算法与Bela¨ı 等人[19]的随机性需求的比较。请注意， 与Bela¨ıd 等人[19]的算法相比，我们有时需要多一个随机比特。这是由于我们 的并行化约束：我们不是采样0的均匀共享，而是只允许自己采样均匀随机向量 并对它们进行旋转。

与之前类似，我们现在研究算法1 和 [15]中算法3的某些组合，希望找到规 则且易于并行化的SNI乘法算法。实验结果如表4所示，其中 d是 [15],中 专用于 d份额的算法3。该表除了显示所考虑的算法是否为SNI外，还列出了 验证时间，并将我们的算法的随机性需求与伊沙伊、萨哈伊和瓦格纳的乘法算法进行了比较，后者是目前已知在随机性方面最优的SNI乘法算法。与巴尔特等人[13],的原始工具一样，由于所解决问题的指数性质，验证任务被限制在涉及 单次乘法的电路上的安全阶数 o ≤ 8以内。

我们猜想，对于任意 d，我们的乘法算法与单次刷新的结合都是SNI的。这一 猜想直观上是合理的，因为我们的

乘法算法包含若干“半刷新”，这些半刷新必须与 d的最终刷新相结合，以使 其以累加步骤结束。我们将其猜想的证明作为一个开放问题留待解决。

7.3 S盒和费斯妥网络

为了更好地研究降低乘法和刷新算法的随机性要求对大型电路安全性的影响， 我们现在考虑图5中所示的小型S盒及其迭代。

图5(a) 描述了一个类似于 Ullrich 等人提出的“第13类”S盒的简单 3位S 盒。[62]图5(b) 描述了一个通过对 2位函数 应用 费斯妥结构 构造的 4位S盒。

表5展现了这些电路在多个 低阶 上进行 迭代 的 验证结果，显示出这些阶数下 的一些有趣的 组合性质。sbox3表示图5(a) 中的电路，sbox4表示图5(b) 中的电路，而sboxr4表示该电路

从图5（b）修改而来，使其内部变换的上部输出被刷新。与之前一样，整数指数表示顺 序迭代。

我们注意到，尽管没有证据表明对sbox4进行更多次迭代会产生不安全的电 路，但若不依赖组合原理，使用自动化工具获得超过3次迭代的令人信服的安全 性结果似乎不可行。特别地，每轮Feistel结构中插入一次掩码刷新操作，可显 著加快对图5（b）中4位S盒多次迭代的大规模电路的验证速度。这凸显了面向 特定 d[13,18,38]值的小型优化电路验证工具与面向大规模电路的更高效但精度 较低的验证工具之间的潜在交互作用[14]。使我们的算法具备SNI能力，使我们 能够直接利用这种“随机性复杂度与验证时间”之间的权衡。

8 分离结果

前面的章节说明了，将并行实现在有界矩模型中的安全性归约到其相应串行化 实现在探测模型中的安全性，为安全掩码方案设计中的一系列技术难题提供了 解决方案。现在我们提出一个问题：有界矩模型中所需较弱的安全条件，是否 允许某些实现在该模型中是安全的，而在探测模型中却不安全？我们对此问题 给出了肯定的回答，首先从一些较为特殊但具有说明性的例子开始，然后在连续泄漏的背景下，提出了这两个模型之间一个具有实际意义的分离。

8.1 专用编码和掩码方案

示例开始。 假设一个两周期并行实现，在每个周期中操作两个份额。在第一个 周期中，同一个随机比特 r被加载两次，产生状态（r， r）。在第二个周期中， 一个共享的敏感值a被加载两次，产生状态（a ⊕ r， a ⊕ r）。显然，在探测

模型中，两个探测点（在 r和 a⊕r上）足以学习到 a。但对于观察该并行实现 抽象泄漏的攻击者而言（即每个周期的算术和），以及对于特定类型的泄漏函 数，使得 αj i= 1和 Gj i= Id在公式(2)中成立的情况，第一个周期仅会泄露 r+ r，而第二个周期将泄露常数1。因此，无法通过这些泄漏的任何组合来恢 复 a。一个更简单的例子是 a和 a的并行操作，如果它们的值只是被简单相 加，则显然不会泄露任何信息。此类实现文献中称为“双轨预充电”实现 [61]。其主要问题在于，相比掩码实现，它们需要更强的物理假设。也就是说，关于 份额的泄漏 a和 a不仅需要相互独立，还必须完全相同，这在实际中被证明要 困难得多 [27]。

信息泄露压缩与低熵掩码方案。 有趣的是，文献中提供了其他一些防御措施的 例子，这些措施在有界矩模型中的安全阶数高于探测模型。特别是，信息泄露 压缩和低熵掩码方案利用了特殊类型的编码，使得其泄漏分布的最低密钥相关 统计矩大于份额数量，前提是泄漏函数的确定性部分是线性的[25,41],即，如果 Gj i= Id在公式（2）中。注意，这一要求不应与公式（2）的全局线性要求相混 淆。也就是说，掩码通常为了安全所需的是各个份额以线性方式组合（即公式 （2）是Gj i（Yi（j））的一次多项式）。而信息泄露压缩和低熵掩码方案还额 外要求（局部的）Gj i函数是线性的。

前面的例子表明，理论上存在这样的泄漏函数：在有界矩模型中的安全阶 数高于探测模型中的安全阶数，这足以证明两者之间的分离。然而，如前所述， 在实践中，双轨预充电实现所需的相同（或线性）泄漏假设（分别对应于信息 泄露压缩和低熵掩码方案）极难满足（或尚未得到充分研究）。因此，这种分 离并不适用于所有实现。接下来，我们将介绍一种更具普遍性的分离。

8.2 连续泄露分离

针对算法刷新的连续探测攻击1. 到目前为止，本文的分析主要考虑了“一次性” 攻击与安全性。然而，在实际中，最现实的泄漏模型考虑的是能够持续观察目 标算法多次执行的攻击者。这通常对应于标准的DPA场景，其中通过结合多次 连续运行的观测结果来提取敏感信息[43]。这种场景在伊沙伊、萨哈伊和瓦格 纳提出的连续 t‐探测模型中有所体现[42],，其中攻击者可以学习算法每次执行 过程中计算产生的 t中间值。这意味着随着时间推移，攻击者可能学到的信息 远不止 t这些值

– 特别是多于 d，即份额数量。具体而言，在持续进行 q次执行的攻击中，攻 击者最多可以获取 tq个中间值，这些中间值在算法的各次执行中均匀分布。

设计在连续 t‐探测模型下实现安全性的强掩码刷新方案是一项非平凡的任 务。在本节中，我们证明对于任意份额数量 d，如果连续执行刷新 d次，并且 在每次执行中攻击者最多可以学习到3个中间值，则算法1可能被攻破。为了说 明该攻击方法，我们首先将该算法推广至 d次执行，其中 a(0) 1,…, a(0) d是某个 秘密比特a的初始编码，如[15]中的算法3所示。下面的引理给出了该攻击。在 有界泄漏模型下，类似攻击被用于内积掩码[35]。

算法2. d‐次执行并行刷新算法。

输入： 满足 ⊕i a (0) d随机向量 r(i)。

输出： 满足⊕i a (d)

对于 i= 1 to d 执行 a(i)= a(i−1) ⊕ r(i) ⊕ rot(r(i),1); end for 返回 a(d).

引理2。 设 a为一个均匀选择的秘密比特， d ∈ N为份额数量，并考虑算法2。在for 循环的每一次迭代中，均存在一组3个探针，使得经过 d次迭代后，秘密 a可以被获知。

证明。 我们证明，如果攻击者能够在 d次迭代的并行刷新中，每次迭代探测3 个中间值，则他可以恢复秘密比特 a。该证明采用归纳法，我们证明在了解第 i 次迭代中3个探测点的值后，攻击者便知道a的前 i个份额之和，即 Ai 1: =⊕ i j=1 a (i) j 。由于 Ad 1:=⊕ d j=1 a (d) j = a，经过 d次迭代后，攻击者便知道了 a 的值。在第一次迭代中，仅需对份额 a(1) 1进行一次探测即可获知 A1 1:= a(1) 1 。现在我们证明归纳步骤。令1< ≤ d。假设在第(−1)次执行后，我们知道： A−1 1:=⊕ −1 j=1 a(−1) j 。在第 次迭代中，攻击者探测 r() d , r() −1 和 a() ，从而 能够利用以下等式计算出 A 1： A 1 = ⊕ j =1 a() j = a() ⊕ −1 ⊕ j =1 a() j = a() ⊕ −1 ⊕ j =1 a(−1) j ⊕ r() j ⊕ r() j −1 = a() ⊕ r() d ⊕ r() −1 ⊕ −1 ⊕ j =1 a(−1) j = a() ⊕ r() d ⊕ r() −1 ⊕ A −1 1 ,

其中我们采用约定：对于任意 j，我们有 r(j)) 0 = r(j)) d 。由于在最后一次等式之后 的所有值要么是在前一轮已知的，要么是在当前轮次中获得的，因此上述过程完成 了证明。

算法的连续安全性1在有界矩模型中。 之前的攻击关键依赖于这样一个事实： 攻击者可以在不同迭代之间自适应地移动其探测点，即在第 i次执行中，他必 须学习到与第(i −1)次执行不同的值。这意味着在实际中，他需要联合利用来 自功耗轨迹的 ≈ 3d个不同的时间样本。我们现在证明，在（连续）有界矩模 型中，此类攻击是不可能实现的。连续有界矩模型与单次有界矩模型的唯一区 别在于，前者提供了更多组合泄漏的方式，因为其周期数是前者的 q倍。更准 确地说，将有界矩安全性自然地扩展到连续场景时，要求攻击者所观察到的 q 个泄露向量中的任意 o次多项式的泄露样本的期望，独立于实现的 q次执行过 程中产生的任何敏感变量 Y ∈{0, 1}。根据引理1，我们知道该条件成立的一 个充分条件是所有单项式的期望均独立于 Y。因此具体而言，我们只需要对任 意一组可能的时钟周期 o、 c1、 c2…、 co ∈[1, qN]，满足： Pr[Y= 0]= Pr[Y= 0|E[Lc1 × Lc2 ×… × Lco]], Pr[Y= 1]= Pr[Y= 1|E[Lc1 × Lc2 ×… × Lco]].

在单次有界矩模型 c1, c2…, co中，仅在 [1, N] 中运行。我们接下来的分离 结果还需要针对无状态原语进行专门化。所谓无状态，是指诸如分组密码之类 的原语，它们只需要在每次执行之间在内存中维护一个恒定的密钥。

定理4。 在连续有界矩模型中，若一个无状态原语的实现使用算法1刷新密钥， 并且其在单次探测模型中在阶 o上是安全的，则该实现也在阶 o上是安全的。

证明（概要）。 我们考虑一个算法，其单次执行需要N个时钟周期，并重复执 行 q次。我们可以将该算法的 q次执行视为一个持续运行 qN个时钟周期的计 算过程。由于我们仅关注保护无状态原语，各次执行之间仅通过其刷新后的密 钥相互关联。因此，该 q次对 N个周期的掩码实现的执行可被视为一个电路， 其中包含使用算法1进行的 q次密钥刷新，每次刷新后的密钥作为无状态掩码 实现的输入。如果我们能够证明这个“扩展”后的电路在总共 qN个时钟周期 内可抵御至多 o个探测点的攻击者（总探测次数而非连续探测模型中的每次执 行单独计算），则根据定理1即可得出结论。

为此，我们首先注意到，在属于 q次刷新的部分中设置 o个探测点并不会使攻击者 能够获取掩码的密钥。这源于以下事实：在刷新操作的单次执行（算法 o）中探测1）不会允许攻击 者学习到该掩码的密钥。更准确地说，刷新过程中的任何此类探测均可直接转 换为对初始编码的探测（并将刷新所使用的随机性免费提供给攻击者）。这意 味着，在刷新部分的任何探测最多只能获得进入无状态掩码实现的掩码密钥的 一个份额。此外，根据假设，我们知道该实现的单次执行是 o‐探测安全的。这 意味着即使在掩码实现内部进行了 o次探测后，仍必须存在一个掩码状态的份 额，这些探测与其无关。更一般地，在掩码实现中放置 o−i个探测意味着这些 探测至少与 i+ 1个掩码状态的份额无关，否则剩余的 i个探测可被放置在未 知的输入共享上，从而与掩码的密钥产生关联。因此，我们可以揭示输入编码 的所有份额，仅保留这 i+ 1个独立的份额。于是，通过简单地累加探测数量， 我们得出结论：即使在扩展电路内部放置 o个探测，仍然能够保持安全性。

需要注意的是，当考虑有状态原语时，上述关于扩展电路和特殊刷新方式 的论证将不再成立。在这种情况下，刷新操作可能与电路的其他部分发生交互。因此，为了在这种情况下实现安全性，我们需要更强（可组合）的刷新机制， 以应对算法1可能出现在计算中任意位置的情况。如前所述，有界矩模型中的 安全性要求明显弱于探测模型，而这正是使我们能够取得这一积极结果的原因。直观上讲，探测模型中的安全性要求是在给定一定数量探测点的情况下不发生 任何信息泄露；相比之下，有界矩模型中的安全性仅要求该信息难以被利用， 这一点体现在攻击者所观察到的泄漏分布中最低的信息性统计矩是有界的。该 模型很好地反映了实际侧信道攻击的情形：攻击者可以获得泄漏轨迹中的所有 采样点（如图1所示），而我们希望确保他至少必须估计该泄漏分布的高阶矩才 能提取出敏感信息（如果分布具有足够噪声，则该任务在 o上是指数级困难的）。

我们认为这一最终结果对密码工程师尤其重要，因为它澄清了掩码方案理论与 实践中长期存在的一个差距，即是否需要复杂的刷新方案。具体而言，我们能 够证明第6.1节中所述的简单刷新方案确实足以抵御实际的高阶侧信道攻击。

同样值得注意的是，研究我们的简单刷新方案在连续噪声泄漏模型中的安 全性是一个有趣的开放性问题。直观上，将引理2的攻击扩展到此场景似乎很 困难。以第二步为例：我们已经学习了 A1 1 ，并希望利用三个噪声探测点来学 习 A2 1 。如果噪声导致我们无法精确地学习到 A2 1 ，那么再次观察具有独立噪 声的三个探测点并不会带来太大帮助（因为我们

无法轻易地将关于新 A21的信息结合起来，并且需要收集所有 d份额的信息，以 累积关于固定秘密的信息）。至于第5节中的定理1，我们仍然可以注意到，有 界矩模型相较于（更通用但更复杂的）噪声泄漏模型，能够更容易地与（更理 论化的）探测模型建立联系。

9 独立性问题

在结束之前，我们讨论阈值实在硬件（并行）实现中的一个关键优势，即其对 毛刺具有更强的抵抗力。我们将利用并推广这一讨论，以阐明可能影响泄漏实 现的各种独立性问题，并详细说明如何解决这些问题，从而获得实际实现，以 达到掩码安全证明所保证的安全级别。

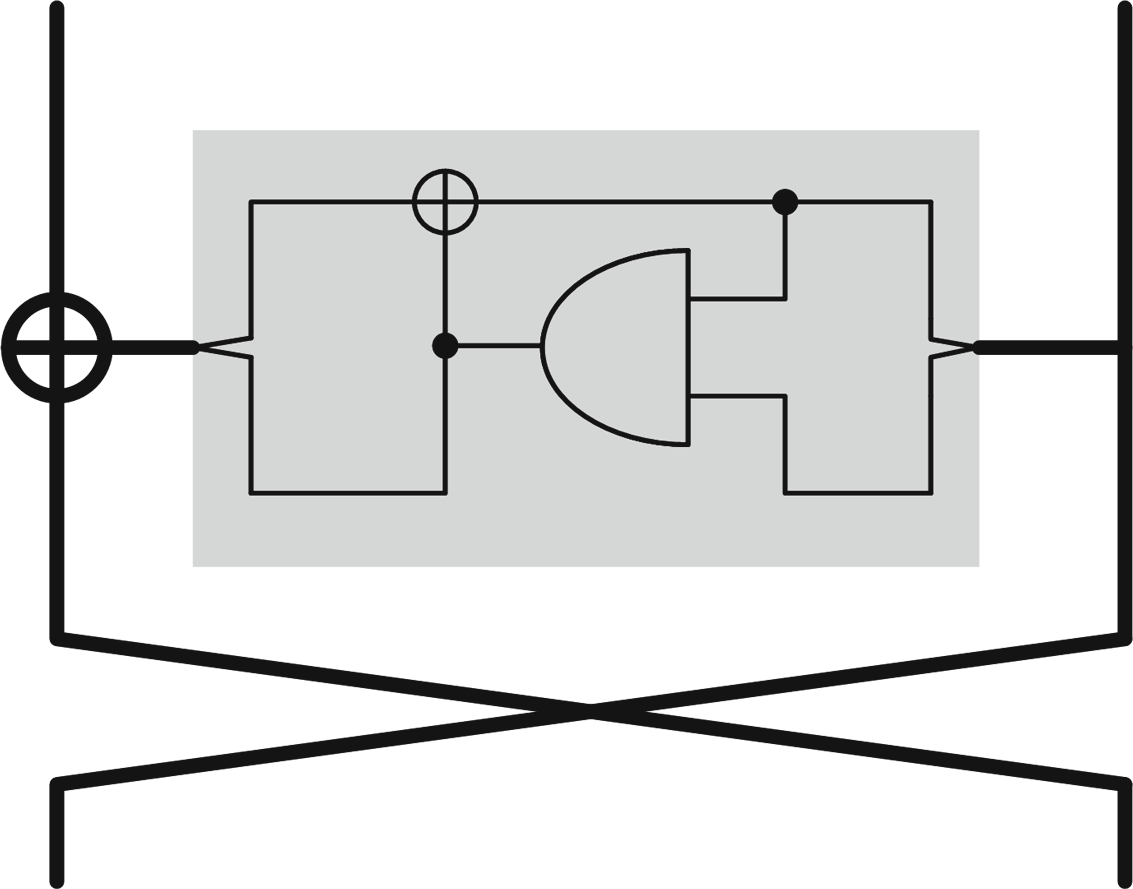
实现默认设置。 作为起点，我们在图6(a)中复现了一个阈值实现的标准示例， 该示例对应于一个小布尔函数 f(x)的安全执行，其中该函数以及输入/输出均被 分为三份进行共享。在该图中，（浅色和深色）灰色矩形代表寄存器，蓝色圆 圈代表组合电路。从该示例中，我们可以列出实际中可能发生的三种不同类型 的独立性问题：

1. 计算重组合（或毛刺）。 在第一种情况下，瞬态中间计算导致电路的组合部 分重新组合了份额。这种效应在文献中常被称为“毛刺”，并已被利用来破坏 （即降低安全阶数）许多硬件实现的安全性（例如 [46]）。
2. 存储重组合（或转换）。 在这种第二种情况下，非独立性来源于寄存器复用， 以及实际泄漏可能与寄存器状态之间的转换成正比。例如，如果图6（a）中的 寄存器 x1和 y1（其依赖于 x2、 x3）是同一个，则会发生这种情况。这种现象 在文献中也经常被观察到，被称为“基于距离”或“基于转换”的泄漏，并已 被用于攻破软件实现（例如，[11,29]）。
3. 布线重组合（或耦合）。 在最后一种情况下，重组合基于线路的物理邻近性。泄漏函数将与这些线路的某个函数成正比。这类效应被称为“耦合”，在存在 复杂（例如二次）函数的情况下，可能破坏式（2）中的加性模型。据我们所知， 目前尚未在具体的（已发表的）攻击中被利用。

毛刺、阈值实现与非完备性。 阈值实现的一个重要贡献是引入了一种可靠的算 法方式来处理毛刺问题。为此，它们要求其实现满足“非完备性”属性，该属 性要求（在阶数 o下）任意最多 o个组件函数 fi的组合必须至少独立于一个 输入共享[21]。有趣的是，如图6(b)所示，我们的并行乘法算法天然满足这一 属性，这与之前的观察结果一致[55]，也符合基于二次函数分解来综合构造阈 值实现的标准方法[23]。需要注意的是，阈值实现的关键在于通过寄存器隔离 非完备的 fi函数。因此，为了在 [15],中高效且无毛刺地实现算法3，通常建议 在更大的域中实现它（例如通过将我们的乘法算法扩展到GF(28) 中，如同 AES那样），或通过位切片利用并行性[40]。

基于转换的泄露。 针对此目的存在多种设计方案。最直接的方法是确保实现中 的所有寄存器均不相同，或加倍掩码方案 [11] 的阶数。但这显然不是最优的 （因为并非所有转换都会泄露敏感信息）。因此，更好的解决方案是在评估掩 码实现时纳入基于转换的泄露，这一任务也可受益于 [13] 中的工具。

耦合。 这种最后的效应本质上是物理性的，因此没有算法/软件方法可以防止它。在并行实现的背景下，耦合尤其关键，因为它们所隐含的非线性可能会破坏独 立泄露假设。（相比之下，在串行实现中，通过在不同时刻操作份额，该假设 更容易得到满足）

时钟周期）。因此，在并行掩码实现中不发生基于路由的重组，这基本上是所 有设计者都必须做出的一个假设。在这方面，我们注意到针对阈值实现的攻击 实验结果表明，当多个份额被并行处理时（例如第4.1节列出的那些），这一假 设对于当前技术确实得到了很好的遵守。然而，我们也注意到，随着技术缩放， 耦合的风险会增加[51]。因此，在后一种情况下，无论如何，一个好的设计策 略是在更大的域中操作份额，或者如果以位切片方式实现掩码，则确保它们之 间有足够的物理距离。

10个开放问题

这些结果为进一步研究指明了两个重要方向。

首先，我们引入的有界矩模型可以被视为概念上简单的探测模型和实际相 关的噪声泄漏模型之间的中间路径。正如第8节（以及图7）所讨论的，有界矩 泄漏模型严格弱于探测模型。因此，研究有界矩安全性是否对某些类别的泄漏 函数意味着噪声泄漏安全性将十分有意义。显然，这在一般情况下不成立，因 为存在具有相同矩的不同分布。然而，鉴于基于矩的安全评估所带来的效率优 势，确定该方法在哪些情境下是充分的——即找出泄漏分布在何时能被其矩足 够好地表示——是一个有趣的开放问题。为此目的，基于并形式化[34]中的结果 是一个有趣的研究方向。

其次，每当在掩码实现中发现偏差时，我们的工具不仅输出导致该偏差的 计算，还会输出其（可能很小的）幅度。因此，有界矩模型具有将[39]中的定 量分析（迄今为止仅限于一阶泄漏）扩展到高阶情况的巨大潜力。依赖于这些 偏差在数量上难以利用这一事实，可能会进一步减少掩码实现中的随机性要求， 例如通过将这些偏差的评估与[32]（第4.2节）中引入的分析非独立泄漏的工具 相结合。