慎用C++关键字auto：Eigen库中的类型推断陷阱

最新推荐文章于 2025-12-21 21:47:42 发布

原创最新推荐文章于 2025-12-21 21:47:42 发布 · 414 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #开发语言

该文章已生成可运行项目，

在C++编程中，auto关键字虽然提供了便利的类型推断功能，但在使用Eigen库进行线性代数运算时，过度依赖auto可能导致严重的运行时错误和性能问题。比如我们在计算传感器之间的变换矩阵时，分别已知传感器AB到C的变换矩阵，那么计算A到B的变换矩阵时，不可避免的需要求逆计算。本文将详细分析这一问题，并提供相应的解决方案。

1. 问题复现

首先我们定义4个外参矩阵：

std::vector<Eigen::Matrix4d> getTransformations() {
  std::vector<Eigen::Matrix4d> mats(4);
  mats[0] << 0.999981, -0.00415212, -0.00466134, 0.71,  //
      0.00414895, 0.999991, -0.000689198, 0,            //
      0.00466416, 0.000669844, 0.999989, 1.85264,       //
      0, 0, 0, 1;

  mats[1] << -0.999819, -0.0184469, -0.00462907, 0.800784,  //
      -0.00444588, -0.00995929, 0.999941, 0.601399,         //
      -0.0184919, 0.99978, 0.00987548, 1.63478,             //
      0, 0, 0, 1;

  mats[2] << 0.00987783, 0.00454281, -0.999941, -0.910941,  //
      -0.999715, -0.0216873, -0.00997413, -0.002741,        //
      -0.0217313, 0.999754, 0.00432729,
      1.19948,  //
      0, 0, 0, 1;

  mats[3] << 0.999939, 0.00712378, 0.00849454, 0.811098,  //
      0.00856168, -0.00944788, -0.999919, -0.620238,      //
      -0.00704294, 0.99993, -0.00950829,
      1.67974,  //
      0, 0, 0, 1;

  return mats;
}

然后我们计算所有矩阵相对于首帧的变换矩 $Ti=T0−1⋅TiT_{i} = T^{-1}_{0} \cdot T_{i}$ ：

const auto raw_mats = getTransformations();
std::vector<Eigen::Matrix4d> T_sensors2base = raw_mats;
// 注意这里，我们用了auto来承载第一个矩阵的逆矩阵
const auto T_trans = T_sensors2base[0].inverse();
const int num = T_sensors2base.size();
for (int i = 0; i < num; i++) {
  auto &T = T_sensors2base[i];
  LOG(INFO) << "idx: " << i << ", src mat: \n"
            << T << "\ninv mat: \n"
            << T_trans;
  T = T_trans * T;
  LOG(INFO) << "idx: " << i << ", dst mat: \n" << T;
}

观看实际结果，第一个矩阵变成单位阵没问题，但从第二个矩阵开始，变换矩阵莫名奇妙变成单位阵了！！！
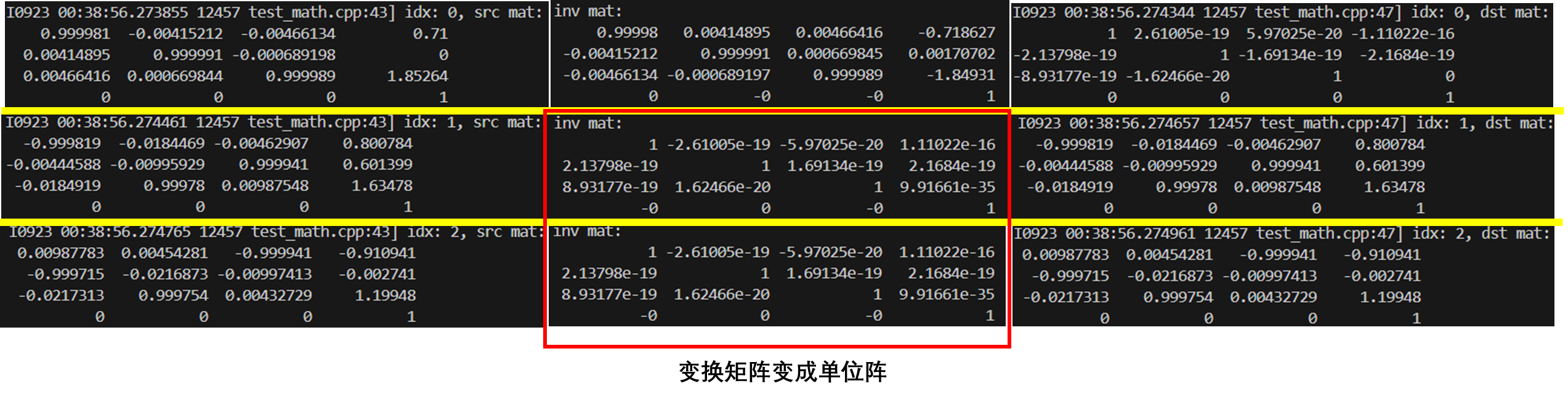
在这里插入图片描述

2. 原因分析

Eigen库采用表达式模板技术来优化矩阵运算，这种设计会导致auto推断出临时表达式类型而非最终结果类型。我们可以发现inverse()的返回值是Eigen::Inverse<Eigen::Matrix4d>而非我们以为的Eigen::Matrix4d类型。这个表示的是"将来需要计算A的逆"的表达式模板对象。

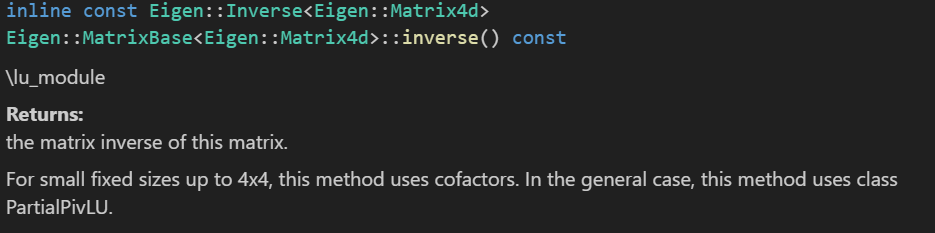
在这里插入图片描述
基于这个逻辑，那么：

计算第一个矩阵时，实际是T_sensors2base[0] = T_sensors2base[0].inverse() * T_sensors2base[0]，T_sensors2base[0]变为单位阵。
但计算第二个矩阵时，实际是T_sensors2base[1] = T_sensors2base[0].inverse() * T_sensors2base[1]，T_sensors2base[0]已经是单位阵了，因此没有得到我们预想的结果。

3. 解决方案

知道了问题，那么解决方案就非常简单咯，显示定义Eigen::Matrix4d来存放这个逆矩阵即可。这种方法通过强制类型转换和立即求值，确保了逆矩阵被正确计算并存储在确定类型的变量中。

// const auto T_trans = T_sensors2base[0].inverse();
const Eigen::Matrix4d T_trans = T_sensors2base[0].inverse();

在这里插入图片描述

4. 小结

本文介绍的auto问题，不会在编译时被捕获。更危险的是，表达式模板的生命周期结束时，使用auto声明的变量可能持有悬空引用，导致难以调试的运行时错误。

当然，慎用auto不代表不能用，有几个技巧可以在实际开发时注意下：

显式指定类型。对于矩阵/向量变量，始终使用具体类型如Eigen::MatrixXd、Eigen::Vector3f等来表示。
强制立即求值‌。如果待处理的公式包含大量矩阵变换，我们可以先用auto把这个复杂表达式构造出来，然后使用.eval()方法强制求值并转换为具体类型。
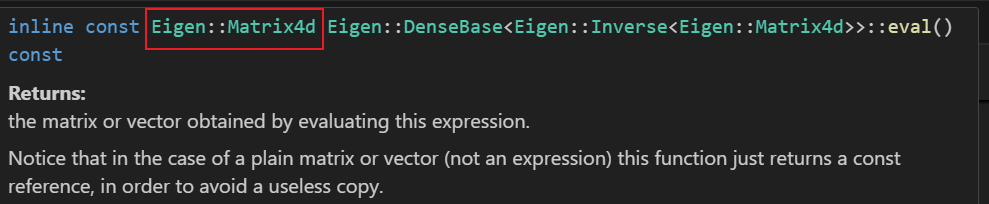
调用函数时确认下返回值。鼠标悬停函数上即可看到函数定义细节（如果没有快去安装vscode插件→_→）