Shader开发（三）向量入门-优快云博客

本文链接：https://blog.youkuaiyun.com/ZeroBugX/article/details/149635489

引言

在计算机图形学中，向量（Vector）是一个核心概念。无论是定义物体的位置、描述运动方向，还是进行光照计算，向量都扮演着不可或缺的角色。很多人初次接触向量时，会听到“向量是一个既有方向又有大小的量”这样的定义。虽然准确，但不够直观。本文将通过通俗的比喻和示例，带你深入理解向量的基本概念及其在3D图形中的应用。

向量的基本概念

1. 向量的定义

向量本质上是一个方向和一个大小（或长度）的组合。为了更容易理解，可以把向量想象成自驾游中的一段路程。比如，你要“向北行驶3英里”，这个“向北3公里”就是一个向量：方向是“北”，大小是“3公里”。

在图形学中，向量通常用箭头表示。箭头的方向代表向量的方向，长度则代表大小。需要注意的是，向量本身不包含具体的位置信息，它只是描述一种“位移”或“运动”。因此，同一个向量可以在空间的不同位置出现，如图1-3所示。

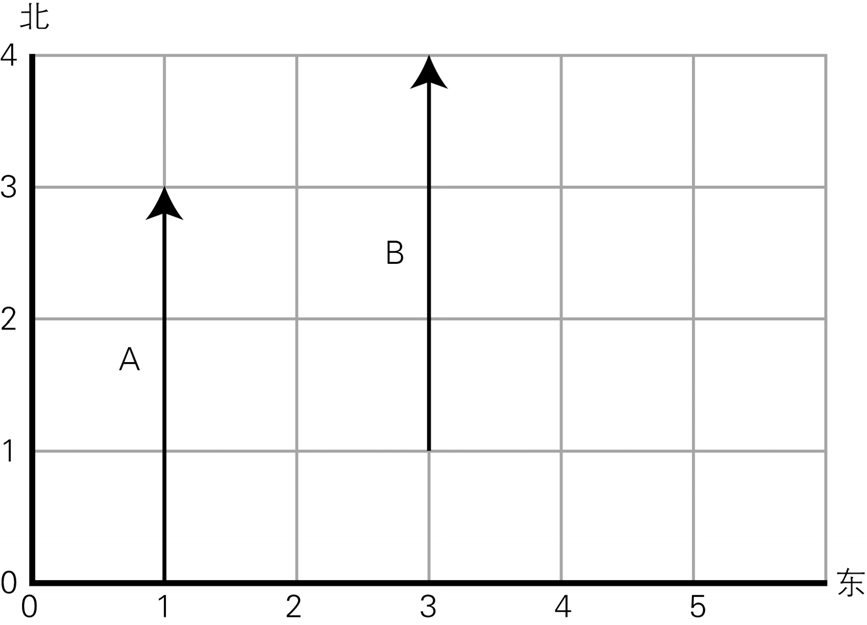
图1-3 两个位置上的相同向量

在图1-3中，箭头A和B起点不同，但方向和长度相同，因此它们是同一个向量。

2. 向量与位置

虽然向量不直接表示位置，但在图形学中，我们常用向量来描述物体在空间中的位置。这时，向量的起点通常假定为坐标系的原点，例如2D中的(0,0)或3D中的(0,0,0)。比如，位置(2,1)可以理解为从原点出发，沿X轴移动2个单位，沿Y轴移动1个单位，如图1-4和图1-5所示。

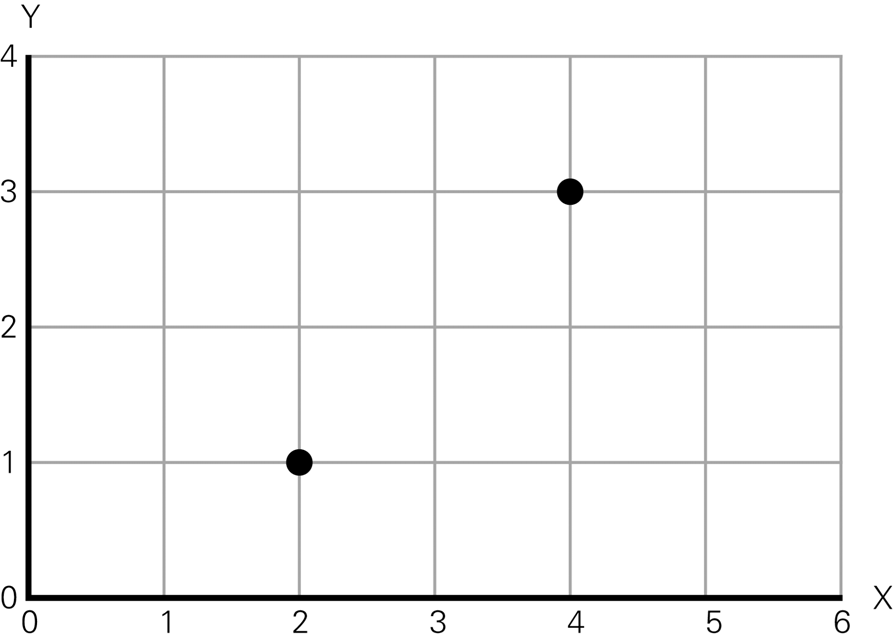
图1-4 空间中的两个位置

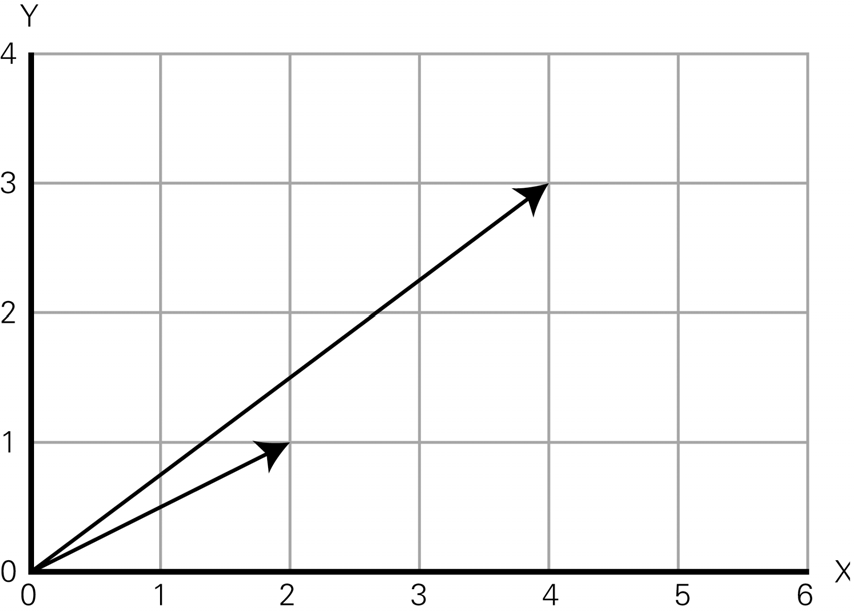
图1-5 将向量线添加到图1-4中的位置

在图1-5中，箭头从原点指向位置点，清晰地展示了位置向量的概念。

3. 向量的分量

向量通常用一组数字表示，例如(1,2,3)，这些数字称为向量的分量。分量的数量决定了向量的维度：

2D向量：(x, y)
3D向量：(x, y, z)
4D向量：(x, y, z, w)

在图形学中，4D向量常用于齐次坐标，其中w分量在透视除法等操作中起到关键作用。在着色器代码中，常见的变量类型如vec2、vec3、vec4分别表示2、3、4分量的向量。

向量的加减法

1. 向量的加法

向量的加法就像自驾游中多个路段的累积。比如，你先向东行驶2英里，再向北行驶3英里，最终的位移可以用一个向量表示，这个向量从起点直接指向终点，如图1-6所示。

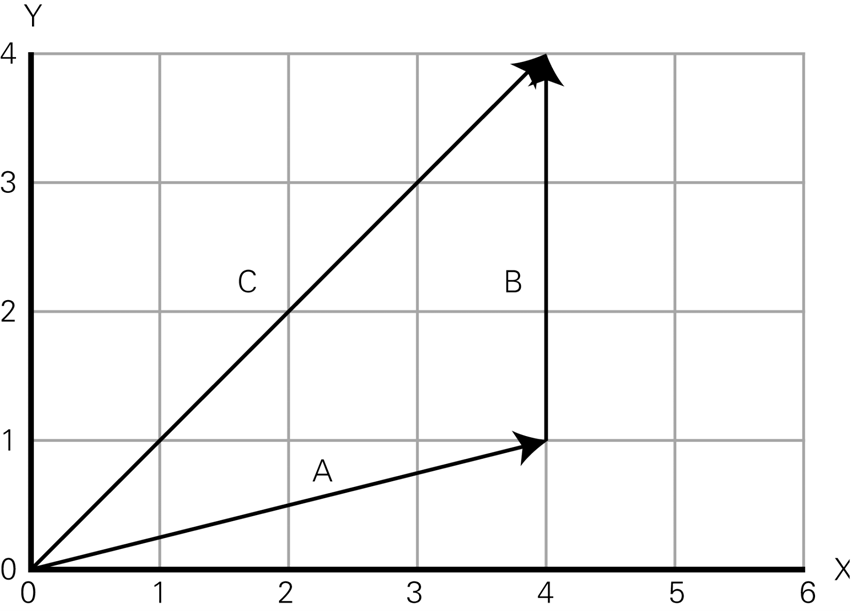
图1-6 向量A 和B 相加，结果是向量C

数学上，向量加法是分量相加： $[(a_x, a_y) + (b_x, b_y) = (a_x + b_x, a_y + b_y)]$

例如： [(200, 200) + (200, 100) = (400, 300)]

2. 向量的减法

向量的减法类似于求两个位置之间的相对位移。比如，从位置(400,300)减去(200,200)，结果是(200,100)，表示从(200,200)到(400,300)的位移向量。

数学表示： $[(a_x, a_y) - (b_x, b_y) = (a_x - b_x, a_y - b_y)]$

向量的标量乘除

1. 标量乘法

将向量乘以一个标量（普通数字），相当于缩放向量的长度，同时保持方向不变（如果标量为负数，则方向反转）。比如，一个“向北3英里”的向量乘以5，结果是“向北15英里”。

数学表示： $[k \times (x, y, z) = (k \times x, k \times y, k \times z)]$

例如： $[5 \times (1, 3) = (5, 15)]$

2. 标量除法

标量除法是标量乘法的逆运算，将向量的每个分量除以标量。

例如： (10, 20) / 2 = (5, 10)

向量的归一化

1. 单位向量

单位向量是长度为1的向量。它在表示方向时非常有用，因为通过将单位向量乘以任意标量，可以得到该方向上任意长度的向量，如图1-7所示。

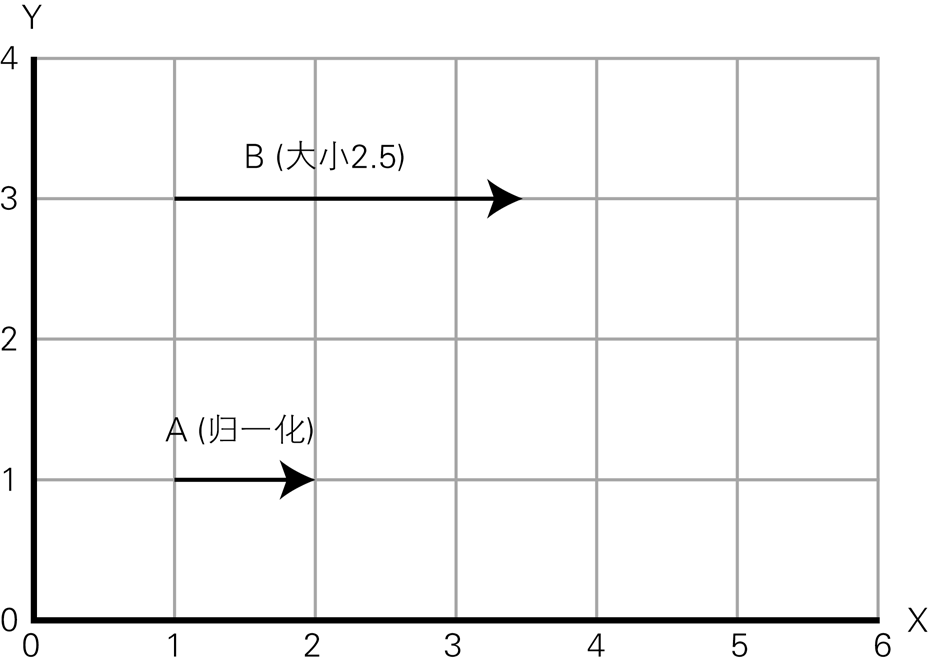
图1-7 单位向量及其缩放

在图1-7中，向量A是单位向量，向量B是A乘以2.5，长度正好是2.5。

2. 归一化

将一个非单位向量转换为单位向量的过程叫归一化。归一化通过将向量的每个分量除以向量的长度（或称模）来实现。

例如，向量(3,4)的长度是5（因为 $( \sqrt{3^2 + 4^2} = 5 )$ ），归一化后为(0.6, 0.8)。

在着色器中，通常使用内置函数（如normalize）来归一化向量，无需手动计算。

向量的分量乘除

在图形编程中，有时需要对向量的分量逐个相乘或相除，这在处理颜色、纹理坐标等数据时非常实用。

1. 分量相乘

两个向量的分量相乘： $[(a_x, a_y, a_z) \times (b_x, b_y, b_z) = (a_x \times b_x, a_y \times b_y, a_z \times b_z)]$

例如： $[(1,2,3) \times (4,5,6) = (4,10,18)]$

2. 分量相除

类似地： $[(a_x, a_y, a_z) / (b_x, b_y, b_z) = (a_x / b_x, a_y / b_y, a_z / b_z)]$

例如： $[(1,2,3) / (4,5,6) = (0.25, 0.4, 0.5)]$

这种分量运算在传统向量数学中不常见，但在图形学中非常实用，尤其在颜色混合、纹理采样等场景中。

图形编程中的特殊向量运算

在深入到着色器代码之前，需要了解最后一点向量数学知识：如何用另一个向量乘或除一个向量。就像乘以标量值一样，这些操作也是按分量进行的：

(1,2,3) × (4,5,6) = (1×4, 2×5, 3×6) = (4,10,18)
(1,2,3) ÷ (4,5,6) = (1÷4, 2÷5, 3÷6) = (0.25,0.4,0.5)

为什么会有这些运算？

如果你学习过计算机图形学以外的向量，这两个例子可能会让你感到困惑，因为它们并不是标准向量数学的一部分。

这样做的原因是，虽然向量在数学和物理中有一个非常正式的定义，但在代码中，向量只是一个有序的数字序列，有时前面的运算对某些类型的数据来说是有意义的或只是很方便。

颜色向量的应用

一个典型例子是当向量存储颜色而不是位置和方向时。以这种方式将一种颜色与另一种颜色相乘是非常有用的：

// 颜色混合示例
vec3 baseColor = vec3(1.0, 0.5, 0.2);  // 橙色
vec3 tint = vec3(0.8, 1.0, 0.6);       // 绿色调
vec3 result = baseColor * tint;         // 混合结果

向量与颜色存储

正如刚才提到的，向量不仅用于存储位置和方向信息，还广泛用于存储颜色数据。取决于你以前编写的程序的类型，向量如何存储颜色数据可能并不是众人皆知，这是图形代码中一个重要的应用领域。

在图形编程中，颜色通常用3分量向量（RGB）或4分量向量（RGBA）来表示：

vec3 redColor = vec3(1.0, 0.0, 0.0);        // 纯红色
vec4 blueWithAlpha = vec4(0.0, 0.0, 1.0, 0.5); // 半透明蓝色