凸集（Convex sets）_relative interior数学-优快云博客

本文介绍了凸集和仿射集的基本概念，包括直线、线段、仿射维度及相对内部等，同时还探讨了超平面、半空间、欧几里得球和椭球等重要凸集的例子。

凸集（Convex sets）

1 仿射集（affine sets）和凸集（convex sets）
2、一些重要的（凸集）例子
- 2.1 超平面（Hyperplanes）和半空间（halfspaces）
- 2.2 欧几里得球（Euclidean balls）和椭球（ellipsoids）

1 仿射集（affine sets）和凸集（convex sets）

1.1 直线（lines）和线段（line segments）

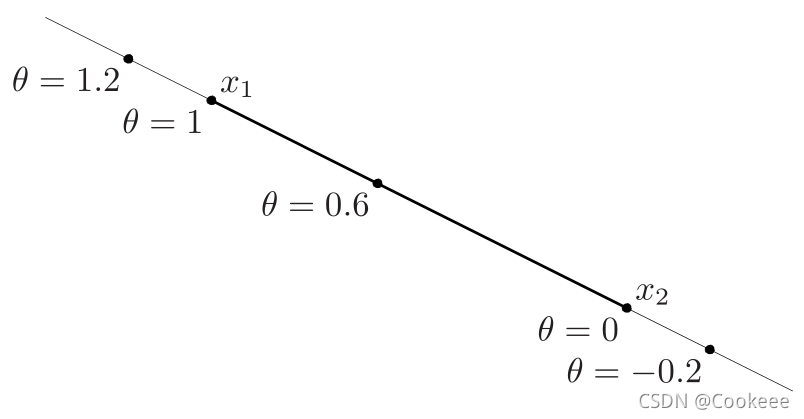
假如 $x_1\neq x_2$ 是 ${\bf R}^n$ 上的两点，点 $y=\theta x_1 +\left( 1-\theta\right)x_2$ （其中 $\theta \in \bf R$ ），组成了穿过 $x_1$ 和 $x_2$ 的直线。 $0$ 到 $1$ 之间的 $\theta$ 值对应的点 $y$ 组成了 $x_1$ 和 $x_2$ 之间的线段。
$y$ 的另一种表达形式为： $y=x_2+\theta \left( x_1-x_2\right)$ 很容易理解， $x_2$ 是基准点， $\theta \left( x_1-x_2\right)$ 是在 $\left( x_1-x_2\right)$ 方向上的延申，通过二维空间进行理解。

1.2 仿射集

一个集合 $C\in {\bf R}^n$ ，如果经过 $C$ 中任意两点的直线还是位于 $C$ 内，即对于任意的 $x_1,x_2 \in C$ 和任意 $\theta \in \bf R$ ，有 $\theta x_1 +\left( 1-\theta\right)x_2 \in C$ ，那么这个集合 $C$ 就是仿射的。换句话说就是， $C$ 包括了 $C$ 中任意两点的 系数和为 $1$ 的 线性组合。
指定点 ${\theta}_1 x_1+...+{\theta}_k x_k$ ，其中 ${\theta}_1+...+{\theta}_k=1$ ，为点 $x_1,...,x_k$ 的仿射组合。仿射集的定义就是包括其中任意两点的仿射组合的集合，推广到“仿射集包括其中任意多点的每一个仿射组合”，简单证明如下：

可用归纳法严格证明。

线性方程组的解集 $C=\lbrace x \vert Ax=b\rbrace$ 是一个仿射集，证明略。
事实上，每个仿射集都可以表示为线性方程组的解集。

某个集合 $C\subseteq{\bf R}^n$ 里的点的所有仿射组合的集合被称为 $C$ 的仿射包（affine hull），表示为 $\text {\bf aff}\enspace C$ ：
$\text {\bf aff}\enspace C=\lbrace {\theta}_1x_1+\cdots+{\theta}_kx_k \: \vert \:x_1, \ldots, x_k \in C,{\theta}_1+ \cdots + {\theta}_k=1 \rbrace.$ 仿射包是包含 $C$ 的最小的仿射集，即如果 $S$ 是任意一个仿射集并且 $C\subseteq S$ ，有 $\text {\bf aff}\enspace C \subseteq S$ 。

1.3 仿射维度（affine dimension）和相对内部（relative interior）

定义一个集合 $C$ 的仿射维度为它的仿射包的维度。仿射维度与其他关于维度的定义不一样，比如， ${\bf R}^2$ 上的单位圆的仿射包是整个 ${\bf R}^2$ ，所以它的仿射维度为 $2$ ，但是大多数对维度的定义都认为 ${\bf R}^2$ 上的单位圆是一维的。
定义一个集合 $C$ 的相对内部为 $\text{\bf relint} \: C$ ，其中 $\text{\bf relint} \: C \subseteq C \subseteq \text{\bf aff} \: C$ ，并且 $\text{\bf relint} \: C = \lbrace x\in C \: \vert \: B\left( x,r\right) \cap \text{\bf aff} \: C \subseteq C, r>0 \rbrace,$ 其中 $B\left( x,r\right)=\lbrace y \: \vert \: \lVert y -x \rVert \leq r\rbrace$ 是圆心为 $x$ ，半径为 $r$ 的范数球。
定义集合 $C$ 的相对边界为 $\ relint C = { x ∣ x ∈ cl C and x ∉ relint C } \text {\bf cl} \: C \: \backslash \: \text {\bf relint} \: C=\lbrace x \: \vert \: x\in \text {\bf cl} \: C \: \text {and} \: x \notin \text{\bf relint} \: C\rbrace$ ，其中 $\text {\bf cl} \: C$ 为 $C$ 的闭包。

1.4 凸集

如果集合 $C$ 中任意两点之间的线段都位于 $C$ 内，即对于任意的 $x_1,x_2\in C$ 和任意 $\theta \left( 0 \leq \theta \leq 1\right)$ ，有 $\theta x_1+\left(1-\theta \right)x_2 \in C$ 则称 $C$ 是凸的。
粗略地讲，如果集合中的任意一点都能被其他所有点沿着一条无障碍的直线路径看到，那么这个集合就是凸的，无障碍意味着路径上的每一点都位于该集合内。

相关定理¹：
若干个凸集的交集还是凸集；
若干个凸集的线性组合还是凸集；
每个仿射集都是凸的，因为它包含任意两个点之间的整条直线，因此也包含线段。

把形式为 ${\theta}_1 x_1+...+{\theta}_k x_k$ ，其中 ${\theta}_1+...+{\theta}_k=1 \: \text{and} \:{\theta}_i \geq0,i=1,\dots,k$ 的点叫做点 $x_1,...,x_k$ 的一个凸组合。

与仿射集一样，可以证明一个集合是凸的，当且仅当它包含它的任意点的每一个凸组合。
几个点的凸组合可以理解为它们的加权平均值， ${\theta}_i$ 为 $x_i$ 在凸组合中的占比。
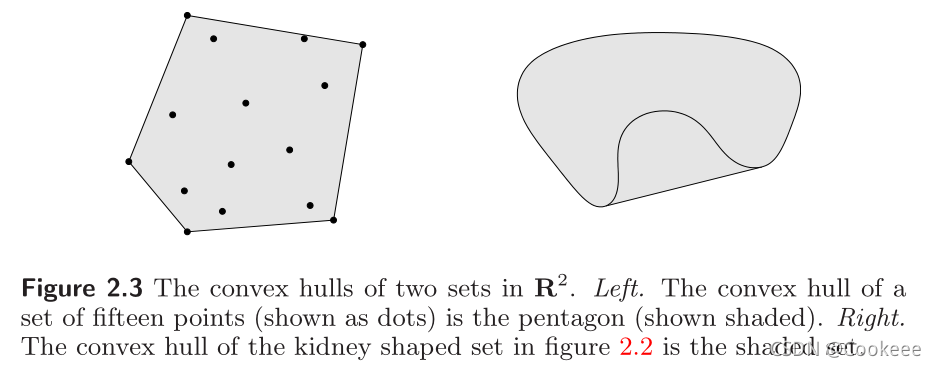
集合 $C$ 的凸包（convex hull）是包含 $C$ 中的点的所有凸组合的集合，表示为 $\text{\bf conv} \: C$ ：
$\text{\bf conv} \: C=\lbrace{\theta}_1 x_1+...+{\theta}_k x_k \: \vert \: x_i \in C,\:{\theta}_i \geq 0,\: i=1,\dots,k,\: {\theta}_1+...+{\theta}_k=1\rbrace$
顾名思义，凸包 $\text{\bf conv} \: C$ 总是凸的，它是包括 $C$ 的最小凸集，即如果 $B$ 是包括 $C$ 的任意一个凸集，则 $\text{\bf conv} \: C \subseteq B$ 。

凸组合的概念可以推广到包括无穷和、积分，以及最一般形式的概率分布。在这里插入图片描述

1.5 锥（Cones）

如果对每个 $\in C$ 和 $\theta \geq0$ ，有 $\theta x \in C$ ，则称集合 $C$ 是一个锥或者是非负齐次性（nonnegative homogeneous）的。
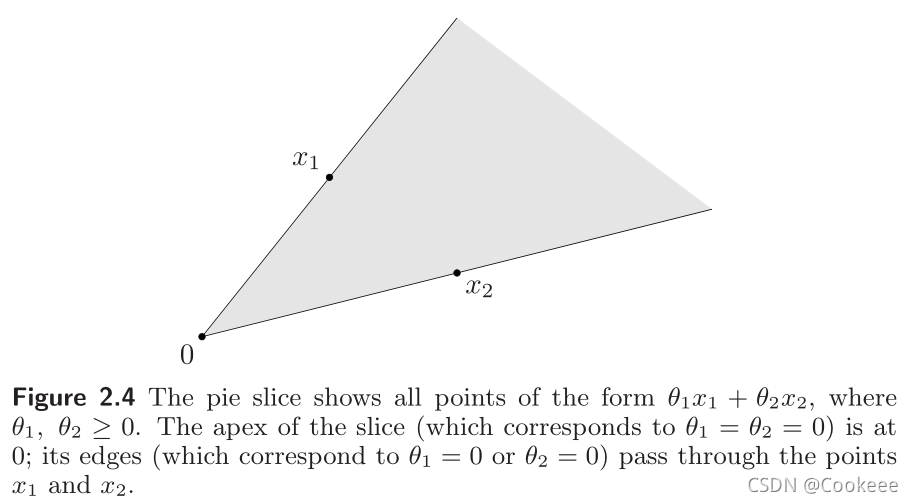
如果集合 $C$ 既是凸的，又是一个锥，则称 $C$ 是一个凸锥（convex cone），即对于任意 $x_1,x_2 \in C$ 和 ${\theta}_1,{\theta}_2 \geq0$ ，有 ${\theta}_1x_1+{\theta}_2x_2 \in C.$ 在这里插入图片描述
一个形如 ${\theta}_1x_1+\cdots+{\theta}_kx_k$ （ ${\theta}_1,\ldots,{\theta}_k \geq0$ ）的点叫做点 $x_1,\ldots,x_k$ 的锥组合（或非负线性组合）。
凸锥 $C$ 里面的点的每一个锥组合都在 $C$ 里面。一个集合是凸锥，当且仅当它包含它的元素的所有锥组合。
像凸组合一样，锥组合的想法可以推广到无穷和和积分。
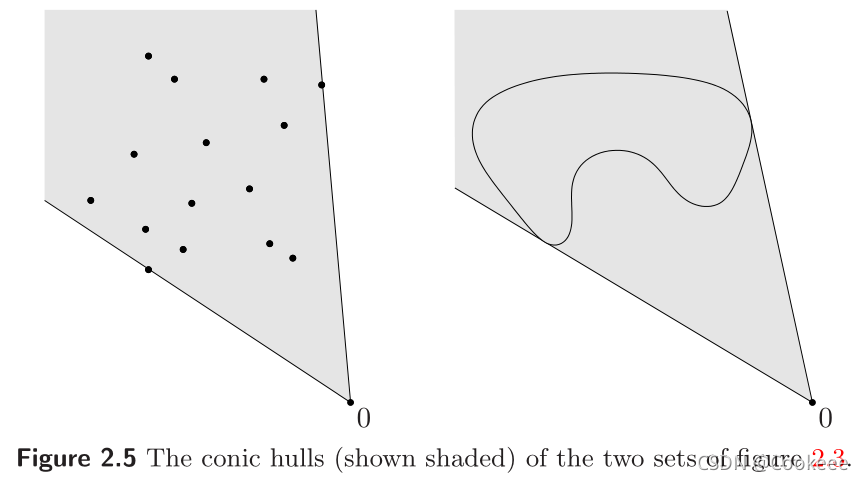
集合 $C$ 的锥包是 $C$ 中点的所有锥组合的集合，即 $\lbrace {\theta}_1x_1+\cdots+{\theta}_kx_k \: \vert \: x_i \in C,\: {\theta}_i \geq 0,\:i=1,\ldots,k\rbrace,$ 也是包括 $C$ 的最小凸锥。
在这里插入图片描述

2、一些重要的（凸集）例子

空集 $\phi$ 、任意单点集 $\lbrace x_0 \rbrace$ 和整个空间 ${\bf R}^n$ 都是 ${\bf R}^n$ 的仿射（因此是凸的）子集。
任意直线（line）是仿射的。一条穿过零点的直线是一个子空间，因此也是一个凸锥。
一条线段是凸的，但不是仿射的（但特殊的线段：一个点，是仿射的）。
一条射线，形式为 $\lbrace x_0 +\theta v\: \vert \: \theta \geq 0 \rbrace,\:v\neq0$ ，是凸的，但不是仿射的。
任何子空间（subspace）都是仿射的，也是凸锥（因此也是凸的）。

2.1 超平面（Hyperplanes）和半空间（halfspaces）

一个超平面是一个形式为 $\lbrace x\:\vert\: a^Tx=b\rbrace$ 的集合，其中 $a\in{\bf R}^n,a\neq 0,b\in \bf R$ 。可以理解为法向量为 $a$ 的超平面，即
$\lbrace x\:\vert\: a^T\left( x-x_0\right)=0\rbrace,$ 其中 $x_0$ 是超平面上任意一点（即满足 $a^Tx_0=b$ 的点）。
也可以表示为：
$\lbrace x\:\vert\: a^T\left( x-x_0\right)=0\rbrace=x_0+a^{\bot},$ 其中 $a^{\bot}$ 表示 $a$ 的正交补（orthogonal complement），即与 $a$ 正交的所有向量的集合：
$a^{\bot}=\lbrace v\:\vert\: a^Tv=0\rbrace.$
在这里插入图片描述
一个超平面把空间 ${\bf R}^n$ 分成两个半空间（halfspace）,一个（封闭的）半空间是形式为 $\lbrace x\:\vert\: a^Tx\leq b\rbrace,a\neq0$ 的集合，它是凸的，但不是仿射的。

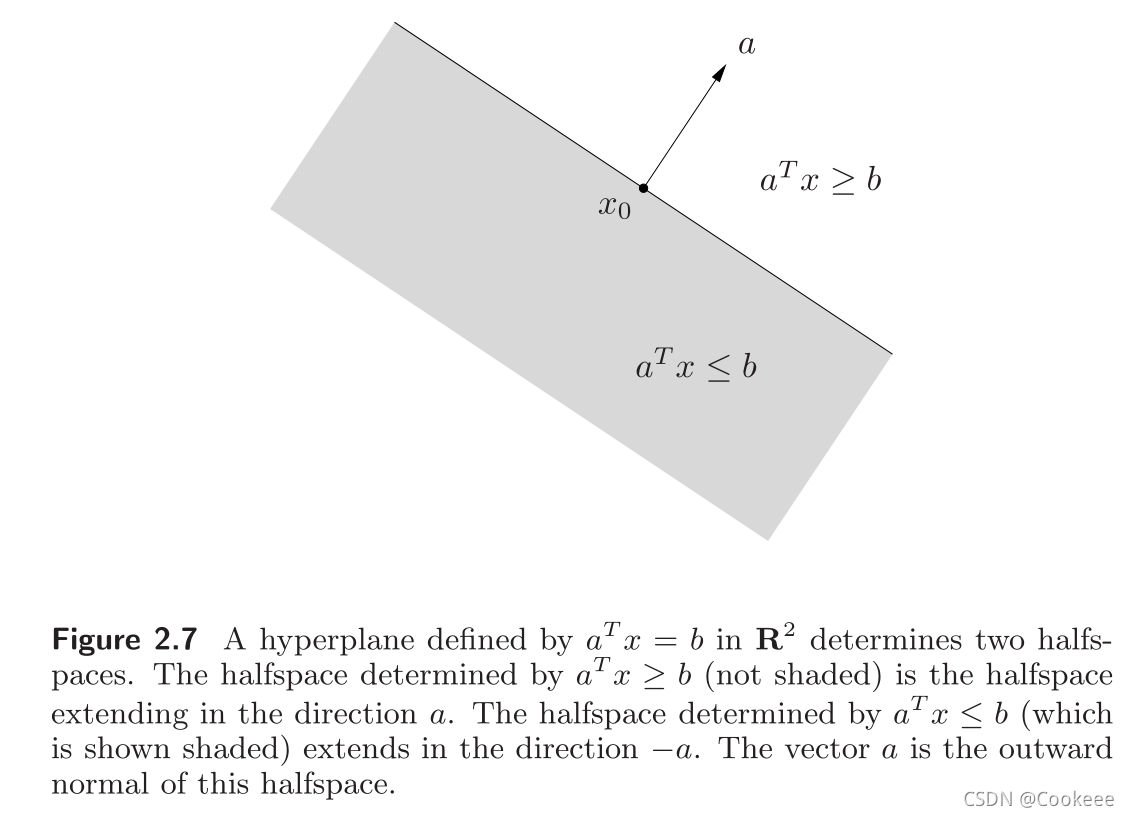
半空间由 $x_0$ 加上和向量 $a$ 夹角为钝（直）角的向量组成：
$\lbrace x\:\vert\: a^T\left( x-x_0\right)\leq0\rbrace,$
在这里插入图片描述
开半空间（open halfspace）： $\lbrace x\:\vert\: a^Tx<b\rbrace,a\neq0.$

2.2 欧几里得球（Euclidean balls）和椭球（ellipsoids）

${\bf R}^n$ 上的一个欧几里得球（或者说一个球）是形式如下的集合：
$\left( x_c,r\right)=\lbrace x \: \vert \: \lVert x-x_c \rVert_2 \leq r \rbrace=\lbrace x \: \vert \: {\left( x-x_c\right)}^T\left( x-x_c\right) \leq r^2 \rbrace,$ 其中 $r > 0$ ， $\lVert \cdot \rVert_2$ 表示欧式范数， $\lVert u\rVert_2={\left( u^Tu\right)}^{1/2}$ 。
在这里插入图片描述
这里用到了范数的性质²。
椭球体：