最短路径（包含迪杰斯特拉算法和弗洛伊德算法）

1、迪杰斯特拉（Dijkstra）算法：

Dijkstra 算法是一种用于计算单源最短路径的经典图论算法，其核心思想是：

• 从起点出发，逐步向外扩展，每次选择当前已知的最短路径顶点
• 利用该顶点更新其邻接顶点的最短路径估计值
• 通过贪心策略确保每一步选择的路径都是当前最优解

关键代码及注释如下：

#include<iostream>
#include<vector>
#include<stack>
using namespace std;
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;//存储边的二维数组
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};

void creatDGraph(MGraph& gp,int n){//创建有向图 
	int i,j;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	for(i=0;i<n;i++){
		for(j=0;j<n;j++){
			cin>>gp.arc[i][j];
		}
	}
}
void displayShortestPath(int v0,vector<int>distance,vector<int>parent){
	int n=distance.size();
	int i;
	for(i=0;i<n;i++){
		if(i!=v0){
			stack<int>path;//创建一个栈来存储路径
			int k=i;
			while(parent[k]!=k){
				path.push(k);
				k=parent[k];
			}  
			path.push(k);
			  //在栈中存储路径
			cout<<v0<<'-'<<i<<'-'<<distance[i]<<"----[";
			while(!path.empty()){
				cout<<path.top()<<" ";
				path.pop();
			}
			cout<<"]"<<endl;
		}
	}
}
void ShortestPath_Dijkastra(const MGraph&gp,int v0){//以下标为v0的点为起点 
	int n=gp.vex.size();
	int i,j;
	vector<int>parent(n);//用来存储最短路径 点的根结点 
	vector<int>distance(n);//用来存储点到v0的最短距离 
	vector<bool>find(n,false);//用来标记点是否找到最短路径 
	for(i=0;i<n;i++){
		if(gp.arc[v0][i]!=0)
			distance[i]=gp.arc[v0][i];
		 else 
		    distance[i]=0x7FFFFFFF;
		
		 parent[i]=v0; 
	} 
	parent[v0]=v0;
	distance[v0]=0;
	find[v0]=true;
	
		//主循环，每循环一次确认一个点到v0的最短路径，并且修改其他点到v0的最短路径 
	for(i=0;i<n-1;i++){
		int min=0x7FFFFFFF;
		int k=v0;
		for(j=0;j<n;j++){
		
			if(!find[j]&&distance[j]<min){
				k=j;
				min=distance[j];
			}//在还没被标记的点中确定一个到v0距离最短的点 
		}
		cout<<k;
		find[k]=true; 
		
		//接下来利用这个点来更新 其他点到v0的最短路径 
		for(j=0;j<n;j++){
			if(!find[j]&&gp.arc[k][j]!=0&&distance[j]>(min+gp.arc[k][j])){
				distance[j]=(min+gp.arc[k][j]);	
				parent[j]=k;
			}
		} 
	} 
	displayShortestPath(v0,distance,parent ) ;
	
}
int main(){ 
	int T;
	cin>>T;
	while(T--){
	
		int n;//顶点数 
		cin>>n;
		MGraph gp(n);
     	creatDGraph(gp,n);
	    int v0;
	    cin>>v0;//以下标为v0的点为起点找最短路径 
	    ShortestPath_Dijkastra(gp,v0);
	}
	return 0;
} 

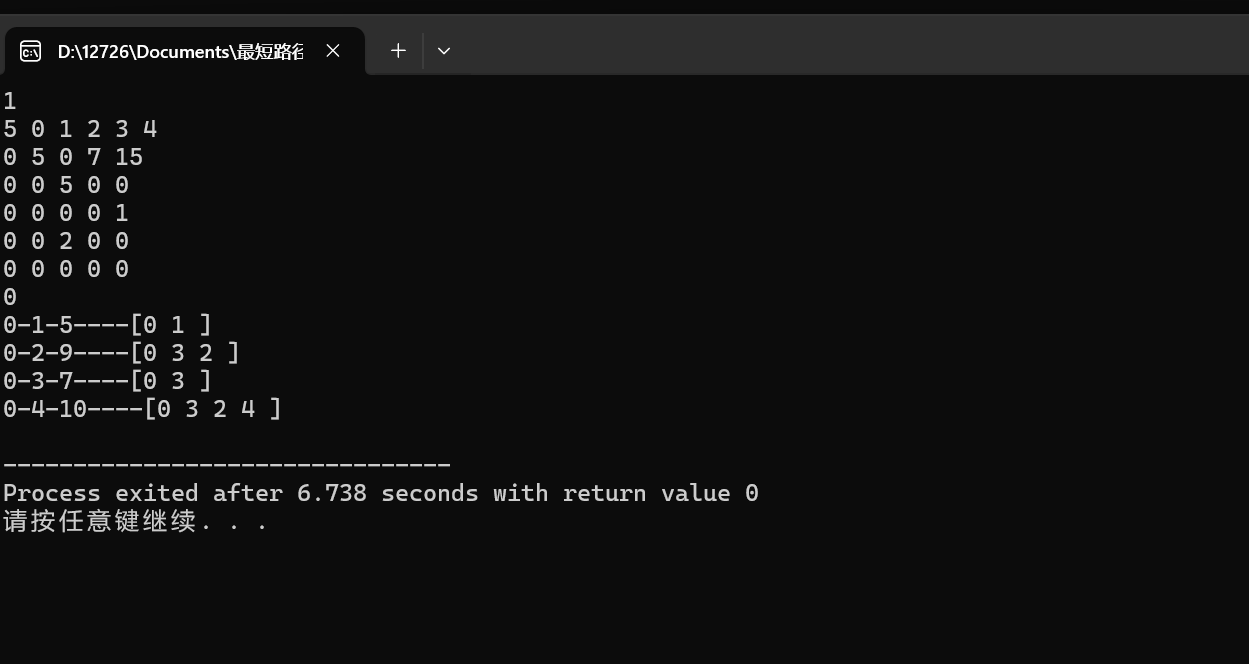
 输入输出如下：

 2、Floyd(弗洛伊德)算法:Floyd 算法是一种用于计算多源最短路径的经典图论算法

代码实现关键点

1. 图的表示：使用邻接矩阵 arc 存储边的权重，0x7FFFFFFF 表示无穷大（不可达）。
2. 距离矩阵 distance：初始化为邻接矩阵，逐步更新为最短路径长度。
3. 前驱矩阵 path：path[i][j] 记录从 i 到 j 的最短路径上的第二个顶点，用于路径重建。
4. 三重循环：
   • 外层循环遍历中间顶点 i。
   • 内层两层循环遍历所有顶点对 (j, k)，检查是否通过 i缩短路径

 我把我对该算法的一些理解在以下代码中进行了注释

#include<iostream>
#include<vector>
#include<stack>
using namespace std;
struct MGraph{
	vector<char>vex;
	vector<vector<int> >arc;//存储边的二维数组
	MGraph(int n){
		vex.resize(n);
		arc.resize(n);
		int i;
		for(i=0;i<n;i++){
			arc[i].resize(n);
		}
	}
};

void creatDGraph(MGraph& gp,int n){//创建有向图 
	int i,j;
	for(i=0;i<n;i++){
		cin>>gp.vex[i];
	}
	for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            cin >> gp.arc[i][j];
            if (i != j && gp.arc[i][j] == 0) {
                gp.arc[i][j] = 0x7FFFFFFF;
            }
        }
    }
}

//展示所有最短路径 
void showShortestPath(const MGraph& gp,const vector<vector<int> >&distance,const vector<vector<int> >&path){
	int n=distance.size();
	int i,j;
	for(i=0;i<n;i++){
		for(j=0;j<n;j++){
			if(i!=j){
				cout<<gp.vex[i]<<"-"<<gp.vex[j]<<":"<<distance[i][j]<<endl;
			    cout<<gp.vex[i]<<"-";
			
			    int k=path[i][j];
			    while(k!=j){
			    	cout<<gp.vex[k]<<"-";
			    	k=path[k][j];
		    	}
		    	cout<<gp.vex[j]<<endl;
				
			}
			
		}
	}
}
void ShortestPath_Floyd(const MGraph& gp){
	int i,j,k;
	int n=gp.vex.size();
	vector<vector<int> >distance(n,vector<int>(n));//存储距离的二维数组 
	vector<vector<int> >path(n,vector<int>(n));  //对应顶点最短路径的前驱矩阵  
	
	for(i=0;i<n;i++){
		for(j=0;j<n;j++){
			distance[i][j]=gp.arc[i][j];
			path[i][j]=j;      //初始化 distance和path (path可以理解为从i到j路径上的第二个地点)
		}
	}
	
	//以下是主循环
	for(i=0;i<n;i++){  //最外层循环分别以不同的点为中心点 
		for(j=0;j<n;j++){
			for(k=0;k<n;k++){
				if(distance[j][k]>distance[j][i]+distance[i][k]&&(distance[j][i]+distance[i][k])>0){
					distance[j][k]=distance[j][i]+distance[i][k];
					path[j][k]=path[j][i];     //修改path改变前驱，让 path[j][k]始终表示 j到k路径上的第二个地点
				}
			}
		} 
		
	}
	showShortestPath(gp,distance,path);
}

int main(){ 
	int T;
	cin>>T;
	while(T--){
	
		int n;//顶点数 
		cin>>n;
		MGraph gp(n);
     	creatDGraph(gp,n);
	    
	    ShortestPath_Floyd(gp);
	}
	return 0;
} 

 输入输出如下：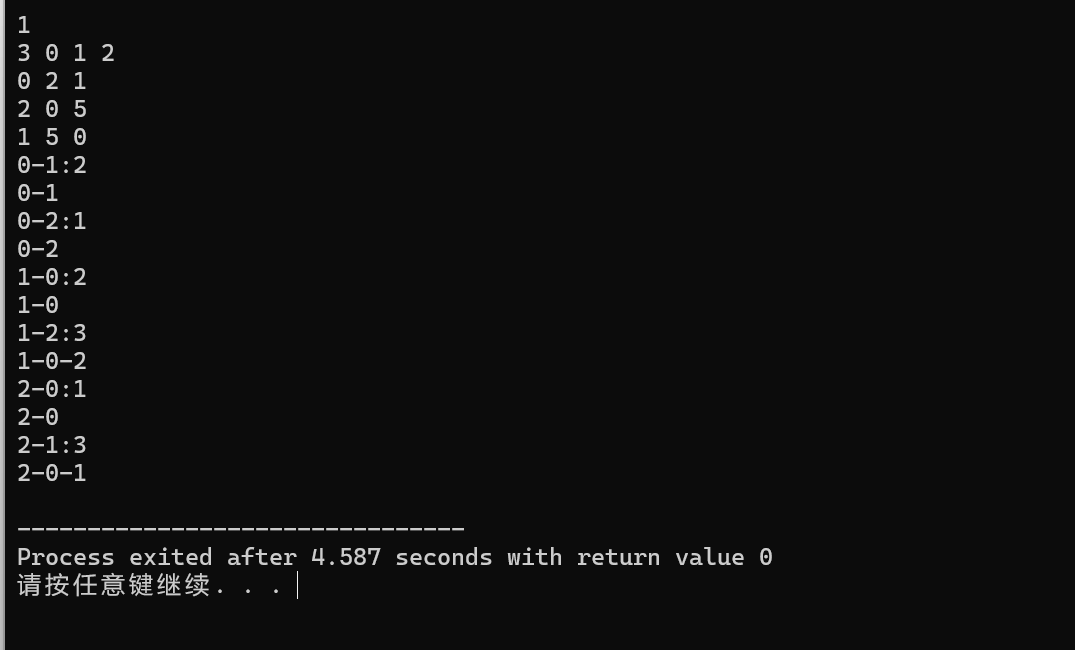

 我在写代码的时候遇到了一个bug,因为我用0x7FFFFFFF表示最大距离即不连通的点，而在后续的相加中导致int型越界变为负数，解决办法是通过(distance[j][i]+distance[i][k])>0来确保不越界