104. 二叉树的最大深度【二叉树】

104. 二叉树的最大深度

104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

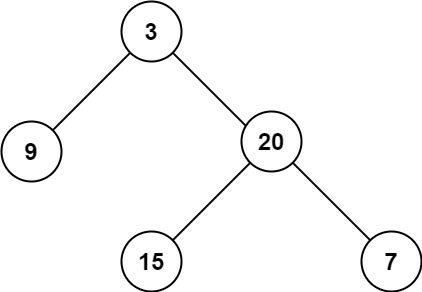
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 10^4] 区间内。
• -100 <= Node.val <= 100

解法一：层序遍历

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 层序遍历，层数就是最大深度
    queue := make([]*TreeNode,0)
    queue = append(queue,root)
    res := 0
    for len(queue) > 0 {
        queueSize := len(queue)
        for i := 0;i < queueSize;i++ {
            curNode := queue[0]
            queue = queue[1:]   
            if curNode.Left != nil {
                queue = append(queue,curNode.Left)
            }
            if curNode.Right != nil {
                queue = append(queue,curNode.Right)
            }
        }
        // 遍历完一层后，层数+1
        res += 1  
    }

    return res
}

解法二：深度递归法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 使用前序遍历，不断更新最大深度的变量值
    res := 1
    dfs(root,1,&res)
    return res
}

func dfs(root *TreeNode,depth int,res *int)  {
    if *res < depth { // 中
        *res = depth
    }

    if root.Left != nil { // 左
        depth += 1 // 深度+1
        dfs(root.Left,depth,res)
        depth -= 1 // 回溯，深度-1
    }

    if root.Right != nil { // 右
        depth += 1 // 深度+1
        dfs(root.Right,depth,res)
        depth -= 1 // 回溯，深度-1
    }

}

解法三：粗暴递归法

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 这里实际是后续遍历（左右根），不过用一行写了，实际可以改成如下四行
    // leftDepth := maxDepth(root.Left) // 左
    // rightDepth := maxDepth(root.Right) // 右
    // 根（遍历到根时就是具体的处理逻辑，遍历到左右节点时则是递归）
    // curNodeDepth = max(leftDepth,rightDepth) + 1 
    // return curNodeDepth
    return max(maxDepth(root.Left),maxDepth(root.Right)) + 1
}

func max(a,b int) int {
    if a > b {
        return a
    }

    return b
}