【Transformer】三、Transformer原论文的背景与核心创新

前言

《Attention is All You Need》论文地址：https://arxiv.org/abs/1706.03762

通过前面的两篇文章，我们知道《Attention is All You Need》的两个核心创新点是： Transformer 架构和 Self-Attention自注意力机制

那么为什么这两个创新会带来革命性的突破呢？换句话说，在2017年这篇论文出现之前，为什么没有迎来大语言模型时代？

为了搞清楚这个问题，我们就需要知道以往的一些模型结构是什么样的，它们都存在着什么样的瓶颈。从而进一步的理解Transformer做了哪些创新，解决了什么样的难点，以及为什么Transformer能突破这些瓶颈或者限制。

在Transformer论文的摘要中出现了一个词，序列转导模型（Sequence Transduction Model），那么什么是序列转导模型（Sequence Transduction Model）呢？我们就以它入手吧。

一、序列转导模型（Sequence Transduction Model）

序列转导模型（Sequence Transduction Model）是处理序列数据的模型

• 序列数据：具有顺序关系的数据，每个元素的顺序对于数据的整体含义非常重要
• 典型的序列转导模型
  • 文本翻译：翻译前的文本(“How are you”) -> 翻译后的文本（“你好吗？”）；
  • 文本生成：用户的输入文本(“How are you?”) -> AI生成的回复文本(“I’m fine, thank you.”)；
  • 语音转文字：一个音频片段 —> 音频的文字转写；

Transformer出现之前，这些序列转导模型，主要是复杂的卷积神经网络（CNN）和循环神经网络（RNN）。由此，我们知道主流序列转导模型的结构发展如下：

Transformer之前

1. 基于RNN/CNN
2. 使用编码器-解码器结构
3. 使用注意力机制增强

Transformer结构的创新:

1. 完全摒弃RNN/CNN
2. (仍然使用编码器-解码器构)
3. 完全基于注意力机制

为了更好的理解Transformer，让我们先来看一些以往的模型结构以及他们的不足吧。

1.1 前馈神经网络 Feedforward Neural Network（FNN）

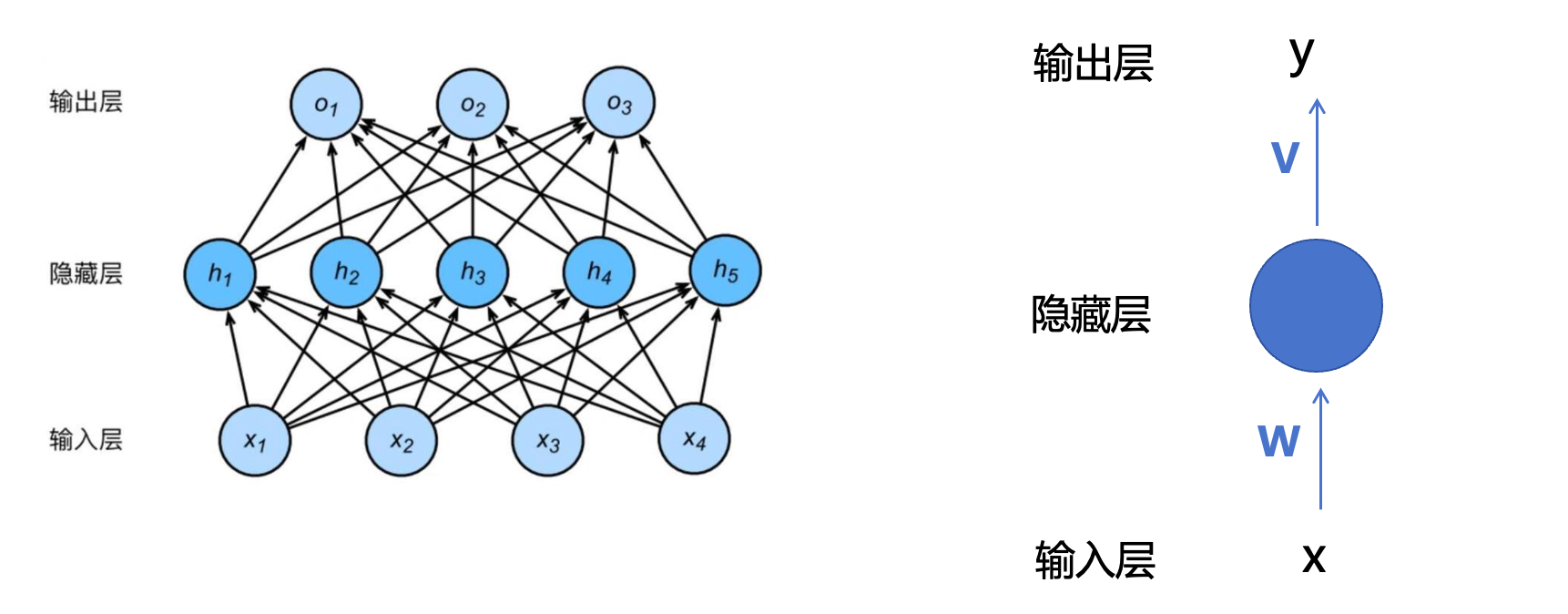
在学习深度学习的时候，FNN是大家接触到的最基本的神经网络，X为输入，Y为输出，W和V分别为对应层的权重矩阵，具体细节这里不过多说明了，主要想探讨一下为什么FNN就不适合做序列转导任务呢？

让我们看一个例子：

输入：水是有毒的

步骤一：分词（Tokenization）
[“水”, “是”, “有毒”, “的”]

步骤二：词向量表示（Embedding）

“水” → [0.2, -0.1, 0.3, 0.0]

“是” → [0.0, 0.5, -0.2, 0.1]

“有毒” → [0.9, -0.3, 0.4, 0.2]

“的” → [0.1, 0.0, 0.0, 0.1]

步骤三：合并词向量（平均或拼接）

• 平均：将上面四个向量对应位置相加后取平均值，最有得到一个新的1*4的向量，这种方式完全丢掉了词语的顺序。

• 拼接：将上面四个向量收尾相连，变为一个1 * 16的向量。

  • FNN 需要固定维度的输入，对不同长度的句子处理效率低下,比如上图中的FNN接受的收入是x1~x4一个四位的向量，而现在我们是一个1*16的向量，它是处理不了的，除非我们将FNN的输入变为16维或更高维度（大于16的位置补0），但这样的处理方式，如果想要应对非常长的句子，我们就得事先将FNN的属于定义的维度非常高，但是平时更常见的场景是处理短句，后面补很多0，处理效率低下。
  • 仍然会将句子视作一个整体来处理，无法理解真正的“谁先谁后”的关系。

1.2 循环神经网络 Recurrent Neural Network (RNN)

由于前馈神经神经网络FNN在处理时序转导模型时，存在以上的一些不足，因此后续诞生了循环神经网络 Recurrent Neural Network (RNN) 。

首先我们看一下RNN解决了什么问题：

1. 能够建模词序：RNN 是按时间顺序（token 顺序）逐个处理输入的；
2. 能够建模上下文依赖：RNN 是逐个喂入词语，并且会有“记忆”机制；
3. 支持不定长输入：不再需要 FNN 那种固定长度的输入格式，句子多长都行；

RNN相对CNN在处理时序信息时有以上三个优势，那RNN是如何达到以上效果的呢？

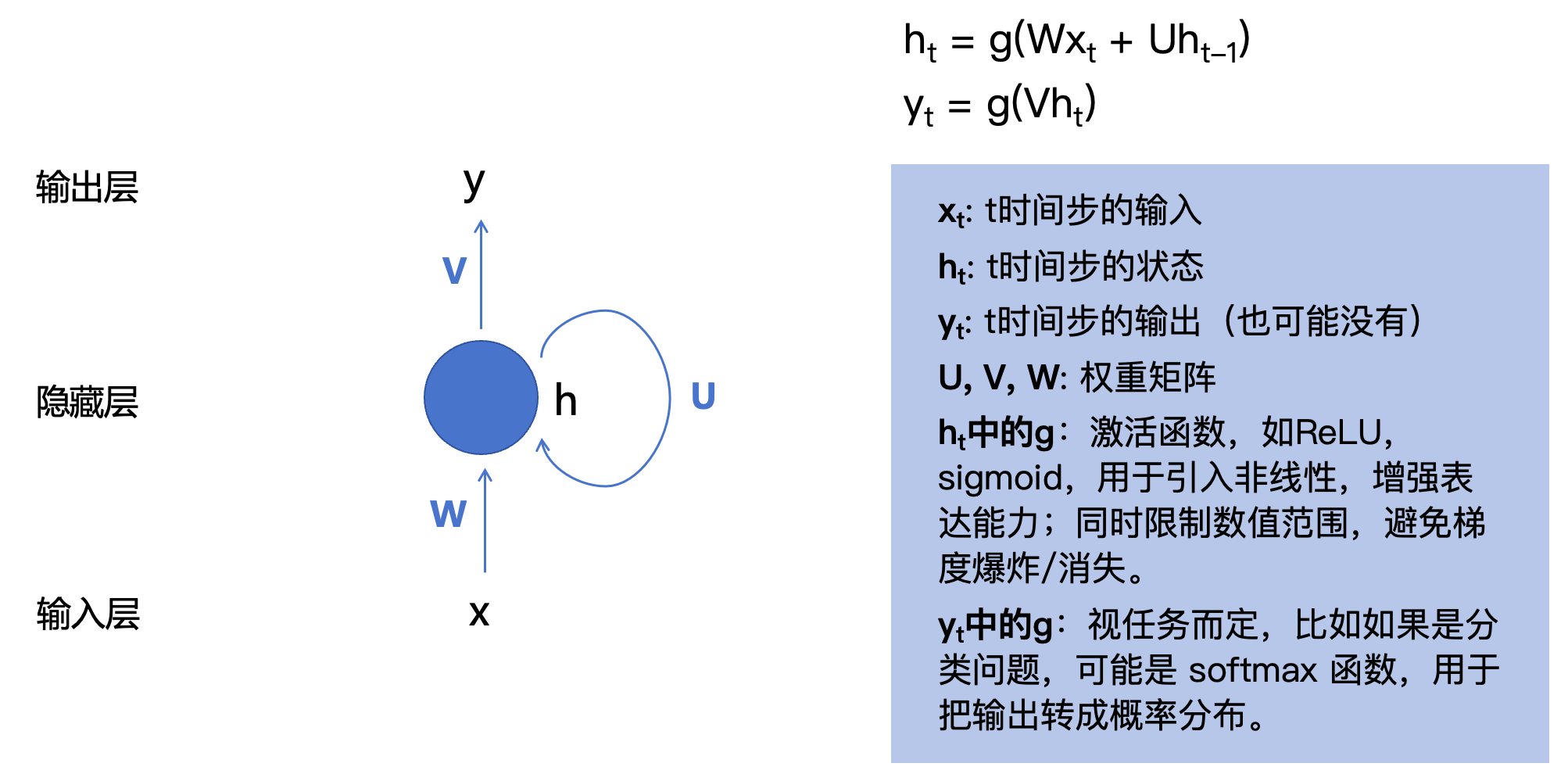
可以看到RNN其实也并不复杂，不过是在FNN的基础上加了h位置的一个圈（循环）。

• 输入$X$不再表示为$x_n$，而是表示为$x_t$，因为RNN的输入是时序的，每次输入一个时序值，

• $x_t$: t时间步的输入

• $h_t$: t时间步的状态，$h_t=g(W{x}_t+U{h}_{t-1})$

• $y_t$: t时间步的输出（也可能没有）$y_t=g(V\ast h_t)$

• $U,V,W$: 权重矩阵

• $h_t$中的$g$：激活函数，如$ReLU，sigmoid$，用于引入非线性，增强表达能力；同时限制数值范围，避免梯度爆炸/消失。

• $y_t$中的$g$：视任务而定，比如如果是分类问题，可能是 $softmax$ 函数，用于把输出转成概率分布。

对于“我爱水课”这句话，【我】将作为第一个token，即$x_1$进行输入，处理完成后，【爱】作为第二个token进行输入，这便是时序输入。让我们将其过程进行展开：

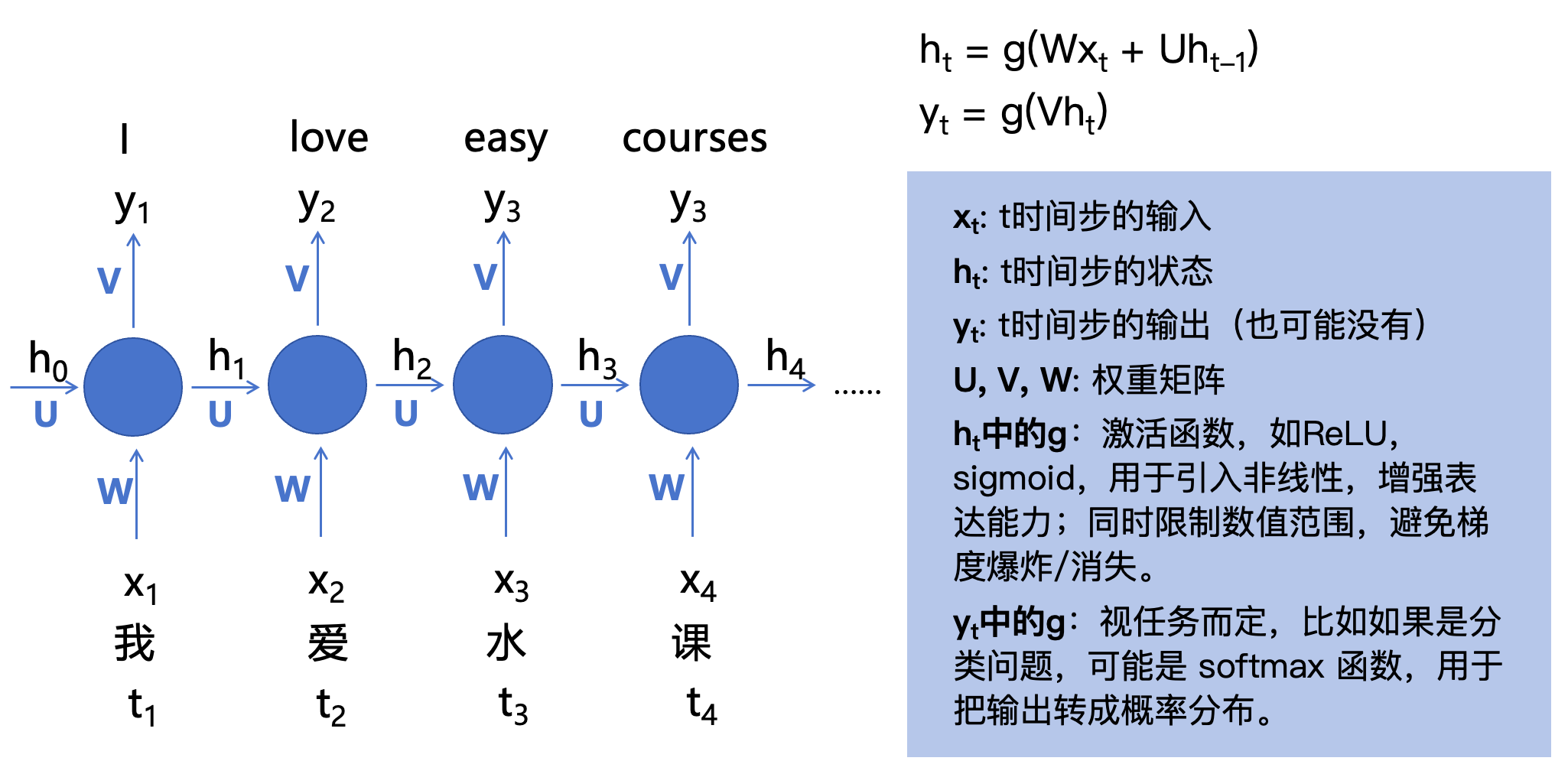
$h_0$是我们初始化的参数，$x_1$是$t_1$时刻的输入：【我】，进行运算后得到了第一个输出$y_1$,而中间状态$h_1$,将参与下一个时刻的输入计算，即：
$$\begin{gathered} h_1=g(W\ast x_1+U\ast h_0) \\ {y}_1=g(V\ast h_1) \\ {h}_2=g(W\ast x_2+U\ast h_1) \\ {y}_2=g(V\ast h_2) \\ ... \end{gathered}$$

从上图以及公式可以看到一下信息：

• 对于一个时刻的输入会有两个输出，一个是$y_t$，对于时刻$t$输入的输出，一个是$h_t$,是对于$t$时刻输入的中间态，会参与后续时刻的计算。
• $h_1$不仅参与了$y_1$的计算，也参与了$h_2$的计算，也就是前一个时刻计算的中间状态会参与下一个时刻的计算，正式由于这个依赖，后续时刻的输入因为依赖了前置时刻输入的中间态$h_t$，从而导致了无法并行计算。
• 为什么$W，U，V$矩阵在上面公式中不用表示为$W_t,U_t,V_t$，比如$W_1,W_2$等，因为上图是将多个时序计算进行了展开方便理解，从而让我们以为有多个$W，U，V$的错觉，但实际上对于每一个时序的计算，W，U，V矩阵都是一模一样的，就是在循环针对每个时序输入进行计算，所以不用带下标区分。

至此，我们知道了RNN可以解决FNN在处理时序任务时的一些瓶颈问题（能记住输入的顺序，后续输入能知道前置时刻输入的上下文）

但是RNN也有自身的一些局限性

• 输入输出不等长时怎么办？
• 无法并行计算，训练效率低

1.3 编码器 - 解码器结构 Encoder and Decoder

可以简单的理解下图：将RNN的上半部分和下半部分分开做

• Encoder : RNN的下半部分，将所有时序输入进行编码，计算出最后一个中间状态$h_4$，也就是上下文C，他包含了整个时序输入的上下文信息。
• Decoder: RNN的上半部分, 对上下文C进行解码输出操作，注意：前一个输出(如下图I）以及前一个输出的中间态（如下图S1），都会作为下一个时序的输入参与计算。下图中的S0就是C，即C作为了解码器的原始输入。
  

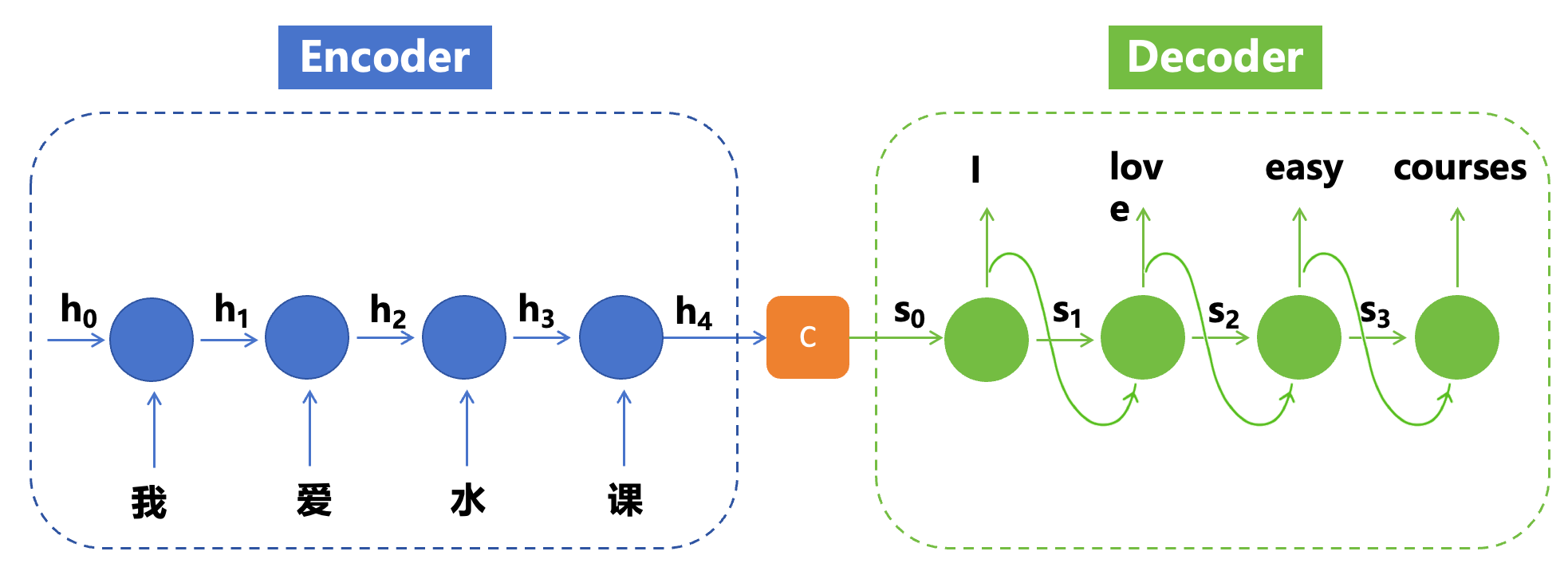
编码器的输出C：上下文向量（context vector）

• 它是对整个输入序列的语义编码，是一个固定长度的向量，涵盖了整个输入文本的语义信息，同时也隐式的包含了输入序列的顺序（位置）信息，因为是一个一个时序输入循环计算得来的C，输入时序不一样，得到的C会不一样的。
• 最简单的编码方式：C = 最后一个时间步的隐藏状态输出(h4)
• 它将作为 Decoder 的输入，用于生成目标序列。

由于解码到靠后为止的时候，相关信息可能已经被稀释的差不多了，会丢失一些较早信息的特征情况，所以我们又想到了一种方式，给每一个解码器的时间步再输入一次上下文C，如下图：

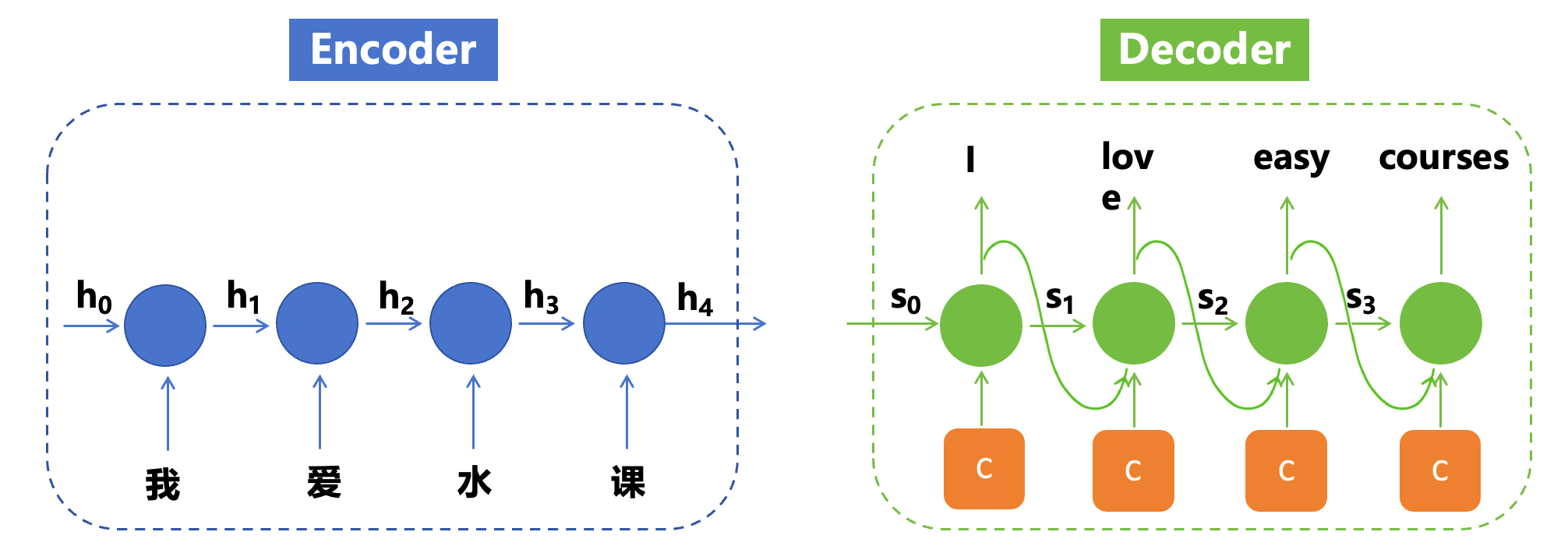
但是这种方式也有缺陷：所有时间步的输入在计算当前时刻输出时被同等对待，忽略了不同时间步对当前时刻输出的重要性可能存在的差异。由此引出了注意力机制。

1.4 传统注意力机制

注意力机制解决的问题：

1. 解决模型处理长序列时的“遗忘”问题：随着序列长度的增长，远距离依赖信息在传递过程中易被稀释，导致模型对长距离依赖关系的建模能力减弱。

2. 解决不同时间步输入对当前时刻输出的“重要性”问题：所有时间步的输入在计算当前时刻输出时被同等对待，忽略了不同时间步对当前时刻输出的重要性可能存在的差异。

比如下图，我们将上下文C又作为了解码器每个时序解码时的一个输入，而我们知道C是$h_4$，$h_4$计算的时候肯定是受离它进的一些时序输入token比较大（如$x_3$)，而离它更远的token因为进行了多层的计算和稀释，可能已经被稀释的差不多了。

那么我们希望解码器的每个时间步可以关注到上下文C中不同的重点，因此这个C对于解码器的每个时间步不能再是相同的了。

此时就因为了基础的注意力机制（注意这个和Transformer中的自注意力机制Q，K，V含义是不同的，不过他们两者的思想是一致的，期望当前token可以关注到上下文中的不同重点）

传统注意力机制基本都是与RNN一起使用，将RNN的时序输入对应的输出进行加权求和得到新的输出，步骤如下

• 一个输入序列，记为$X$，它由$t$个元素组成($t$个时序输入），分别表示为$x^{(1)}$到$x^{(t)}$。

• 注意力分数 $w$=词元$x^{(n)}$与其他词元的点积而得；点积值越大则这两个词元相似度越高（即对齐度越高）

• 嵌入化词元序列之间的注意力权重 $\alpha$= 注意力分数$w$的归一化

• 注意力分数归一化$softmax$后得到每一个词元的注意力权重$\alpha$，即获得总和为1的注意力权重

• 最后上下文向量$Z(n)=Sum$(所有$x^{(i)}$的注意力权重$\alpha$ * 嵌入化词元本身的矩阵)，即注意力权重和词元嵌入矩阵相乘后，再求和。

• 位移词元下标$i$，循环以上步骤，将所有词元的注意力权重都计算出来。

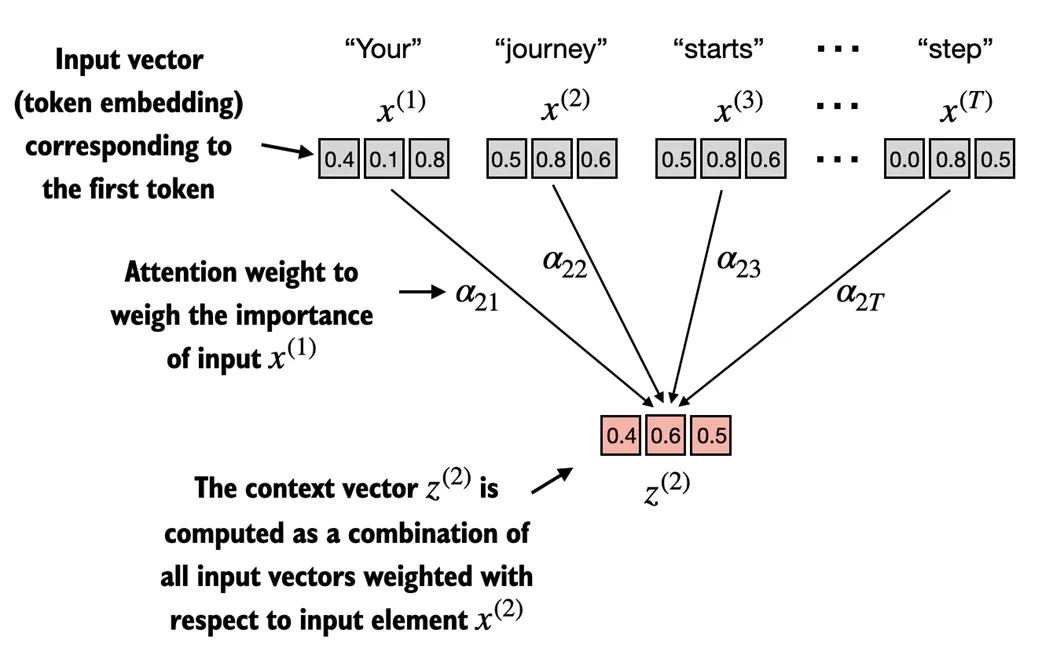
图中是列举$i=2$的此词元注意力上下文向量。

1. 注意力分数 $w=词元x^{(2)}$与其他词元（包括自身）的点积而得，（两个向量点击得到一个数值标量，所以这里与每个词元点积将得到t个标量，可以组成一个维度为t的向量）；点积值越大则这两个词元相似度越高（即对齐度越高）
2. $注意力权重\alpha =注意力分数w的归一化$，第一步中的 $t$ 维向量经过$softmax$归一化，得到每个词元对于词元$x^{(2)}$的注意力权重$a_{21},a_{22},....a_{2t}$（他们的和为1）
3. 最后上下文向量$Z(2)=x^{(1)}\ast a_{21}+x^{(2)}\ast a_{22}+...+x^{(}t)\ast a_{2t}$。
   

上面仅以$C_2$进行了举例，实际通过以上步骤，我们就可以得到所有的$C_i$，从而解码器将变为如下形式，每个解码时间步不再关注同一个整体上下文$C$，而是关注注意力算出来的$C_i$

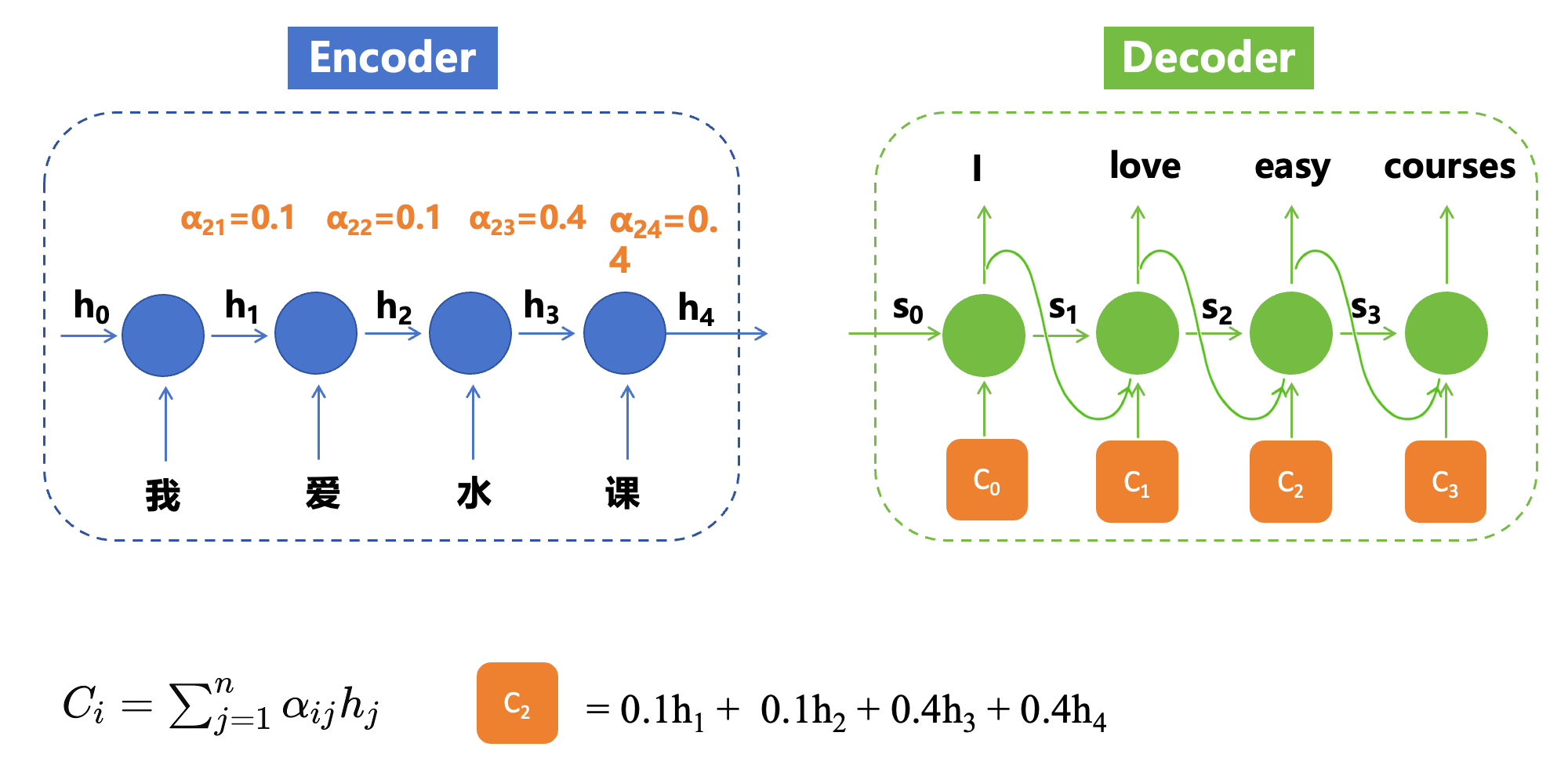
到此为止，我们解决了容易遗忘远距离时候输入的问题，那么还有什么问题没有解决呢？

• 并行计算能力：RNN 的时序依赖特性导致无法充分利用 GPU 并行能力(即RNN模型中，一句话的每个词是按时间顺序输入的，前一个词计算完之后，将其隐藏状态继续和下一个输入的词计算，如此循环，因此得名循环神经网络，而Transformer是一次性输入的一句话），Transformer 的并行处理能力使其能够高效利用现代硬件资源。

在进入Transformer前，我们先来小结一下：

RNN

• 能够建模词序(因为是时序输入）
• 能够建模上下文依赖（前面时序的隐藏状态会作为后面时序输入的一部分）
• 支持不定长输入(因为是时序输入）

编码器-解码器

• 支持输入输出不等长（编码器将所有输入信息编码为一个上下文向量，解码器对齐进行解码输出）

注意力机制

• 解决处理长序列时的“遗忘”问题
• 解决不同时间步输入对当前时刻输出的“重要性”问题

Transformer

• 解决串行化计算问题

二、Transformer

Transformer 的自注意力机制是“全局互相关注”，完全摆脱了序列结构，支持并行，是最底层的范式改变。

【Transformer】二、Transformer架构原理通识