车-电-路网时空分布负荷预测研究（Matlab代码）

👨‍🎓 个人主页： 研学社的博客

💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥


🏆 博主优势： 🌞 🌞 🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

📋 📋 📋 本文目录如下： 🎁 🎁 🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现

💥1 概述

电动汽车作为交通工具和移动负荷的载体，其出行分布和路径规划会受到交通信息的影响，而充

电需求和充电策略会影响电网经济性与安全运行，因此建立图1所示的路网-配电网-车网交互模型分析EV充电负荷的时空分布。

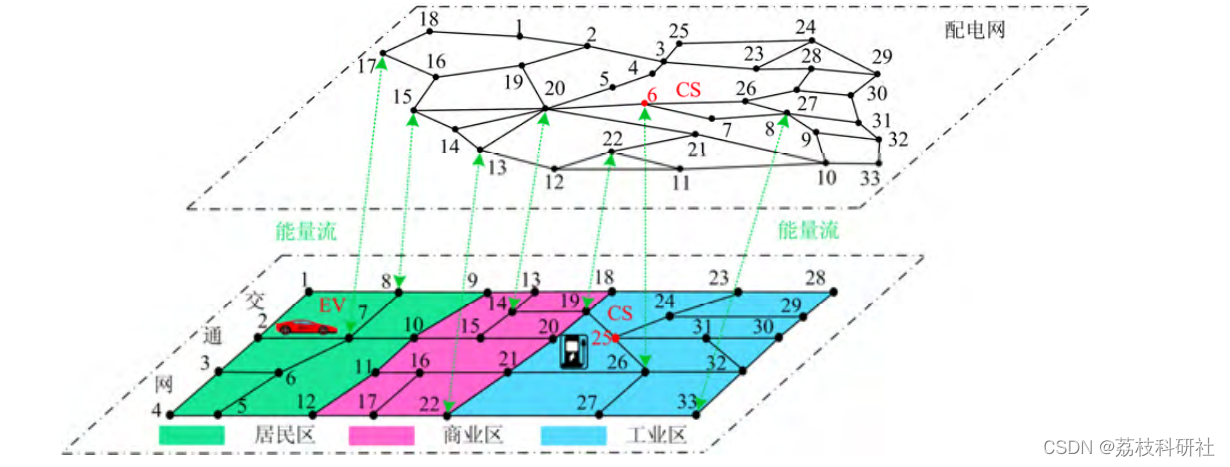
在建立各个模型后，下图给出了充电负荷时空分布预测具体流程。

由图3可知，充电负荷时空分布预测流程如下。

1) 首先按一定比例在各交通节点引入不同类型电动汽车数量；

2) 通过蒙特卡洛模拟为各EV随机抽样生成相应的行驶特性参数和充电特性参数；

3) EV用户按照行程时间最小为目标，采用实时Dijkstra算法规划的路径进行行驶，并实时更新特性

参数；

4) 通过用电区域功能类型划分，对该区域充电的EV功率进行累加计算得到区域配网节点负荷，完

成整体充电负荷时空预测。

📚2 运行结果

运行视频：

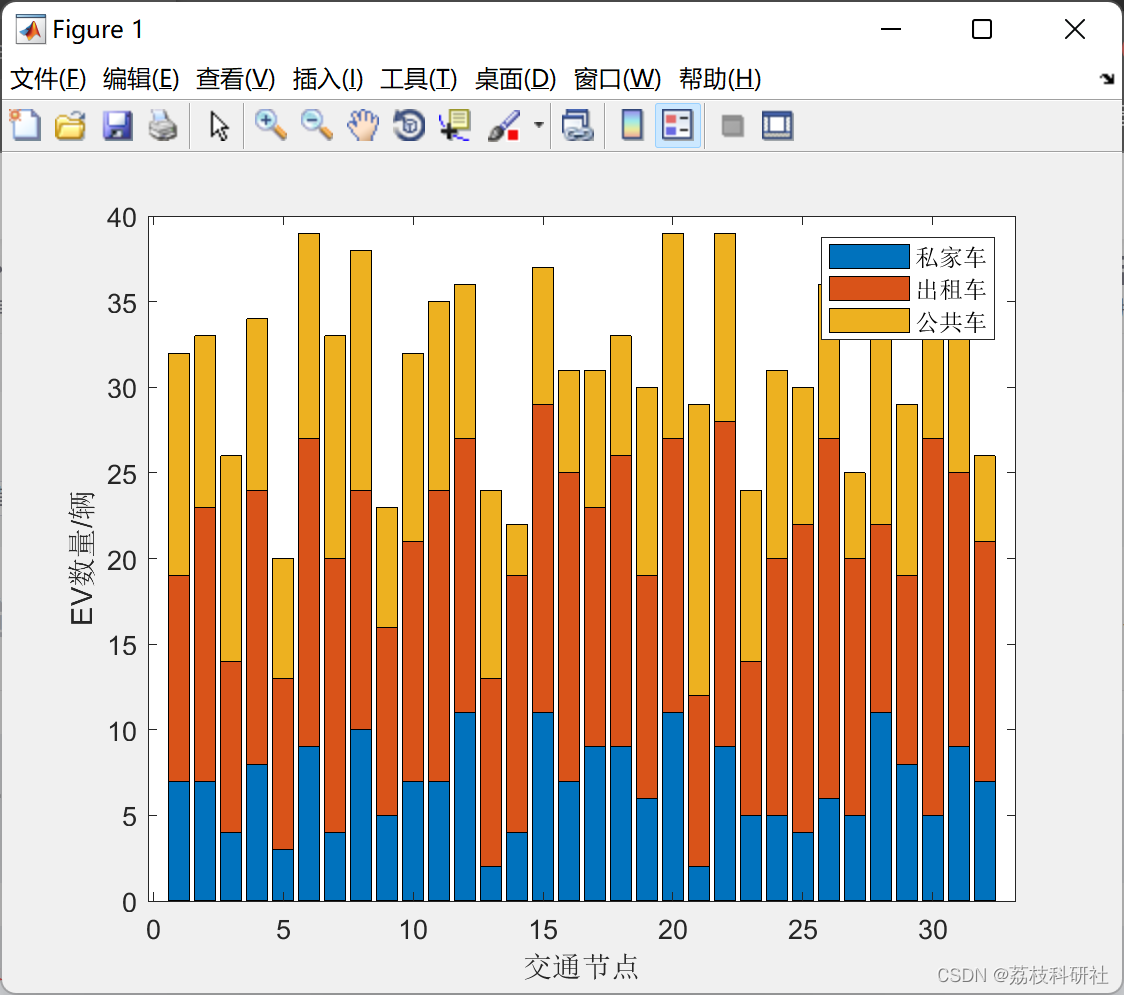
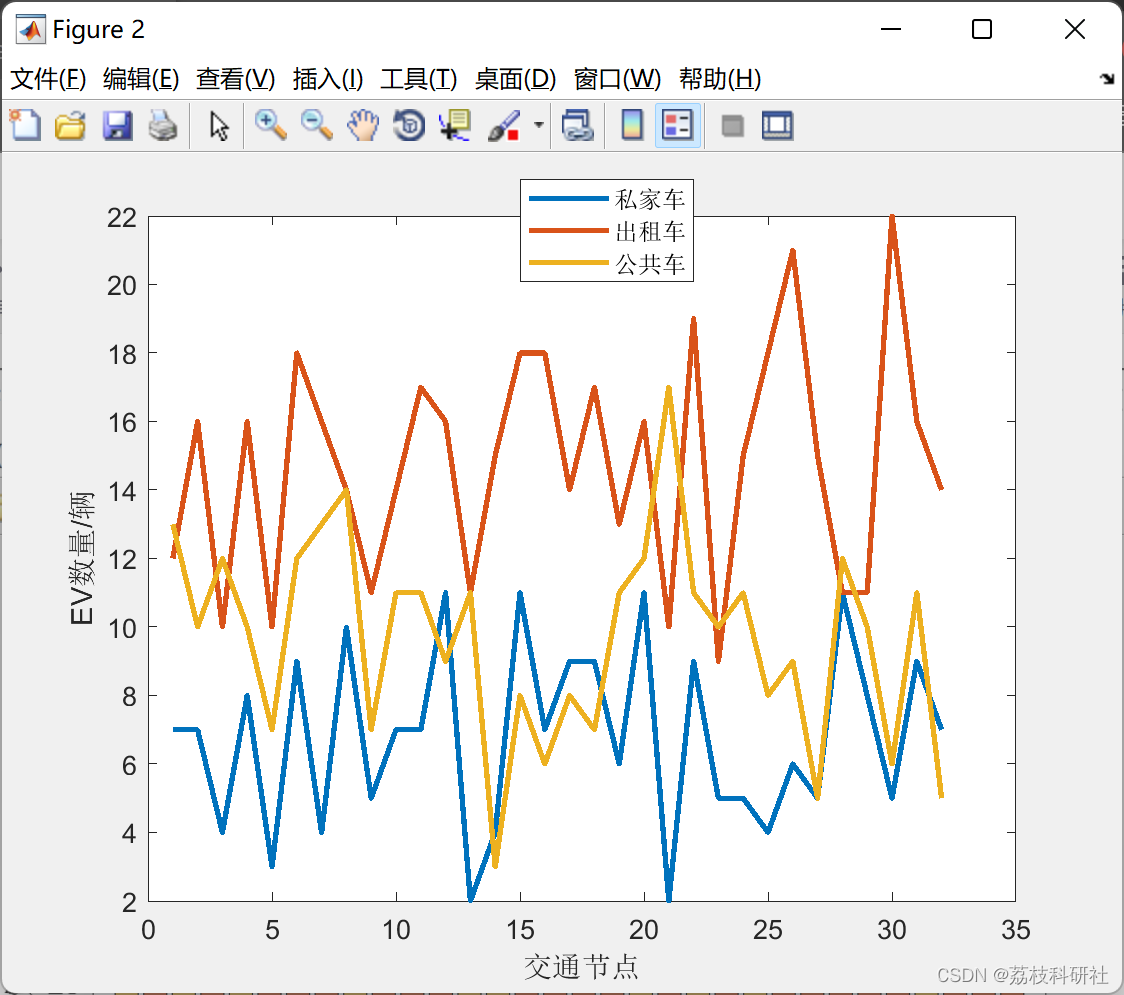
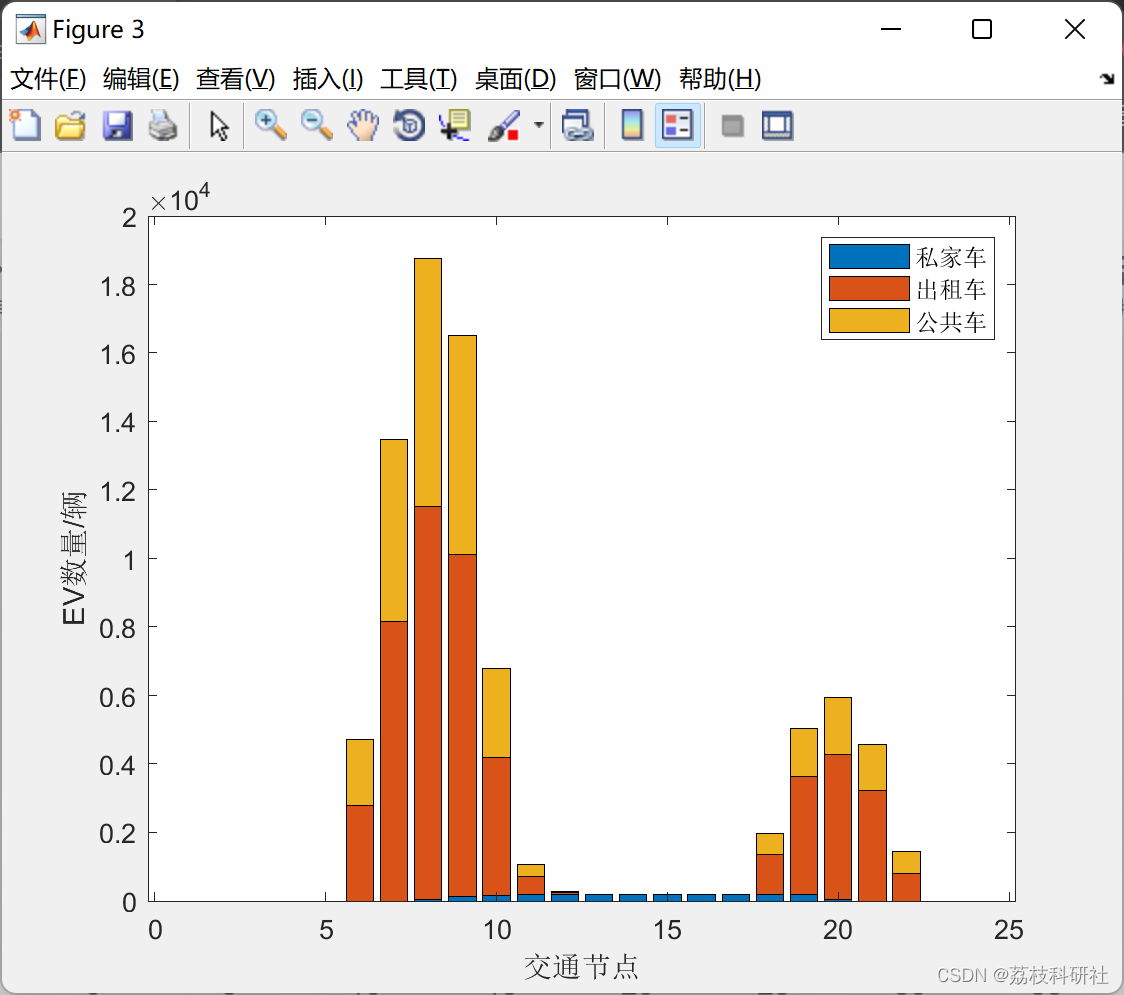
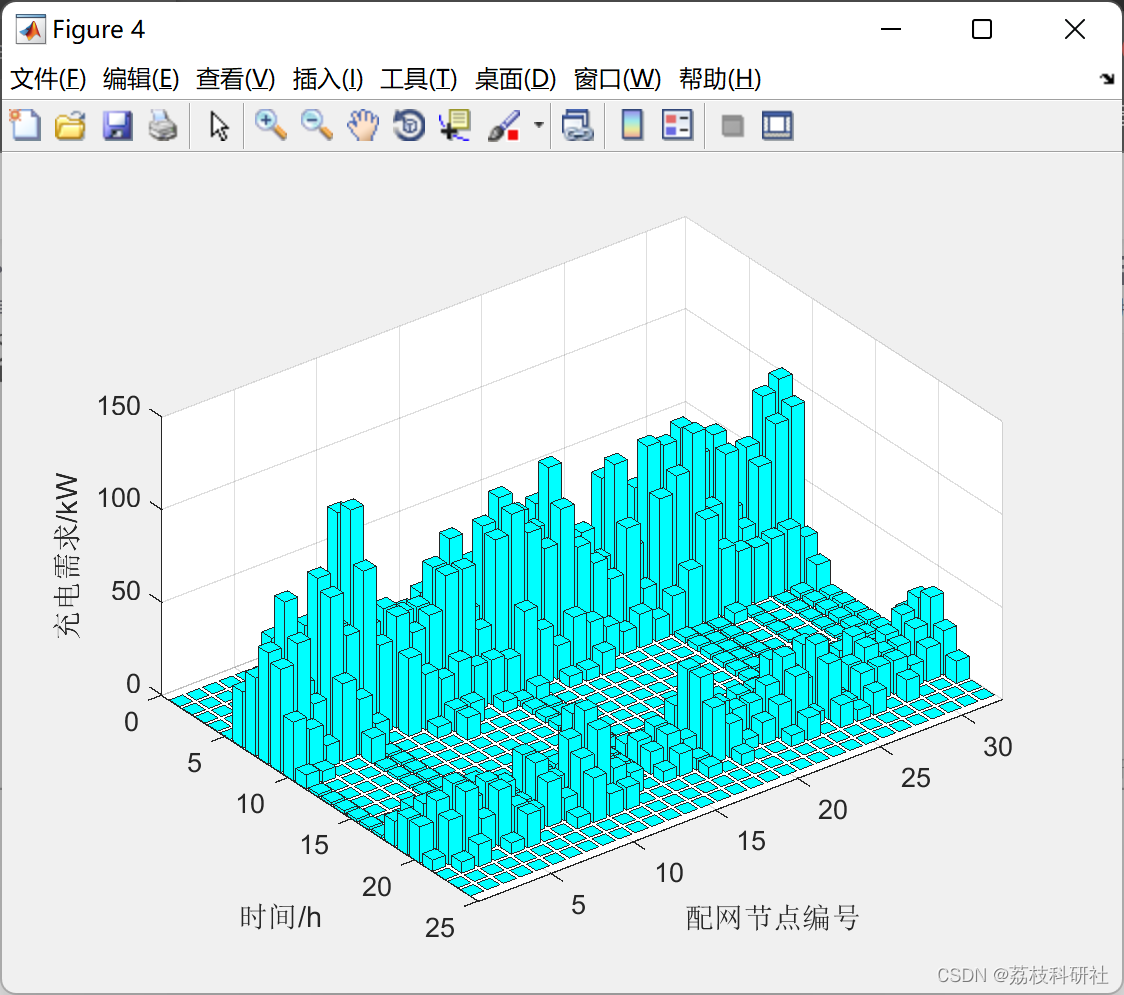
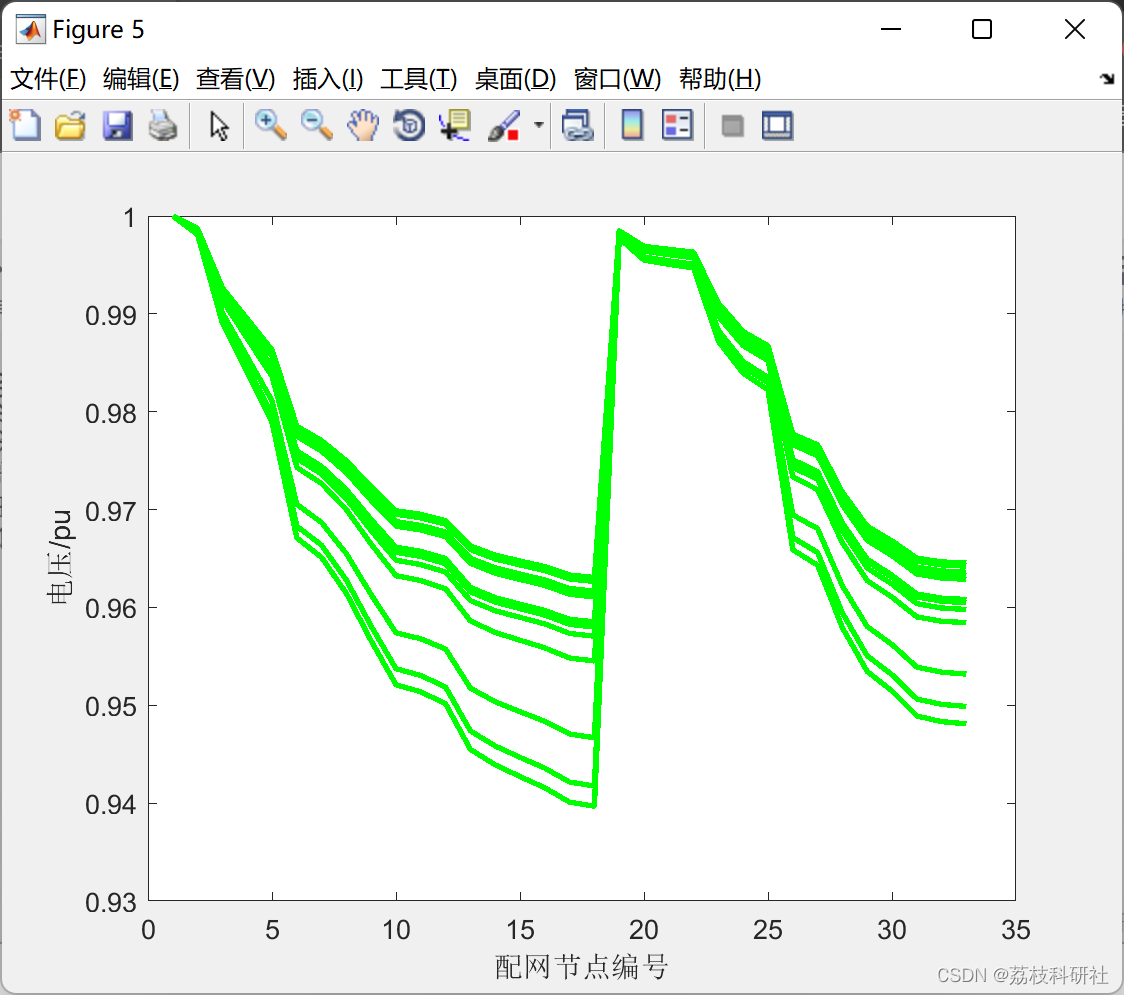
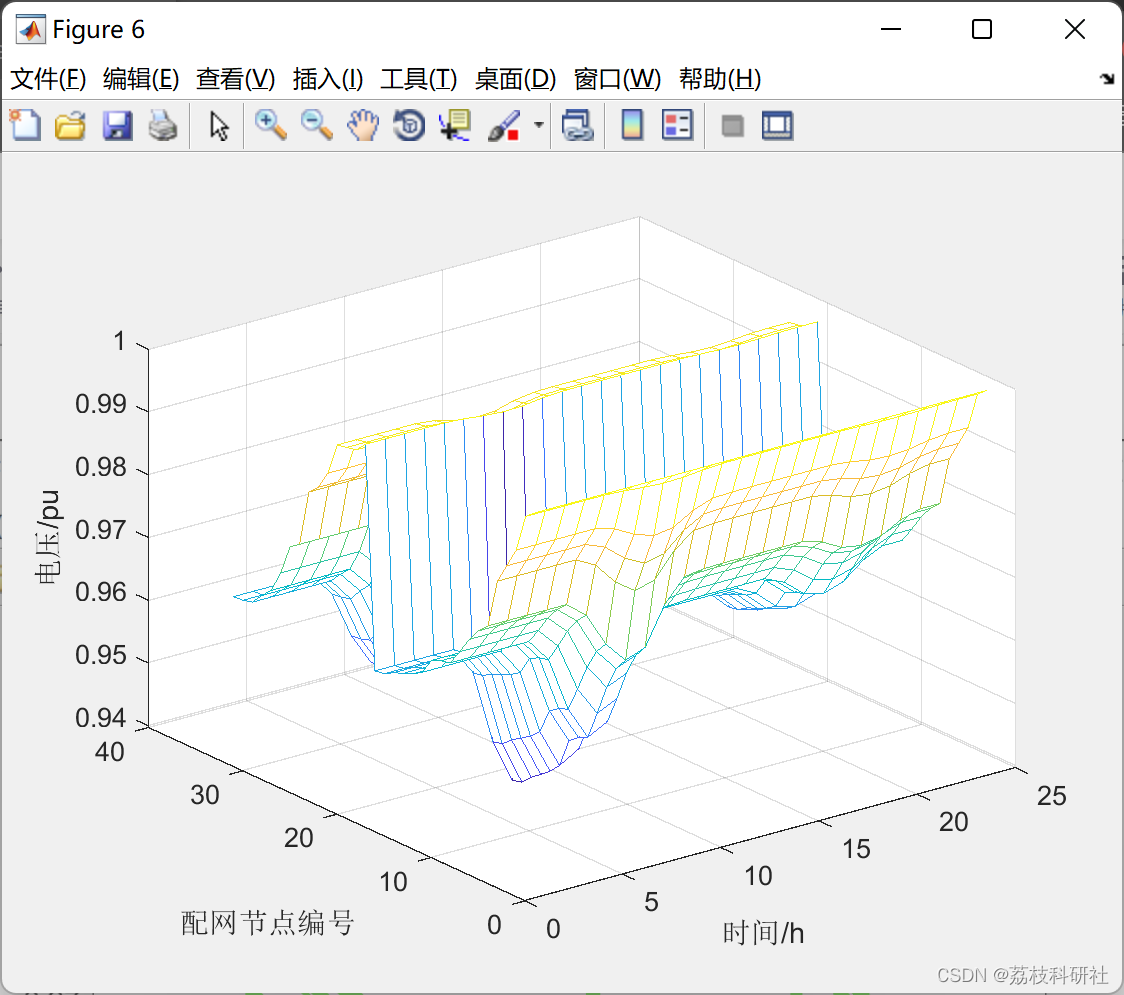
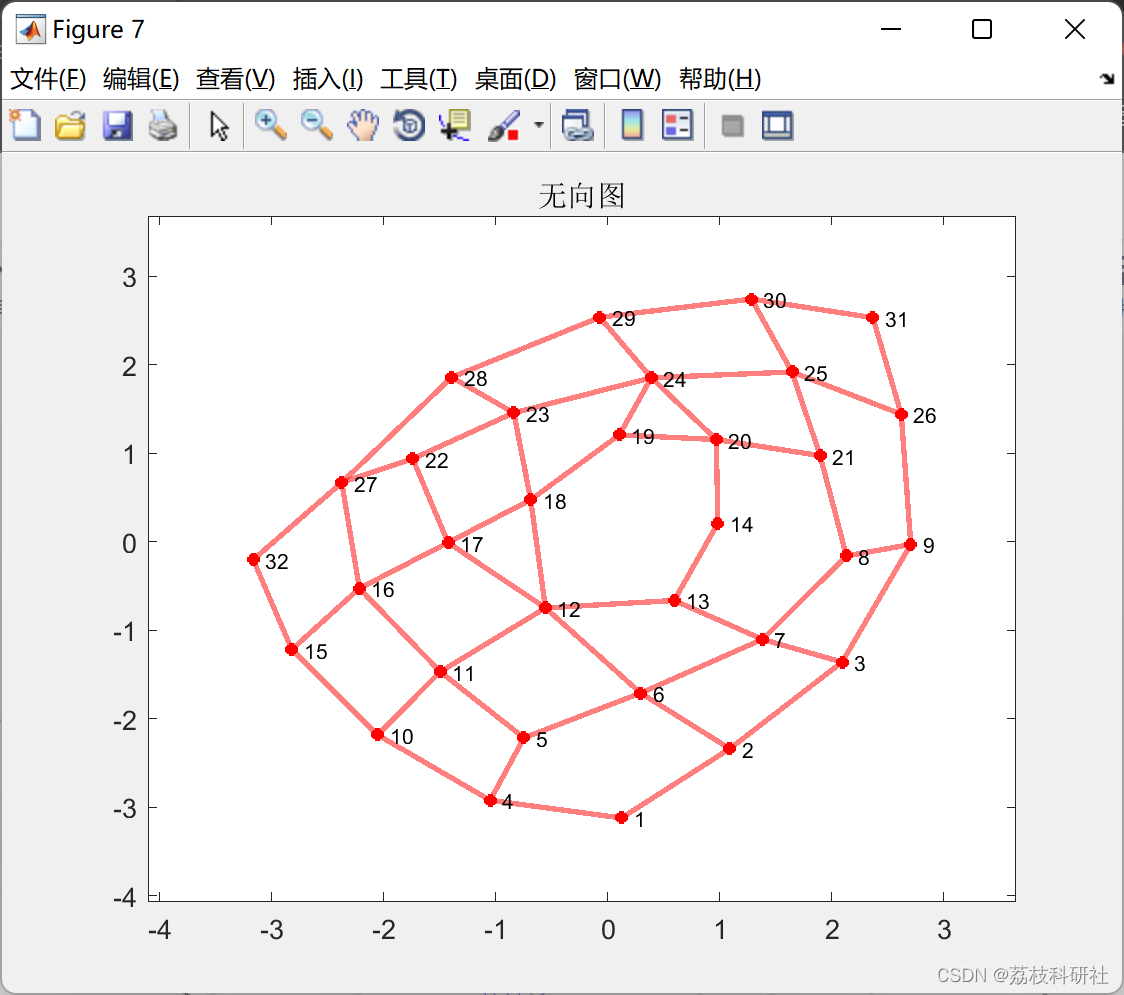
部分代码：

%% 创建汽车MC信息矩阵

Mcar=zeros(sumNcar,6); %生成Mcar=sumNcar*6阶矩阵用来储存每辆车的信息，依次为，车辆编号Mcar(:,1)、车辆种类Mcar(:,2)，1私家车，2出租车，3公交车

%1

Mcar(:,1)=1:sumNcar; %给sumNcar辆汽车依次进行编号

%2

carkind=ceil(100*rand(sumNcar,1));

for i=1:sumNcar

if carkind(i)<=Per_car(1) %carkind(i)<=25的私家车，即生成25%的私家车

carkind(i)=1;

elseif carkind(i)<=Per_car(1)+Per_car(2) %25<Per_car(1)+Per_car(2)<=70的出租车，即生成百分之45的出租车

carkind(i)=2;

else %等价于70<Per_car(1)+Per_car(2)<=100的出租车，即生成百分之30的出租车

carkind(i)=3;

end

end

Mcar(:,2)=carkind; %给sumNcar辆汽车依次进行种类编号

%34

%OD节点概率向量 ,建立OD出行概率矩阵

Pod=ones(1,32)/32; %创建一个1*32阶的全1矩阵，并将元素都除以32变成1*32阶的全00313矩阵

Pod_arry=zeros(1,10000); %创建一个1*10000阶的全1矩阵

Pod_arry(1:ceil(10000*Pod(1)))=1; %Pod(1)=0.0313 ， 10000*Pod(1)=312.5000 ，ceil(10000*Pod(1))=313 ，Pod_arry(1:ceil(10000*Pod(1)))=1相当于将Pod_arry第1-313列的元素全部换为1

for i=2:32

Pod_arry(ceil(10000*sum(Pod(1:i-1)))+1:ceil(10000*sum(Pod(1:i))))=i;

%当i=2时，Pod(1:i-1)=Pod(1:1)=0.0313，sum(Pod(1:i-1))=0.0313，ceil(10000*sum(Pod(1:i-1)))=313

%当i=2时，Pod(1:i)=Pod(1:2)=【0.0313,0.0313】，sum(Pod(1:i))=0.0625，ceil(10000*sum(Pod(1:i)))=625

%当i=2时，Pod_arry(ceil(10000*sum(Pod(1:i-1)))+1:ceil(10000*sum(Pod(1:i))))=i ， 即为Pod_arry(313+1:625)=2，相当于将Pod_arry第314-625列的元素全部换为1

%同理依次退出i=3 ,i=4 , ...... , i=32 ;

%1*10000阶的矩阵Pod_arry，其中最大的元素也就是i=32

end

Mcar(:,3)=Pod_arry(randperm(10000,sumNcar))'; %确定EV初始位置Mcar(:,3)

Mcar(:,4)=Pod_arry(randperm(10000,sumNcar))'; %确定EV目的地Mcar(:,4)

% 5678

Mcar(:,5)=6+2*rand(sumNcar,1); %初始时刻Mcar(:,5)，这个初试出发时刻不应该这么随机生成，应该参考文献服从正态分布函数公式来吧

Mcar(:,6)=18+2*rand(sumNcar,1); %返程时刻Mcar(:,6)，同理这个返程时刻，想想应该怎么办

Mcar(:,7)=200+100*rand(sumNcar,1); %ev容量，这个ev容量确定的也不合理

Mcar(:,8)=normrnd(0.3,0.1,[sumNcar,1]); %生成服从正态分布的初始soc

Mcar(:,9)=normrnd(40,1,[sumNcar,1]); %生成服从正态分布的速度，这个速度的生成是不是有点不合理

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]李晓辉,李磊,刘伟东,赵新,谢秦.基于动态交通信息的电动汽车充电负荷时空分布预测[J].电力系统保护与控制,2020,48(01):117-125.DOI:10.19783/j.cnki.pspc.181616.

[2]李磊,赵新,李晓辉,刘伟东,刘小琛,冯炜.基于动态交通信息的电动汽车充电需求预测模型及其对配网的影响分析[J].电网与清洁能源,2020,36(03):107-118.

🌈4 Matlab代码实现