二阶RC低通滤波器的仿真与计算

最新推荐文章于 2025-03-26 09:06:39 发布
最新推荐文章于 2025-03-26 09:06:39 发布
阅读量1.6k 收藏 11
点赞数 5
分类专栏： 信号链 运放电路 硬件常识 文章标签： 硬件工程 学习 嵌入式硬件
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_36853953/article/details/144012390
版权

一阶RC低通滤波器很常见，课本上有详细的公式和解释，各种资料都很多。但是两个一阶RC组成的二阶RC低通滤波器，或更多RC级联，信号链上其实很常见，参见图1，但相关的资料却不是很常见。最近在ADI新出的《电路设计常见指南》中看到了相关的公式，所以这里特别记录一下。

图片
图1 一个典型的TIA信号链（如果后级LPF截止频率与TIA一样，那么信号链的总截止频率会比第一级TIA低，所以通常后级LPF截止频率要大于TIA的至少十倍，才能符合设计目标）

一、一阶RC低通滤波器

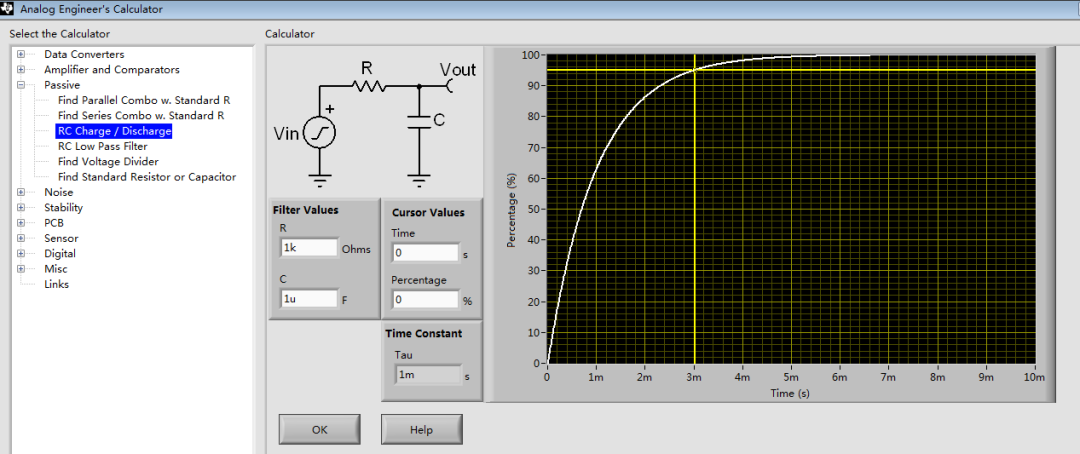
先简单复习一下的一阶RC低通滤波器。这里我们使用TI的Analog Engineer’s calculator小工具，可以快速了解它的瞬态和频域响应。 

图片
图1 一阶RC的瞬态响应（充放电时间） 

最低0.47元/天 解锁文章
二阶rc无源低通滤波器matlab,二阶rc无源低通滤波电路
weixin_29903713的博客
03-18 5735
摘要 在信号处理中，滤波的优劣直接影响信息的准确性。模拟滤波虽然快捷但不灵活，数字滤波效果虽好但复杂。所以文中提出一种以模拟滤波器为基准，设计具有相同功能而且参数可调的数字滤波器的方法。并以二阶RC无源低通滤波电路为例对此过程进行说明，与模拟滤波电路和传统的数字滤波相比，该方法不仅比传统的数字滤波算法简单快捷，而且可有效防止模拟电路中器件的寄生参数、精度、温度等的影响，使滤波更加稳定。随着信息科...
二阶无源低通滤波器幅频特性曲线_一文看懂二阶lc低通滤波器的设计及原理
weixin_39939303的博客
12-20 1万+
二阶低通滤波器的设计一、系统设计方案选择1、总方案设计方案框图2、子框图的作用RC网络的作用在电路中RC网络起着滤波的作用，滤掉不需要的信号，这样在对波形的选取上起着至关重要的作用，通常主要由电阻和电容组成。放大器的作用电路中运用了同相输入运放，其闭环增益RVF=1+R4/R3同相放大器具有输入阻抗非常高，输出阻抗很低的特点，广泛用于前置放大级。反馈网络的作用将输出信号的一部分或全部通过牧电路印象...
二阶滤波器计算工具
08-23
二阶滤波器计算设计的小工具，可以使用，计算电容值、计算频率等功能，挺全的，挺好用的
二阶滤波算法总结（对RC滤波算法整理的部分修正和完善）
qq_28149763的博客
09-24 2403
本文是之前已发博客的完善和补充。
RC电路（四）：RC低通滤波器
既有随处可栖的江湖，也有追风逐梦的骁勇！
03-26 1491
低通滤波（Low-pass Filter）是一种过滤方式，使低频信号能正常通过，信号频率高于某个频率（截止频率）时被阻隔、减弱，不能通过。
MFB二阶低通滤波器仿真图
06-15
multisim12版本的，无限增益多路反馈二阶低通有源滤波器，仿真源文件。免费共享了！
一阶RC低通滤波器——cadence virtuoso仿真
qq_57058268的博客
10-17 1万+
今天在听B站上张鸿老师讲模拟集成电路第六章——Amp频率响应的时候讲到了一阶RC网络，自己对于这一部分知识的掌握略显生疏，于是在课后进行了仿真调试，将所得结果记录在此。
二阶RC滤波器
qq_45776815的博客
10-14 2万+
二阶RC低通滤波器是一种常用的电路，用于滤除输入信号中高频部分，只保留低频部分。
设计RC低通/高通滤波器滤除混合信号中的高频/低频信号并基于Multisim进行仿真模拟实验
2302_80792487的博客
06-04 4348
通过对比上述图像中，输入信号与滤波后的输出信号，原始信号与滤波后的输出信号以及观察RC低通、高通滤波器的频率响应曲线。我们可以发现，对于RC低通滤波器而言，在截止频率为5Hz的实验前提下，二阶RC低通滤波器的过滤效果更好，性能更高，在截止频率之后信号衰减更快，信号衰减量为-10.097dB。对于RC高通滤波器而言，一阶RC高通滤波器过滤效果足够好，信号的完整性较高，其过滤效果已经可以充分满足实验需求，在截止频率为50Hz的实验前提下，信号衰减为-3.09dB。
PWM波转DC直流之二阶RC低通滤波器设计
yuyan7045的博客
10-18 2万+
1.原理 2.参数计算 3.电路仿真 4.硬件电路测试 5.参数选型的注意
二阶有源低通滤波器的设计和仿真分析(
10-21
本设计有源低通二阶滤波器(又称Sallen-Key 低通滤波器)使用公式法计算得到各参数,本设计从运算放大器的输出到同相端输入间引入一个负反馈构建而成。本文详细叙述了如何用计算法设计有源低通二阶滤波器的方法，并用仿真软件EWB进行电路仿真，得出了电路的幅频特性和相频特性，并进行了仿真分析和误差结果分析。
RC带通滤波器pspice仿真电路
05-22
简单的图，只是为了自己记录，看看以后能不能长进
二阶RC滤波试验
08-22
滤波器是一种能使有用信号顺利通过而同时对无用频率信号进行抑制（或衰减）的电子装置。工程上常用它来做信号处理、数据传送和抑制干扰等。本实验方案主要是针对由 R、C 组成的无源滤波器进行介绍，对各种无源RC 滤波器的幅频特性和相频特性进行分析。 然后对转折频率ωC =1000rad/s 的情形分别提出一个一阶RC 无源低、高通滤波器和一个二阶RC 无源低通滤波器的学生实验设计方案，对所设计的方案进行频率特性的研究
二阶电路响应的仿真
11-01
在一个动态网络中，若同时有两个性质独立的储能元件L和C存在， 则这个可以用二阶微分方程描述的动态电路称为二阶电路。
二阶有源低通滤波器
04-06
滤波器是一种能使有用频率信号通过而同时抑制无用频率信号的电子装置，常用于信号处理、数据传输和干扰抑制等方面。其中，有源低通滤波电路由集成运放和无源元件电阻和电容构成。它的功能是允许从零到某个截止频率的信号无衰减地通过，而对其他频率的信号有抑制作用，有源低通滤波电路可以用来滤除高频干扰信号。
二阶低通有源滤波器设计与仿真测试
热门推荐
weixin_44302723的博客
08-07 5万+
本文介绍了一种压控电源法二阶有源低通滤波器的设计方法、参数计算过程，并通过Multisim软件仿真了所设计的电路，其频率特性满足设计要求。
二阶RC滤波器截止频率计算
weixin_42550185的博客
05-11 9058
二阶RC滤波器截止频率计算公式为 f_c = 1 / ( 2 ∗ π ∗ √ ( R 1 ∗ R 2 ∗ C1*C2 ) ）
一阶RC低通滤波电路推演与仿真
RichardLiTian的博客
11-13 5399
数学推导RC一阶低通滤波电路的表达式方程，并且用Matlab和Modelsim对一阶低通滤波电路进行了仿真
二阶RC低通滤波器
最新发布
05-08
<think>嗯，用户现在想查找关于二阶RC低通滤波器的设计方案和相关参数计算。之前我已经回答过STM32使用PWM模拟DAC的方案，其中用到了二阶RC低通滤波器，用户可能是在那个项目的基础上需要更详细的设计方法。我需要结合之前的回答和现在提供的三个引用来给出合适的回答。 首先，用户引用的三个文献中，提到了二阶RC无源和有源滤波器的设计方法，包括参数计算、仿真以及截止频率的变化。用户的问题是如何设计二阶RC低通滤波器及计算参数，所以我需要把这些信息整合起来。 用户的上一个问题是关于PWM转DAC的方案，其中提到了二阶RC滤波器的参数，比如R1=1kΩ，R2=10kΩ，C1=100nF，C2=10nF，以及截止频率的计算公式。现在用户需要更通用的设计方案，可能需要详细的设计步骤和参数选择方法。 根据引用[1]，提到了使用Matlab和VC++设计数字滤波器的方法，但用户现在需要的是模拟电路的设计，所以可能主要参考引用[2]和[3]。引用[2]指出两阶级联后的截止频率会比一阶低，而引用[3]提到了有源滤波器的设计步骤，包括电容选择和电阻计算。 用户的问题可能涉及到无源和有源两种二阶RC滤波器的设计，但之前的回答里用的是无源滤波器，所以可能需要重点讲无源，但也可以补充有源的设计作为扩展。 接下来，我需要整理二阶RC低通滤波器的设计步骤，包括参数计算、截止频率公式、元件选择，以及可能的设计考虑因素如纹波、负载影响等。同时，结合用户提供的引用，比如级联后的截止频率变化，可能需要说明如何调整参数来达到目标频率。 另外，用户之前的方案中用了二阶无源滤波，可能需要强调无源和有源的区别，比如有源滤波器可以避免负载效应，提高性能，但需要运放，而无源更简单但受负载影响大。 在参数计算部分，需要给出截止频率的公式，并说明如何根据所需的截止频率选择R和C的值。可能需要举例说明，比如用户之前用的参数，计算截止频率是否符合。引用[2]中提到级联后的截止频率是120Hz，而单级是180Hz，这说明级联后的截止频率计算方式不同，可能需要用更准确的公式或仿真来确定。 同时，用户可能需要知道如何通过调整R和C来改变截止频率，以及如何平衡元件的值选择，比如避免使用过小或过大的电阻电容值，以免影响电路性能或实际选型的可行性。 最后，可能需要提到仿真验证的重要性，如使用Matlab或电路仿真软件来验证设计，如引用[1]和[2]中提到的仿真步骤，确保设计的正确性。用户之前的回答里提到了校准方法，可能在这里也可以建议通过仿真和实际测试来调整参数。 总结来说，回答需要包括无源和有源滤波器的设计方法，参数计算公式，元件选择步骤，设计注意事项，以及仿真和测试的建议。同时，结合用户之前的问题中的具体参数作为例子，帮助用户更好地理解。</think>以下为二阶RC低通滤波器的设计方案及参数计算详解，结合工程实践与理论分析： --- ### 一、基本拓扑结构 **典型电路形式**： 1. **无源型**： ``` 输入信号 → R1 → C1 → R2 → C2 → 输出 │ │ │ GND GND GND ``` 2. **有源型**（Sallen-Key拓扑）： ``` 输入信号 → R1 → C1 → 运放同相端 │ │ R2 C2 │ │ GND 运放输出 ``` --- ### 二、关键参数计算公式 1. **截止频率**： $$ f_c = \frac{1}{2π\sqrt{R1R2C1C2}} \quad \text{(无源型)} $$ $$ f_c = \frac{1}{2π\sqrt{R1R2C1C2}} \quad \text{(有源型，Sallen-Key)} $$[^2][^3] 2. **品质因数Q值**（仅适用于有源型）： $$ Q = \frac{1}{2}\sqrt{\frac{R1C1}{R2C2}} $$ 3. **传递函数**： $$ H(s) = \frac{1}{s^2R1R2C1C2 + s(R1C1 + R2C2 + R1C2) + 1} $$ --- ### 三、设计步骤（以无源型为例） 1. **确定设计要求**： - 截止频率$f_c$ - 输入/输出阻抗要求 - 负载特性 2. **元件参数选择原则**： - 推荐电容值范围：$1nF \leq C \leq 10μF$ - 电阻值范围：$1kΩ \leq R \leq 100kΩ$ - 保持$R1=R2=R$，$C1=C2=C$可简化计算： $$ f_c = \frac{1}{2πRC\sqrt{2}} $$ 3. **设计实例**（目标$f_c=1kHz$）： ```math 取R=10kΩ → C = \frac{1}{2π×10kΩ×1kHz×\sqrt{2}} ≈ 11.3nF → 取标称值10nF ``` **实际参数**：$R1=R2=10kΩ$，$C1=C2=10nF$ --- ### 四、工程实践要点 1. **级联特性**： - 两阶相同参数RC级联后，实际截止频率会降低至原值的$0.64$倍[^2] - 示例：单级$f_c=180Hz$ → 两级级联后$f_c≈120Hz$ 2. **负载效应补偿**： - 无源型建议后接高输入阻抗缓冲器（如运放电压跟随器） - 有源型通过运放隔离可消除负载影响 3. **参数优化建议**： - 采用E24系列标准阻值 - 优先选用NP0/C0G材质的电容 - 高频应用时需考虑PCB寄生参数 --- ### 五、仿真验证方法 1. **MATLAB频响分析**： ```matlab R = 10e3; C = 10e-9; sys = tf(1, [R^2*C^2 3*R*C 1]); bode(sys); ``` 2. **实际电路测试**： - 使用信号发生器+示波器扫频测量 - -3dB点验证：输出电压降至输入电压的70.7% --- ### 六、性能提升方案 1. **多阶级联**：四阶滤波器可达-80dB/dec衰减斜率 2. **有源优化**：通过运放调节Q值，实现Butterworth/Bessel特性 3. **温度补偿**：选用温度系数匹配的电阻电容
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值