HDU6482 A Path Plan

最新推荐文章于 2021-08-04 15:15:41 发布

原创最新推荐文章于 2021-08-04 15:15:41 发布 · 838 阅读

2 ·

CC 4.0 BY-SA版权

组合数学专栏收录该内容

6 篇文章

订阅专栏

博客围绕一个算法问题展开，给定WNJXYK和Destinys从宿舍到教室的坐标，要求计算两人路径不相交的方案数。解题思路是运用Lindström–Gessel–Viennot定理，此题为n = 2的情形。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

http://acm.hdu.edu.cn/showproblem.php?pid=6482

Problem Description
WNJXYK hates Destinys so that he does not want to meet him at any time. Luckily, their classrooms and dormitories are at different places. The only chance for them to meet each other is on their way to classrooms from dormitories.
To simple this question, we can assume that the map of school is a normal rectangular 2D net. WNJXYK’s dormitory located at (0,y1) and his classroom located at (x1,0). Destinys’s dormitory located at (0,y2) and his classroom is located at (x2,0). On their way to classrooms, they can do two kinds of movement : (x,y)->(x,y-1) and (x,y)->(x+1,y).
WNJXYK does not want to meet Destinys so that he thinks that it is not safe to let his path to classroom from dormitory has any intersect point with Destinys ‘s. And then he wonders how many different paths for WNJXYK and Destinys arriving their classrooms from dormitories safely.

题意：求 $(0, y 1) - > (x 1, 0) ， (0, y 2) - > (x 2, 0)$ 的不相交路径的方案数。
思路：
按照Lindström–Gessel–Viennot定理（维基：https://en.wikipedia.org/wiki/Lindström–Gessel–Viennot_lemma）
对于一张无边权的DAG图，给定n个起点和对应的n个终点，n条不相交路径的方案数为：

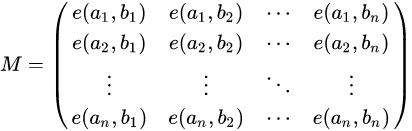
在这里插入图片描述
其中 ai 代表路径的起点 bi 代表路径的终点， e(ai,bj) 代表ai到bj的方案数。
对于这道题，就是n=2的情形。
答案是:

|  e(a1,b1)    e(a1,b2)  |
|  e(a2,b1)    e(a2,b2)  |

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007

int T,x[3],y[3];
ll fac[200000+100];

ll pow_mod(ll a,ll n)
{
    if(n==0)return 1;
    ll x=pow_mod(a,n/2);
    x=x*x%mod;
    if(n&1)x=x*a%mod;
    return x;
}

ll c(ll n,ll m)
{
    return fac[n]*pow_mod(fac[m],mod-2)%mod*pow_mod(fac[n-m],mod-2)%mod;
}

int main()
{
    cin>>T;
    fac[0]=1;
    for(int i=1;i<=200000;i++)fac[i]=fac[i-1]*i%mod;
    while(T--)
    {
        cin>>x[1]>>x[2]>>y[1]>>y[2];
        cout<<(c(x[1]+y[1],x[1])*c(x[2]+y[2],x[2])%mod-c(x[1]+y[2],x[1])*c(x[2]+y[1],x[2])%mod+mod)%mod<<endl;
    }
    return 0;
}