hdu 6482 LGV求互不相交路径条数

最新推荐文章于 2021-09-30 14:42:49 发布

余西子

最新推荐文章于 2021-09-30 14:42:49 发布

阅读量368

点赞数

CC 4.0 BY-SA版权

分类专栏：杂算法

本文链接：https://blog.youkuaiyun.com/qq_41955236/article/details/90199382

杂算法专栏收录该内容

8 篇文章

订阅专栏

本文解析了HDU 6482题目的求解思路，利用组合数学原理，通过杨辉三角关系和LGV公式计算路径条数。提供了完整的C++代码实现，包括快速幂、组合数计算等关键算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6482

题意：

给你x1,x2,y1,y2 (x1<x2,y1<y2)，问你从(0,y1)->(x1,0),(0,y2)->(0,x2),只能往右、往下走的时候的路径不相交的条数是多少。

做法：

稍微画一下就知道从(0,y1)->(x1,0),的路径条数像是杨辉三角的关系，即 $C_{y1+x1}^{y1}$ ，。

这里就要介绍一下LGV了，设 $e(a_{i},b_{i})$ 为从点 $a_{i}$ 到达点 $b_{i}$ 的方案数，那么所有 $a_{i}\rightarrow b_{i}$ 的路径条数是

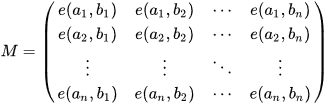
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=(int)1e9+7;
const int maxn=200005;
ll fac[maxn+5],inv_fac[maxn+5];

ll quick(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1) ans=ans*a%mod;
        a=a*a%mod;
        b/=2;
    }
    return ans;
}
void init(){
    inv_fac[0]=fac[0]=1,fac[1]=inv_fac[1]=1;
    for(int i=2;i<maxn;i++)
        fac[i]=fac[i-1]*i%mod;
    inv_fac[maxn-1]=quick(fac[maxn-1],mod-2);
    for(int i=maxn-2;i>=0;i--)
        inv_fac[i]=inv_fac[i+1]*(i+1)%mod;
}

ll C(ll n,ll m){
    if(n<0||m<0||m>n) return 0;
    if(n==m||m==0) return 1;
    return fac[n]*inv_fac[n-m]%mod*inv_fac[m]%mod;
}
ll x[2],y[2];
int main(){
    init();
    int t;
    cin>>t;
    while(t--){
        scanf("%lld%lld%lld%lld",&x[0],&x[1],&y[0],&y[1]);
        ll ans1=C(x[1]+y[1],y[1]),ans2=C(x[0]+y[1],y[1]);
        ll ans3=C(y[0]+x[1],y[0]),ans4=C(x[0]+y[0],y[0]);
        printf("%lld\n",((ans1*ans4-ans2*ans3)%mod+mod)%mod);

    }
   return 0;
}