============================================================
仿真关键时间点采样(每5秒输出一次)
============================================================
时间(s) x(m) y(m) V(m/s) α(deg) δ(deg) ny(g) n_cmd(g) r(km)
--------------------------------------------------------------------------------
0.0 0.0 1500.0 250.0 2.00 0.00 0.47 1.57 5.12
2.5 614.3 1485.1 243.2 2.66 0.66 0.56 1.62 4.54
5.0 1213.6 1443.7 237.6 2.83 0.71 0.57 1.75 3.96
7.5 1798.1 1377.5 233.2 3.04 0.76 0.59 1.98 3.39
10.0 2369.8 1288.3 229.8 3.35 0.83 0.63 2.39 2.84
12.5 2930.4 1179.2 227.2 3.88 0.97 0.72 3.18 2.30
15.0 3481.7 1056.1 224.7 4.95 1.23 0.89 4.81 1.77
17.5 4025.0 930.7 221.1 7.18 1.78 1.26 8.17 1.28
20.0 4560.2 825.3 214.7 10.08 2.47 1.66 10.59 0.89
22.5 5083.0 755.1 208.2 4.46 1.17 0.69 2.82 0.78
25.0 5593.5 686.9 203.2 9.10 2.23 1.35 9.44 0.98
27.5 6090.2 635.4 196.4 7.99 1.97 1.11 6.01 1.35
30.0 6572.6 592.0 191.4 5.81 1.44 0.76 3.64 1.77
32.5 7043.6 536.5 188.4 4.69 1.16 0.60 2.57 2.21
35.0 7506.4 458.3 187.4 4.13 1.02 0.52 2.05 2.65
37.5 7963.1 352.8 188.0 3.81 0.95 0.48 1.79 3.08
40.0 8415.8 217.9 190.2 3.57 0.89 0.46 1.63 3.52
42.5 8866.1 52.5 193.8 3.37 0.84 0.46 1.55 3.97
45.0 9315.4 -143.7 198.7 3.18 0.79 0.45 1.49 4.42
47.5 9765.1 -370.7 204.6 3.00 0.75 0.45 1.46 4.88
50.0 10216.4 -628.4 211.3 2.82 0.70 0.45 1.44 5.35
============================================================
最终状态
============================================================
仿真结束时间: 50.00 s
最终位置: x = 10217.7 m, y = -629.2 m
最终速度: V = 211.3 m/s
最终攻角: α = 2.82 °
最终舵偏: δ = 0.70 °
最终实际过载: ny = 0.45 g
最终指令过载: n^c = 1.44 g
最终脱靶量: 5354.8 m (5.35 km)
最终质量: m = 667.0 kg
最终动压: q = 23445.5 Pa
============================================================
全程统计量
============================================================
攻角 α 最大: 10.11 ° 最小: 1.94 ° 平均: 4.72 °
舵偏 δ 最大: 2.47 ° 最小: 0.00 ° 平均: 1.17 °
实际过载 ny 最大: 1.66 g 最小: 0.42 g 平均: 0.74 g
指令过载 n^c 最大: 10.92 g 最小: 0.01 g 平均: 3.54 g
# -*- coding: utf-8 -*-
"""
优化版3:导弹纵向三自由度 + 比例导引 + 姿态控制环
- 已解决中文乱码(使用中文字体)
- 增大控制增益,让导弹能产生明显机动
- 调整过载方向与计算方式
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
import os
# === 解决中文乱码 ===
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'Arial Unicode MS'] # 优先使用 SimHei
plt.rcParams['axes.unicode_minus'] = False # 负号显示正常
# ============================= 常数 =============================
g = 9.8
rho = 1.05
S = 0.12
Jz = 930.0
m0 = 673.0
mdot = -0.12
P = 265.0
Cx0 = 0.4
Cx_a = 0.0778
Cy_a = 0.3916
mz_a = -0.0934
mz0 = -0.0036
Cy_de = -0.08 # 反转符号 + 略增大
mz_de = 0.38 # 反转符号 + 增大恢复力矩
b_A = 1.2
# 控制参数(大幅提高增益,让导弹能转弯)
N = 4.5 # 比例导引常数
Kp_n = 0.35 # 过载比例增益(增大)
Kd_n = 18.0 # 角速度阻尼(增大)
tau_e = 0.10 # 舵面动态时间常数
delta_max = 30.0 # 最大舵偏角度 °
delta_rate_max = 250.0 # 最大舵偏速率 °/s
# 初始状态
x0 = 0.0
y0 = 1500.0
V0 = 250.0
theta0 = 0.0 * np.pi/180
vartheta0 = 2.0 * np.pi/180 # 初始小扰动
omega0 = 0.0
delta0 = 0.0
integ0 = 0.0
xm = 4900.0
ym = 0.0
t_span = (0, 50)
max_step = 0.004
OUTPUT_DIR = "missile_optimized_results"
os.makedirs(OUTPUT_DIR, exist_ok=True)
# ============================= 动力学 =============================
def dynamics(t, state):
x, y, V, theta, vartheta, omega, delta_e, integ_n = state
V = max(V, 10.0)
m = max(m0 + mdot * t, 120.0)
q = 0.5 * rho * V**2
alpha = vartheta - theta
alpha_deg = np.degrees(alpha)
Cx = Cx0 + Cx_a * abs(alpha_deg)
Cy = Cy_a * alpha_deg + Cy_de * np.degrees(delta_e)
mz = mz_a * alpha_deg + mz0 + mz_de * np.degrees(delta_e)
X = q * S * Cx
Y = q * S * Cy
Mz = q * S * b_A * mz
# 加速度(切向 & 法向)
a_tang = (P * np.cos(alpha) - X - m * g * np.sin(theta)) / m
a_norm = (P * np.sin(alpha) + Y - m * g * np.cos(theta)) / m
dV_dt = a_tang
dtheta_dt = a_norm / V
domega_dt = Mz / Jz
dvartheta_dt = omega
dx_dt = V * np.cos(theta)
dy_dt = V * np.sin(theta)
# 比例导引
xr, yr = xm - x, ym - y
r = np.sqrt(xr**2 + yr**2 + 1e-10)
Vr = np.array([-V * np.cos(theta), -V * np.sin(theta)])
los_rate = np.cross([xr, yr], Vr) / r**2
r_dot = np.dot([xr, yr], Vr) / r
n_cmd = N * abs(r_dot) * abs(los_rate) / g
n_cmd = np.clip(n_cmd, -20, 30)
# 当前过载(更直接用力计算)
ny_meas = (Y + P * np.sin(alpha)) / (m * g)
# 控制律
e_n = n_cmd - ny_meas
delta_cmd = Kp_n * e_n - Kd_n * omega # 注意:这里未加负号,根据 mz_de 符号已调整
delta_cmd = np.clip(delta_cmd, -delta_max, delta_max) * np.pi / 180
ddelta_dt = (delta_cmd - delta_e) / tau_e
ddelta_dt = np.clip(ddelta_dt, -delta_rate_max*np.pi/180, delta_rate_max*np.pi/180)
d_integ_dt = e_n * 0.1 # 弱积分,防止累积过大
dstate = [dx_dt, dy_dt, dV_dt, dtheta_dt, dvartheta_dt, domega_dt, ddelta_dt, d_integ_dt]
aux = {
'alpha_deg': alpha_deg,
'ny': ny_meas,
'n_cmd': n_cmd,
'delta_deg': np.degrees(delta_e),
'r': r,
'm': m
}
return dstate, aux
def main():
state0 = [x0, y0, V0, theta0, vartheta0, omega0, delta0, integ0]
sol = solve_ivp(
lambda t, y: dynamics(t, y)[0],
t_span, state0,
method='RK45',
max_step=max_step,
rtol=1e-6, atol=1e-8
)
if not sol.success:
print("求解失败:", sol.message)
return
t = sol.t
states = sol.y.T
auxs = [dynamics(ti, yi)[1] for ti, yi in zip(t, states)]
results = {k: np.array([a[k] for a in auxs]) for k in auxs[0]}
# 绘图
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
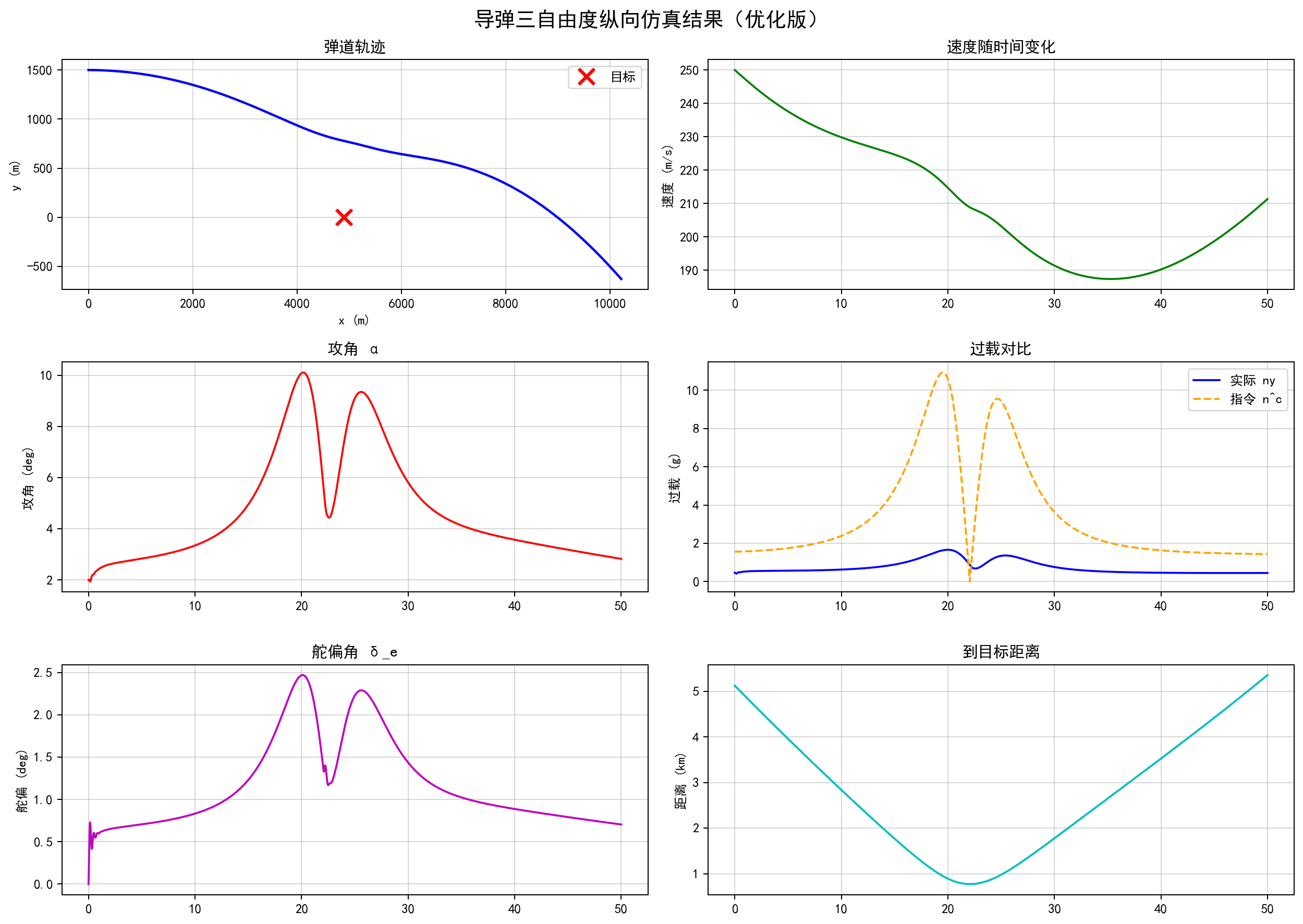
fig.suptitle('导弹三自由度纵向仿真结果(优化版)', fontsize=16)
# 轨迹
axes[0,0].plot(states[:,0], states[:,1], 'b-', lw=1.8)
axes[0,0].plot(xm, ym, 'rx', ms=12, mew=2.5, label='目标')
axes[0,0].grid(True, alpha=0.5)
axes[0,0].set_xlabel('x (m)')
axes[0,0].set_ylabel('y (m)')
axes[0,0].set_title('弹道轨迹')
axes[0,0].legend(loc='upper right')
# 速度
axes[0,1].plot(t, states[:,2], 'g-')
axes[0,1].grid(True, alpha=0.5)
axes[0,1].set_ylabel('速度 (m/s)')
axes[0,1].set_title('速度随时间变化')
# 攻角
axes[1,0].plot(t, results['alpha_deg'], 'r-')
axes[1,0].grid(True, alpha=0.5)
axes[1,0].set_ylabel('攻角 (deg)')
axes[1,0].set_title('攻角 α')
# 过载
axes[1,1].plot(t, results['ny'], 'b-', label='实际 ny')
axes[1,1].plot(t, results['n_cmd'], 'orange', ls='--', label='指令 n^c')
axes[1,1].grid(True, alpha=0.5)
axes[1,1].legend()
axes[1,1].set_ylabel('过载 (g)')
axes[1,1].set_title('过载对比')
# 舵偏
axes[2,0].plot(t, results['delta_deg'], 'm-')
axes[2,0].grid(True, alpha=0.5)
axes[2,0].set_ylabel('舵偏 (deg)')
axes[2,0].set_title('舵偏角 δ_e')
# 距离
axes[2,1].plot(t, results['r']/1000, 'c-')
axes[2,1].grid(True, alpha=0.5)
axes[2,1].set_ylabel('距离 (km)')
axes[2,1].set_title('到目标距离')
plt.tight_layout()
filename = f"missile_opt3_t{int(t[-1])}s_miss{int(results['r'][-1])}m.png"
savepath = os.path.join(OUTPUT_DIR, filename)
plt.savefig(savepath, dpi=180, bbox_inches='tight')
plt.close()
print(f"仿真完成")
print(f"最终位置: x = {states[-1,0]:.1f} m, y = {states[-1,1]:.1f} m")
print(f"最终脱靶量: {results['r'][-1]:.1f} m")
print(f"图片已保存: {savepath}")
if __name__ == "__main__":
main()






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








