本文为专著《实时数字信号处理——基于TMS320c6x_DSK平台的Matlab到C》的学习笔记，引用了书中的部分内容，若有侵权，请联系本人删除
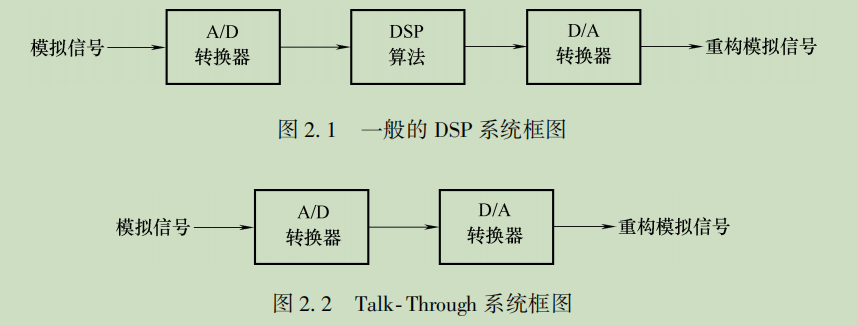
采样与重构
当我们获得现实世界中的信号以后
，
为了以数字化的形式处理它
，
我们首先将 它从模拟形式转换为更易处理的数字形式。
其中包括抓取
，
或者称为采样
（ sampling）， 即信号在一些特定时间的值。
为了防止混叠
，
模数转换器
（ADC）
的采样频率
F
s
必须大于等于输入模拟信号最大频率 f
h
的两倍。
许多
DSP
系统转移数据时也是以块为单位
，
称作一帧
（ frame） 。
直入直出流程操作 （Talk- Through）
滤波——FIR 数字滤波器 Finite Impulse Response
是最为普通的数字信号处理操作
。
滤波器能够用来抑制噪声
、
增强信号
、 移除或衰减某一特定频率，
或者执行某一专门的操作
，
比如微分
、 积分或者希尔伯 特变换。
都是离散时间滤波器
（
连续时间
FIR
滤波器是不存在的）
FIR 数字滤波器的Python实现
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
FIR数字滤波器设计、应用与可视化
本脚本演示如何设计FIR滤波器，将其应用于含噪声的信号，并通过多种可视化方式
对比滤波前后的效果，以及展示滤波器的频率特性。
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.fft import fft, fftfreq, fftshift
import os
from datetime import datetime
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS'] # 优先使用黑体或Arial Unicode MS
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
def generate_test_signal(fs, duration, freq_components, noise_level=0.5):
"""
生成测试信号，包含多个正弦波分量和高斯噪声
参数:
fs -- 采样频率 (Hz)
duration -- 信号持续时间 (秒)
freq_components -- 频率分量列表，格式为[(频率, 幅度, 相位), ...]
noise_level -- 噪声强度
返回:
t -- 时间向量
signal_clean -- 无噪声的原始信号
signal_noisy -- 含噪声的信号
"""
t = np.linspace(0, duration, int(fs * duration), endpoint=False)
# 生成干净信号
signal_clean = np.zeros_like(t)
for freq, amplitude, phase in freq_components:
signal_clean += amplitude * np.sin(2 * np.pi * freq * t + phase)
# 添加高斯噪声
noise = noise_level * np.random.normal(size=len(t))
signal_noisy = signal_clean + noise
return t, signal_clean, signal_noisy
def design_fir_filter(fs, filter_type='lowpass', cutoff_freq=None, numtaps=101,
window='hamming', plot_response=True, save_dir='figures'):
"""
设计FIR滤波器
参数:
fs -- 采样频率 (Hz)
filter_type -- 滤波器类型: 'lowpass', 'highpass', 'bandpass', 'bandstop'
cutoff_freq -- 截止频率，根据滤波器类型有不同的格式:
- 低通/高通: 单个数值
- 带通/带阻: 元组 (low_freq, high_freq)
numtaps -- 滤波器阶数(抽头数)
window -- 窗函数类型
plot_response -- 是否绘制滤波器频率响应
save_dir -- 保存图像的目录
返回:
fir_coefficients -- FIR滤波器系数
"""
nyquist = fs / 2.0 # 奈奎斯特频率
# 根据滤波器类型标准化截止频率
if filter_type == 'lowpass':
if cutoff_freq is None:
cutoff_freq = 0.2 * nyquist
normalized_cutoff = cutoff_freq / nyquist
fir_coefficients = signal.firwin(numtaps, normalized_cutoff, window=window)
elif filter_type == 'highpass':
if cutoff_freq is None:
cutoff_freq = 0.3 * nyquist
normalized_cutoff = cutoff_freq / nyquist
fir_coefficients = signal.firwin(numtaps, normalized_cutoff, window=window, pass_zero=False)
elif filter_type == 'bandpass':
if cutoff_freq is None:
cutoff_freq = (0.1 * nyquist, 0.4 * nyquist)
low_freq, high_freq = cutoff_freq
normalized_low = low_freq / nyquist
normalized_high = high_freq / nyquist
fir_coefficients = signal.firwin(numtaps, [normalized_low, normalized_high],
pass_zero=False, window=window)
elif filter_type == 'bandstop':
if cutoff_freq is None:
cutoff_freq = (0.2 * nyquist, 0.3 * nyquist)
low_freq, high_freq = cutoff_freq
normalized_low = low_freq / nyquist
normalized_high = high_freq / nyquist
fir_coefficients = signal.firwin(numtaps, [normalized_low, normalized_high],
pass_zero=True, window=window)
else:
raise ValueError("不支持的滤波器类型。请选择 'lowpass', 'highpass', 'bandpass' 或 'bandstop'")
# 绘制滤波器频率响应
if plot_response:
# 计算频率响应
w, h = signal.freqz(fir_coefficients, worN=8000)
freq = w * nyquist / np.pi
# 创建图形
plt.figure(figsize=(12, 8))
# 幅度响应 (线性刻度)
plt.subplot(2, 2, 1)
plt.plot(freq, np.abs(h), 'b')
plt.title(f'{filter_type} FIR 滤波器 - 幅度响应 (线性刻度)')
plt.xlabel('频率 (Hz)')
plt.ylabel('增益')
plt.grid(True)
plt.xlim(0, nyquist)
# 幅度响应 (dB刻度)
plt.subplot(2, 2, 2)
plt.plot(freq, 20 * np.log10(np.abs(h)), 'b')
plt.title(f'{filter_type} FIR 滤波器 - 幅度响应 (dB刻度)')
plt.xlabel('频率 (Hz)')
plt.ylabel('增益 (dB)')
plt.grid(True)
plt.xlim(0, nyquist)
# 相位响应
plt.subplot(2, 2, 3)
angles = np.unwrap(np.angle(h))
plt.plot(freq, angles, 'g')
plt.title(f'{filter_type} FIR 滤波器 - 相位响应')
plt.xlabel('频率 (Hz)')
plt.ylabel('相位 (弧度)')
plt.grid(True)
plt.xlim(0, nyquist)
# 脉冲响应
# 脉冲响应
plt.subplot(2, 2, 4)
plt.stem(range(len(fir_coefficients)), fir_coefficients, markerfmt='o', basefmt=" ")
plt.title(f'{filter_type} FIR 滤波器 - 脉冲响应 (系数)')
plt.xlabel('抽头索引')
plt.ylabel('系数值')
plt.grid(True)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'fir_{filter_type}_response.png'), dpi=300, bbox_inches='tight')
plt.close()
# 绘制零极点图
z, p, k = signal.tf2zpk(fir_coefficients, [1])
plt.figure(figsize=(8, 8))
plt.scatter(np.real(z), np.imag(z), s=50, c='b', marker='o', label='零点')
plt.scatter(np.real(p), np.imag(p), s=50, c='r', marker='x', label='极点')
plt.title(f'{filter_type} FIR 滤波器 - 零极点图')
plt.xlabel('实部')
plt.ylabel('虚部')
plt.grid(True)
plt.axis('equal')
circle = plt.Circle((0, 0), 1, color='k', fill=False, linestyle='--')
plt.gca().add_patch(circle)
plt.legend()
plt.savefig(os.path.join(save_dir, f'fir_{filter_type}_zeros_poles.png'), dpi=300, bbox_inches='tight')
plt.close()
return fir_coefficients
def apply_fir_filter(signal_data, fir_coefficients, use_lfilter=True):
"""
应用FIR滤波器到信号
参数:
signal_data -- 输入信号
fir_coefficients -- FIR滤波器系数
use_lfilter -- 是否使用lfilter (True) 或 filtfilt (False)
lfilter有相位延迟，filtfilt是零相位滤波
返回:
filtered_signal -- 滤波后的信号
"""
if use_lfilter:
# 使用lfilter，有相位延迟
filtered_signal = signal.lfilter(fir_coefficients, 1.0, signal_data)
else:
# 使用filtfilt，无相位延迟（零相位滤波）
filtered_signal = signal.filtfilt(fir_coefficients, 1.0, signal_data)
return filtered_signal
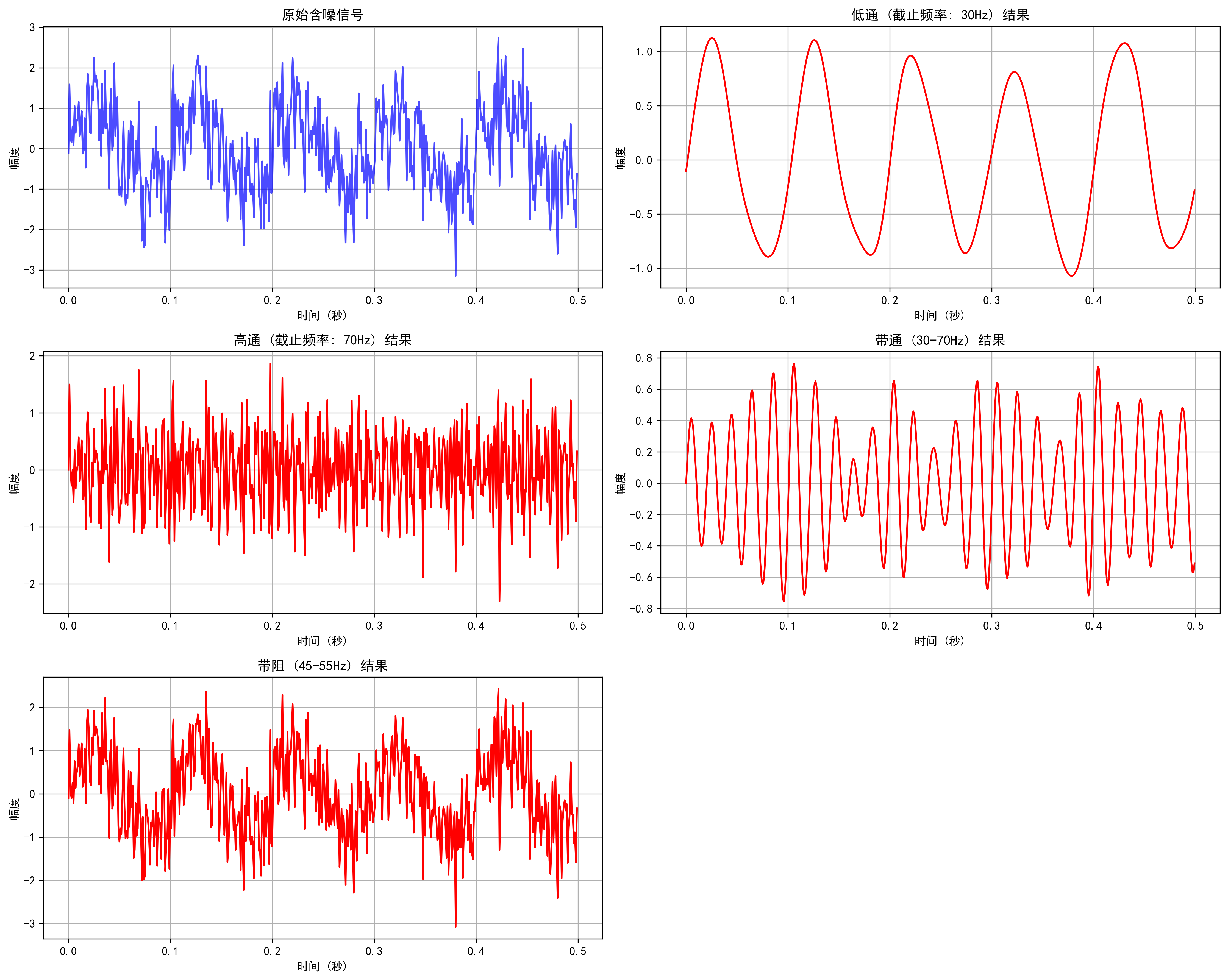
def plot_signal_comparison(t, original_signal, filtered_signal, fs, title_suffix='',
save_dir='figures', filename_suffix=''):
"""
绘制原始信号和滤波信号的对比
参数:
t -- 时间向量
original_signal -- 原始信号
filtered_signal -- 滤波后的信号
fs -- 采样频率
title_suffix -- 图标题后缀
save_dir -- 保存目录
filename_suffix -- 保存文件名后缀
"""
# 创建时域对比图
plt.figure(figsize=(14, 10))
# 时域波形
plt.subplot(2, 1, 1)
plt.plot(t, original_signal, 'b-', alpha=0.7, label='原始信号')
plt.plot(t, filtered_signal, 'r-', linewidth=2, label='滤波后信号')
plt.title(f'时域波形对比 {title_suffix}')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 计算频谱
n = len(original_signal)
dt = 1.0 / fs
# 原始信号频谱
yf_original = fft(original_signal)
xf = fftfreq(n, dt)[:n//2]
# 滤波信号频谱
yf_filtered = fft(filtered_signal)
# 频域幅值
plt.subplot(2, 1, 2)
plt.plot(xf, 2.0/n * np.abs(yf_original[:n//2]), 'b-', alpha=0.7, label='原始信号频谱')
plt.plot(xf, 2.0/n * np.abs(yf_filtered[:n//2]), 'r-', linewidth=2, label='滤波后信号频谱')
plt.title(f'频域频谱对比 {title_suffix}')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.xlim(0, fs/2)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'signal_comparison_{filename_suffix}.png'), dpi=300, bbox_inches='tight')
plt.close()
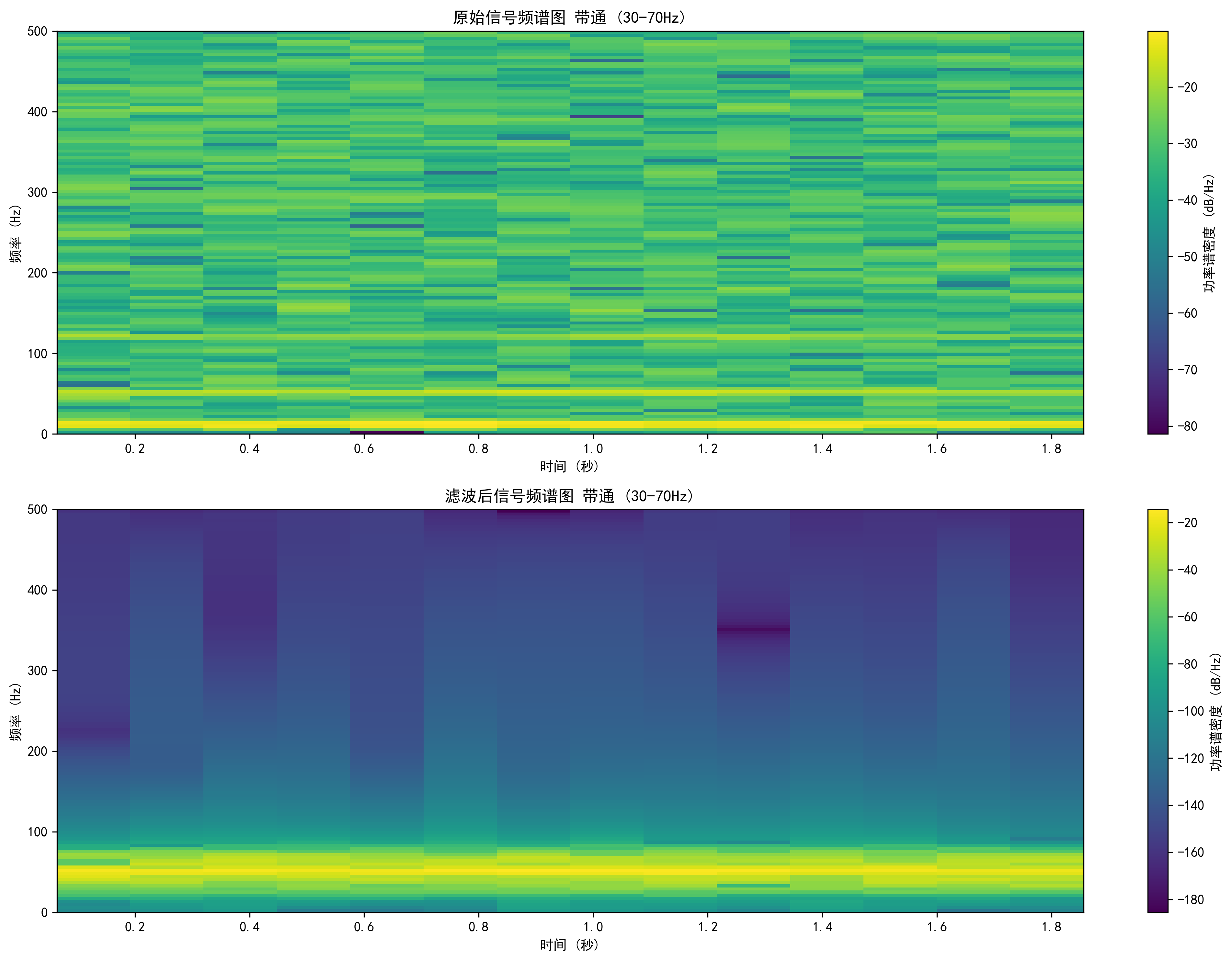
def plot_spectrogram_comparison(t, original_signal, filtered_signal, fs, title_suffix='',
save_dir='figures', filename_suffix=''):
"""
绘制原始信号和滤波信号的频谱图对比
参数:
t -- 时间向量
original_signal -- 原始信号
filtered_signal -- 滤波后的信号
fs -- 采样频率
title_suffix -- 图标题后缀
save_dir -- 保存目录
filename_suffix -- 保存文件名后缀
"""
plt.figure(figsize=(14, 10))
# 原始信号频谱图
plt.subplot(2, 1, 1)
plt.specgram(original_signal, Fs=fs, NFFT=256, noverlap=128, cmap='viridis')
plt.title(f'原始信号频谱图 {title_suffix}')
plt.xlabel('时间 (秒)')
plt.ylabel('频率 (Hz)')
plt.colorbar(label='功率谱密度 (dB/Hz)')
# 滤波信号频谱图
plt.subplot(2, 1, 2)
plt.specgram(filtered_signal, Fs=fs, NFFT=256, noverlap=128, cmap='viridis')
plt.title(f'滤波后信号频谱图 {title_suffix}')
plt.xlabel('时间 (秒)')
plt.ylabel('频率 (Hz)')
plt.colorbar(label='功率谱密度 (dB/Hz)')
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'spectrogram_comparison_{filename_suffix}.png'), dpi=300, bbox_inches='tight')
plt.close()
def analyze_filter_performance(original_clean, original_noisy, filtered_signal, fs,
filter_type, save_dir='figures'):
"""
分析滤波器性能，计算信噪比等指标
参数:
original_clean -- 原始干净信号
original_noisy -- 原始含噪信号
filtered_signal -- 滤波后的信号
fs -- 采样频率
filter_type -- 滤波器类型
save_dir -- 保存目录
"""
# 计算信噪比
def calculate_snr(signal_clean, signal_noisy):
noise = signal_noisy - signal_clean
snr = 10 * np.log10(np.sum(signal_clean**2) / np.sum(noise**2))
return snr
# 原始含噪信号的SNR
original_snr = calculate_snr(original_clean, original_noisy)
# 滤波后信号的SNR
filtered_snr = calculate_snr(original_clean, filtered_signal)
# 计算改进的SNR
snr_improvement = filtered_snr - original_snr
# 创建性能分析图
plt.figure(figsize=(12, 8))
# 信号对比
time_points = np.linspace(0, len(original_clean)/fs, 1000)
plt.subplot(3, 1, 1)
plt.plot(time_points[:100], original_clean[:100], 'g-', label='原始干净信号')
plt.plot(time_points[:100], original_noisy[:100], 'b-', alpha=0.7, label='原始含噪信号')
plt.plot(time_points[:100], filtered_signal[:100], 'r-', linewidth=2, label='滤波后信号')
plt.title(f'信号对比 (前100个样本) - {filter_type}滤波器')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 误差分析
plt.subplot(3, 1, 2)
error_before = original_noisy - original_clean
error_after = filtered_signal - original_clean
plt.plot(time_points[:200], error_before[:200], 'b-', alpha=0.7, label=f'滤波前误差 (SNR={original_snr:.2f} dB)')
plt.plot(time_points[:200], error_after[:200], 'r-', linewidth=2, label=f'滤波后误差 (SNR={filtered_snr:.2f} dB)')
plt.title(f'误差分析 - SNR提升: {snr_improvement:.2f} dB')
plt.ylabel('误差幅度')
plt.legend()
plt.grid(True)
# 计算频谱误差
n = len(original_clean)
dt = 1.0 / fs
xf = fftfreq(n, dt)[:n//2]
yf_clean = fft(original_clean)
yf_noisy = fft(original_noisy)
yf_filtered = fft(filtered_signal)
# 频谱幅值
mag_clean = 2.0/n * np.abs(yf_clean[:n//2])
mag_noisy = 2.0/n * np.abs(yf_noisy[:n//2])
mag_filtered = 2.0/n * np.abs(yf_filtered[:n//2])
plt.subplot(3, 1, 3)
plt.plot(xf, mag_noisy, 'b-', alpha=0.5, label='含噪信号频谱')
plt.plot(xf, mag_filtered, 'r-', linewidth=1.5, label='滤波后频谱')
plt.plot(xf, mag_clean, 'g--', linewidth=2, label='原始干净频谱')
plt.title('频谱对比')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.xlim(0, 100) # 限制x轴，以便更清楚地看到低频部分
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'filter_performance_{filter_type}.png'), dpi=300, bbox_inches='tight')
plt.close()
# 保存性能指标
with open(os.path.join(save_dir, 'filter_performance_metrics.txt'), 'a') as f:
f.write(f"{datetime.now().strftime('%Y-%m-%d %H:%M:%S')} - {filter_type}滤波器性能指标:\n")
f.write(f" 原始信号SNR: {original_snr:.2f} dB\n")
f.write(f" 滤波后信号SNR: {filtered_snr:.2f} dB\n")
f.write(f" SNR提升: {snr_improvement:.2f} dB\n")
f.write("-" * 50 + "\n")
print(f"{filter_type}滤波器性能分析完成。原始SNR: {original_snr:.2f} dB, 滤波后SNR: {filtered_snr:.2f} dB, 提升: {snr_improvement:.2f} dB")
def main():
"""主函数，执行FIR滤波器设计和信号处理流程"""
# 创建保存图像的目录
save_dir = 'fir_filter_results'
os.makedirs(save_dir, exist_ok=True)
# 1. 设置参数
fs = 1000 # 采样频率 (Hz)
duration = 2.0 # 信号持续时间 (秒)
# 2. 生成测试信号
# 频率分量: (频率, 幅度, 相位)
freq_components = [
(10, 1.0, 0), # 10Hz, 幅度1.0
(50, 0.5, 0), # 50Hz, 幅度0.5
(120, 0.3, 0) # 120Hz, 幅度0.3
]
noise_level = 0.7 # 噪声强度
print("生成测试信号...")
t, signal_clean, signal_noisy = generate_test_signal(fs, duration, freq_components, noise_level)
# 3. 保存原始信号图像
plt.figure(figsize=(14, 6))
plt.plot(t[:500], signal_clean[:500], 'g-', linewidth=2, label='原始干净信号')
plt.plot(t[:500], signal_noisy[:500], 'b-', alpha=0.7, label='含噪声信号')
plt.title('原始信号对比 (前500个样本)')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.savefig(os.path.join(save_dir, 'original_signals.png'), dpi=300, bbox_inches='tight')
plt.close()
# 4. 设计和应用多种FIR滤波器
filter_types = [
('lowpass', 30, '低通 (截止频率: 30Hz)'),
('highpass', 70, '高通 (截止频率: 70Hz)'),
('bandpass', (30, 70), '带通 (30-70Hz)'),
('bandstop', (45, 55), '带阻 (45-55Hz)')
]
# 为每种滤波器类型设计和应用滤波器
for filter_type, cutoff, title in filter_types:
print(f"\n设计和应用{title}...")
# 设计FIR滤波器
fir_coefficients = design_fir_filter(
fs=fs,
filter_type=filter_type,
cutoff_freq=cutoff,
numtaps=101,
window='hamming',
plot_response=True,
save_dir=save_dir
)
# 应用滤波器
filtered_signal = apply_fir_filter(signal_noisy, fir_coefficients, use_lfilter=False)
# 保存滤波后的信号 (添加这行)
np.savetxt(os.path.join(save_dir, f'filtered_signal_{filter_type}.txt'), filtered_signal, delimiter=',')
# 保存滤波器系数
np.savetxt(os.path.join(save_dir, f'fir_{filter_type}_coefficients.txt'), fir_coefficients)
# 绘制信号对比
plot_signal_comparison(
t=t,
original_signal=signal_noisy,
filtered_signal=filtered_signal,
fs=fs,
title_suffix=title,
save_dir=save_dir,
filename_suffix=filter_type
)
# 绘制频谱图对比
plot_spectrogram_comparison(
t=t,
original_signal=signal_noisy,
filtered_signal=filtered_signal,
fs=fs,
title_suffix=title,
save_dir=save_dir,
filename_suffix=filter_type
)
# 分析滤波器性能
analyze_filter_performance(
original_clean=signal_clean,
original_noisy=signal_noisy,
filtered_signal=filtered_signal,
fs=fs,
filter_type=filter_type,
save_dir=save_dir
)
# 5. 生成综合报告
print("\n生成综合报告...")
plt.figure(figsize=(15, 12))
# 画出所有滤波结果的对比
filter_results = {}
for filter_type, _, _ in filter_types:
filtered_signal_data = np.loadtxt(os.path.join(save_dir, f'filtered_signal_{filter_type}.txt'), delimiter=',')
filtered_signal = filtered_signal_data[:500] if len(filtered_signal_data) > 500 else filtered_signal_data
filter_results[filter_type] = filtered_signal
# 创建子图
plt.subplot(3, 2, 1)
plt.plot(t[:500], signal_noisy[:500], 'b-', alpha=0.7)
plt.title('原始含噪信号')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.grid(True)
positions = [(3,2,2), (3,2,3), (3,2,4), (3,2,5), (3,2,6)]
for i, (filter_type, cutoff, title) in enumerate(filter_types):
row, col, pos = positions[i]
plt.subplot(row, col, pos)
plt.plot(t[:500], filter_results[filter_type][:500], 'r-')
plt.title(f'{title} 结果')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.grid(True)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'all_filters_comparison.png'), dpi=300, bbox_inches='tight')
plt.close()
print("\nFIR滤波器设计、应用与分析完成！")
print(f"所有结果已保存到目录: {save_dir}")
print("生成的文件包括:")
print("- 滤波器频率响应图和零极点图")
print("- 时域和频域信号对比图")
print("- 频谱图对比")
print("- 滤波器性能分析图")
print("- 滤波器系数文件")
print("- 性能指标文本文件")
if __name__ == "__main__":
main()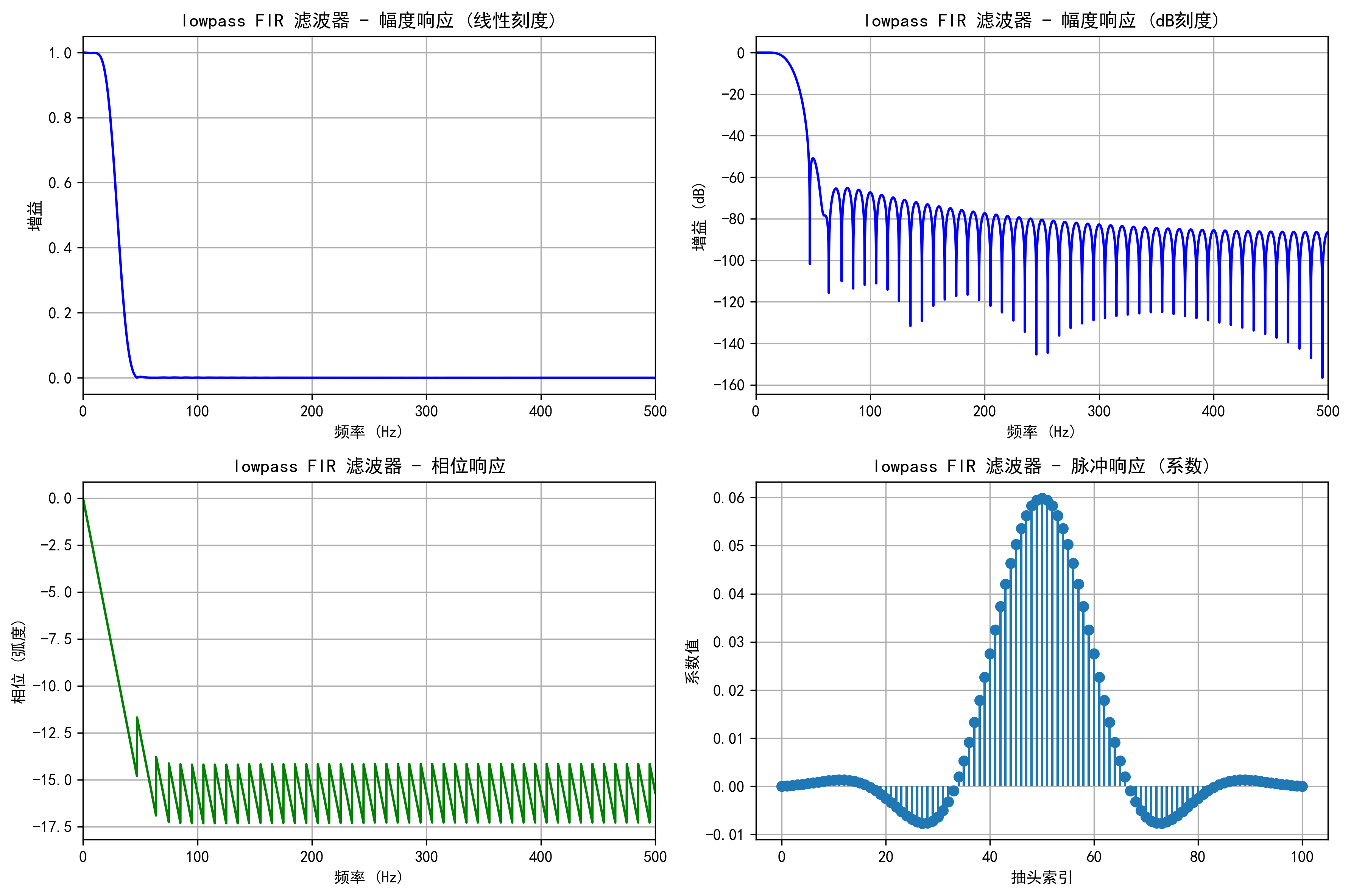
滑动平均 （Moving Average， MA） 滤波器， 并且是一种低通 FIR 滤波器
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
滑动平均（MA）滤波器设计与可视化
本脚本专门用于设计和分析滑动平均滤波器，这是一种特殊的低通FIR滤波器。
脚本会生成不同阶数的MA滤波器频率响应，并绘制出类似参考图的效果。
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.fft import fft, fftfreq
import os
from datetime import datetime
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS'] # 优先使用黑体或Arial Unicode MS
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
def design_moving_average_filter(N):
"""
设计滑动平均滤波器
参数:
N -- 滤波器阶数（抽头数）
返回:
fir_coefficients -- FIR滤波器系数（均为1/N）
"""
# 滑动平均滤波器的系数是所有值都为1/N的向量
fir_coefficients = np.ones(N) / N
return fir_coefficients
def compute_frequency_response(fir_coefficients, fs=48000):
"""
计算FIR滤波器的频率响应
参数:
fir_coefficients -- FIR滤波器系数
fs -- 采样频率 (Hz)
返回:
freq -- 频率向量
mag_db -- 幅度响应（dB）
"""
# 计算频率响应
w, h = signal.freqz(fir_coefficients, worN=8000)
freq = w * fs / (2 * np.pi) # 转换为实际频率
# 将幅度转换为dB
mag_db = 20 * np.log10(np.abs(h))
return freq, mag_db
def generate_test_signal(fs, duration, freq_components, noise_level=0.5):
"""
生成测试信号，包含多个正弦波分量和高斯噪声
参数:
fs -- 采样频率 (Hz)
duration -- 信号持续时间 (秒)
freq_components -- 频率分量列表，格式为[(频率, 幅度, 相位), ...]
noise_level -- 噪声强度
返回:
t -- 时间向量
signal_clean -- 无噪声的原始信号
signal_noisy -- 含噪声的信号
"""
t = np.linspace(0, duration, int(fs * duration), endpoint=False)
# 生成干净信号
signal_clean = np.zeros_like(t)
for freq, amplitude, phase in freq_components:
signal_clean += amplitude * np.sin(2 * np.pi * freq * t + phase)
# 添加高斯噪声
noise = noise_level * np.random.normal(size=len(t))
signal_noisy = signal_clean + noise
return t, signal_clean, signal_noisy
def apply_ma_filter(signal_data, N):
"""
应用滑动平均滤波器到信号
参数:
signal_data -- 输入信号
N -- 滑动平均窗口大小
返回:
filtered_signal -- 滤波后的信号
"""
# 创建滑动平均滤波器系数
ma_coefficients = np.ones(N) / N
# 使用lfilter应用滤波器
filtered_signal = signal.lfilter(ma_coefficients, 1.0, signal_data)
return filtered_signal
def plot_frequency_response_comparison(n_values, fs=48000, save_dir='ma_filter_results'):
"""
绘制不同阶数MA滤波器的频率响应对比图
参数:
n_values -- 不同的阶数列表
fs -- 采样频率 (Hz)
save_dir -- 保存图像的目录
"""
# 创建保存目录
os.makedirs(save_dir, exist_ok=True)
# 创建图形
plt.figure(figsize=(12, 8))
# 对于每个阶数，计算并绘制频率响应
for N in n_values:
# 设计MA滤波器
ma_coefficients = design_moving_average_filter(N)
# 计算频率响应
freq, mag_db = compute_frequency_response(ma_coefficients, fs)
# 绘制频率响应
if N == 3:
line_style = '-'
label = f'N={N}'
elif N == 7:
line_style = ':'
label = f'N={N}'
elif N == 15:
line_style = '--'
label = f'N={N}'
else: # N == 31
line_style = '-.'
label = f'N={N}'
plt.plot(freq, mag_db, line_style, linewidth=2, label=label)
# 设置图形属性
plt.title('滑动平均滤波器的频率响应曲线')
plt.xlabel('频率 (kHz)')
plt.ylabel('|H(e^jω)|/dB')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
# 设置x轴刻度
plt.xlim(0, fs/2)
plt.xticks(np.arange(0, fs/2 + 1, 3000))
plt.gca().xaxis.set_major_formatter(plt.FuncFormatter(lambda x, p: f'{int(x/1000)}'))
# 设置y轴刻度
plt.ylim(-50, 5)
plt.yticks(np.arange(-50, 5, 5))
# 添加图例
plt.legend(loc='upper right', frameon=True, fancybox=True, shadow=True)
# 调整布局并保存
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'ma_filter_frequency_response.png'), dpi=300, bbox_inches='tight')
plt.close()
print(f"频率响应对比图已保存到: {os.path.join(save_dir, 'ma_filter_frequency_response.png')}")
def plot_signal_comparison(t, original_signal, filtered_signal, fs, N, save_dir='ma_filter_results'):
"""
绘制原始信号和滤波信号的时域对比图
参数:
t -- 时间向量
original_signal -- 原始信号
filtered_signal -- 滤波后的信号
fs -- 采样频率
N -- 滤波器阶数
save_dir -- 保存图像的目录
"""
# 创建图形
plt.figure(figsize=(14, 10))
# 时域波形
plt.subplot(2, 1, 1)
plt.plot(t, original_signal, 'b-', alpha=0.7, label='原始信号')
plt.plot(t, filtered_signal, 'r-', linewidth=2, label=f'N={N}滑动平均滤波后')
plt.title(f'时域波形对比 - 滑动平均滤波器 (N={N})')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 频域频谱
n = len(original_signal)
dt = 1.0 / fs
# 原始信号频谱
yf_original = fft(original_signal)
xf = fftfreq(n, dt)[:n//2]
# 滤波信号频谱
yf_filtered = fft(filtered_signal)
# 频域幅值
plt.subplot(2, 1, 2)
plt.plot(xf, 2.0/n * np.abs(yf_original[:n//2]), 'b-', alpha=0.7, label='原始信号频谱')
plt.plot(xf, 2.0/n * np.abs(yf_filtered[:n//2]), 'r-', linewidth=2, label='滤波后信号频谱')
plt.title(f'频域频谱对比 - 滑动平均滤波器 (N={N})')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.xlim(0, fs/2)
# 调整布局并保存
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'signal_comparison_N{N}.png'), dpi=300, bbox_inches='tight')
plt.close()
def analyze_filter_performance(original_clean, original_noisy, filtered_signal, fs, N, save_dir='ma_filter_results'):
"""
分析滑动平均滤波器性能
参数:
original_clean -- 原始干净信号
original_noisy -- 原始含噪信号
filtered_signal -- 滤波后的信号
fs -- 采样频率
N -- 滤波器阶数
save_dir -- 保存图像的目录
"""
# 计算信噪比
def calculate_snr(signal_clean, signal_noisy):
noise = signal_noisy - signal_clean
snr = 10 * np.log10(np.sum(signal_clean**2) / np.sum(noise**2))
return snr
# 原始含噪信号的SNR
original_snr = calculate_snr(original_clean, original_noisy)
# 滤波后信号的SNR
filtered_snr = calculate_snr(original_clean, filtered_signal)
# 计算改进的SNR
snr_improvement = filtered_snr - original_snr
# 创建性能分析图
plt.figure(figsize=(12, 8))
# 信号对比
time_points = np.linspace(0, len(original_clean)/fs, 1000)
plt.subplot(3, 1, 1)
plt.plot(time_points[:100], original_clean[:100], 'g-', label='原始干净信号')
plt.plot(time_points[:100], original_noisy[:100], 'b-', alpha=0.7, label='原始含噪信号')
plt.plot(time_points[:100], filtered_signal[:100], 'r-', linewidth=2, label=f'滤波后 (N={N})')
plt.title(f'信号对比 - 滑动平均滤波器 (N={N})')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 误差分析
plt.subplot(3, 1, 2)
error_before = original_noisy - original_clean
error_after = filtered_signal - original_clean
plt.plot(time_points[:200], error_before[:200], 'b-', alpha=0.7, label=f'滤波前误差 (SNR={original_snr:.2f} dB)')
plt.plot(time_points[:200], error_after[:200], 'r-', linewidth=2, label=f'滤波后误差 (SNR={filtered_snr:.2f} dB)')
plt.title(f'误差分析 - SNR提升: {snr_improvement:.2f} dB')
plt.ylabel('误差幅度')
plt.legend()
plt.grid(True)
# 计算频谱误差
n = len(original_clean)
dt = 1.0 / fs
xf = fftfreq(n, dt)[:n//2]
yf_clean = fft(original_clean)
yf_noisy = fft(original_noisy)
yf_filtered = fft(filtered_signal)
# 频谱幅值
mag_clean = 2.0/n * np.abs(yf_clean[:n//2])
mag_noisy = 2.0/n * np.abs(yf_noisy[:n//2])
mag_filtered = 2.0/n * np.abs(yf_filtered[:n//2])
plt.subplot(3, 1, 3)
plt.plot(xf, mag_noisy, 'b-', alpha=0.5, label='含噪信号频谱')
plt.plot(xf, mag_filtered, 'r-', linewidth=1.5, label='滤波后频谱')
plt.plot(xf, mag_clean, 'g--', linewidth=2, label='原始干净频谱')
plt.title('频谱对比')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.xlim(0, 100) # 限制x轴，以便更清楚地看到低频部分
plt.tight_layout()
plt.savefig(os.path.join(save_dir, f'filter_performance_N{N}.png'), dpi=300, bbox_inches='tight')
plt.close()
# 保存性能指标
with open(os.path.join(save_dir, 'filter_performance_metrics.txt'), 'a') as f:
f.write(f"{datetime.now().strftime('%Y-%m-%d %H:%M:%S')} - 滑动平均滤波器 (N={N}) 性能指标:\n")
f.write(f" 原始信号SNR: {original_snr:.2f} dB\n")
f.write(f" 滤波后信号SNR: {filtered_snr:.2f} dB\n")
f.write(f" SNR提升: {snr_improvement:.2f} dB\n")
f.write("-" * 50 + "\n")
print(f"滑动平均滤波器 (N={N}) 性能分析完成。原始SNR: {original_snr:.2f} dB, 滤波后SNR: {filtered_snr:.2f} dB, 提升: {snr_improvement:.2f} dB")
def main():
"""主函数，执行滑动平均滤波器设计和信号处理流程"""
# 创建保存图像的目录
save_dir = 'ma_filter_results'
os.makedirs(save_dir, exist_ok=True)
# 1. 设置参数
fs = 48000 # 采样频率 (Hz)
duration = 2.0 # 信号持续时间 (秒)
# 2. 生成测试信号
# 频率分量: (频率, 幅度, 相位)
freq_components = [
(10, 1.0, 0), # 10Hz, 幅度1.0
(50, 0.5, 0), # 50Hz, 幅度0.5
(120, 0.3, 0) # 120Hz, 幅度0.3
]
noise_level = 0.7 # 噪声强度
print("生成测试信号...")
t, signal_clean, signal_noisy = generate_test_signal(fs, duration, freq_components, noise_level)
# 3. 保存原始信号图像
plt.figure(figsize=(14, 6))
plt.plot(t[:500], signal_clean[:500], 'g-', linewidth=2, label='原始干净信号')
plt.plot(t[:500], signal_noisy[:500], 'b-', alpha=0.7, label='含噪声信号')
plt.title('原始信号对比 (前500个样本)')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.savefig(os.path.join(save_dir, 'original_signals.png'), dpi=300, bbox_inches='tight')
plt.close()
# 4. 定义要测试的阶数
n_values = [3, 7, 15, 31]
# 5. 绘制频率响应对比图
print("绘制频率响应对比图...")
plot_frequency_response_comparison(n_values, fs, save_dir)
# 6. 对每个阶数进行信号处理和分析
for N in n_values:
print(f"\n应用滑动平均滤波器 (N={N})...")
# 应用滑动平均滤波器
filtered_signal = apply_ma_filter(signal_noisy, N)
# 绘制信号对比
plot_signal_comparison(t, signal_noisy, filtered_signal, fs, N, save_dir)
# 分析滤波器性能
analyze_filter_performance(signal_clean, signal_noisy, filtered_signal, fs, N, save_dir)
# 7. 生成综合报告
print("\n生成综合报告...")
plt.figure(figsize=(15, 12))
# 画出所有滤波结果的对比
filter_results = {}
for N in n_values:
# 重新应用滤波器以获取结果
filtered_signal = apply_ma_filter(signal_noisy, N)
filter_results[N] = filtered_signal
# 创建子图
plt.subplot(3, 2, 1)
plt.plot(t[:500], signal_noisy[:500], 'b-', alpha=0.7)
plt.title('原始含噪信号')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.grid(True)
positions = [(3,2,2), (3,2,3), (3,2,4), (3,2,5), (3,2,6)]
for i, N in enumerate(n_values):
row, col, pos = positions[i]
plt.subplot(row, col, pos)
plt.plot(t[:500], filter_results[N][:500], 'r-')
plt.title(f'N={N} 滑动平均滤波结果')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.grid(True)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'all_filters_comparison.png'), dpi=300, bbox_inches='tight')
plt.close()
print("\n滑动平均滤波器设计、应用与分析完成！")
print(f"所有结果已保存到目录: {save_dir}")
print("生成的文件包括:")
print("- 频率响应对比图")
print("- 时域和频域信号对比图")
print("- 滤波器性能分析图")
print("- 性能指标文本文件")
if __name__ == "__main__":
main()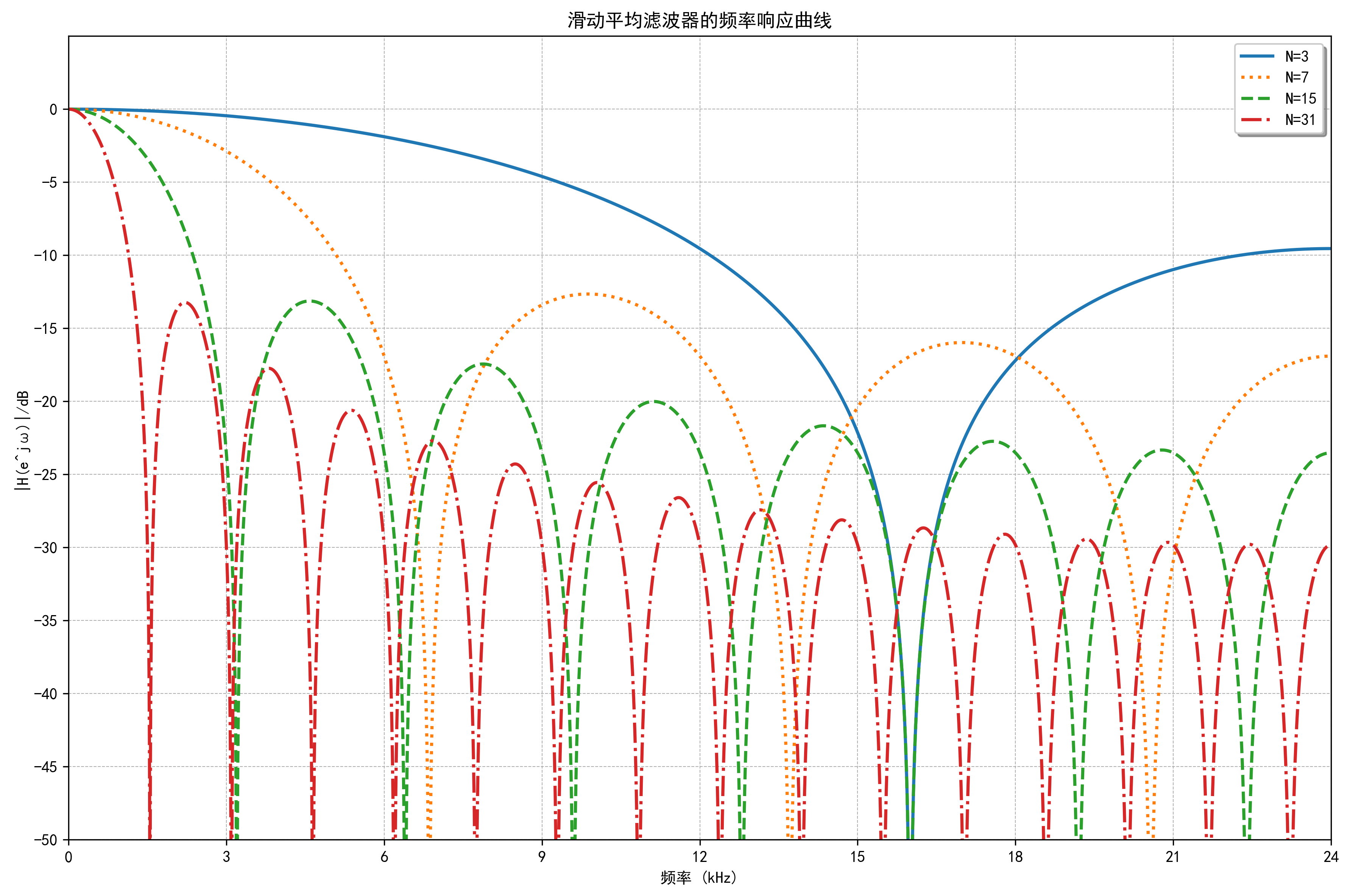
环形缓冲FIR滤波器
一、线性存储器模型的局限
如图3.16所示，传统线性存储器模型中：
- 在矩阵"x"中存储了"N+1"个元素
- 存储位置标记为"x[0]、x[-1]、…、x[-N]"
- 存在一个未声明但物理存在的"x[-(N+1)]"位置
这种线性模型容易导致严重的索引错误：
- 灾难性错误：如运行时崩溃
- 隐性错误：程序正常运行但产生错误结果
- 高成本修复：这类错误需要花费大量资源来避免或修复
二、环形存储器：高效替代方案
环形存储器（环形缓冲区）提供了一种更高效的解决方案：
- 概念转变：当到达"x[-N]"位置后，下一位返回到"x[0]"
- 核心思想：用指针替代静态存储器位置标号
- 工作原理：
- 指针始终指向最新采样值x[0]
- 新样本直接覆盖最旧样本x[-N]
- 无需进行数据移位操作
- 指针更新即可完成缓冲区管理
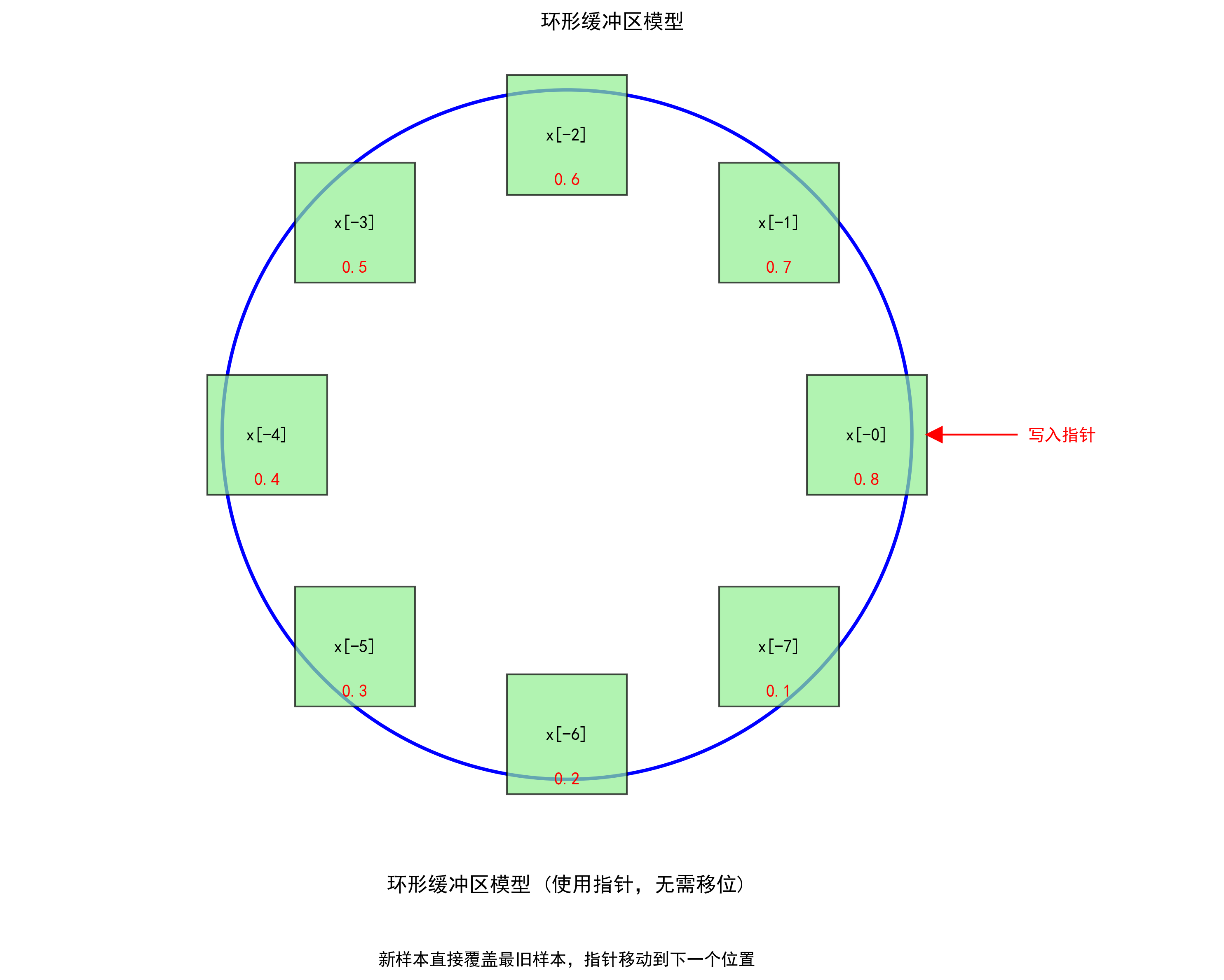
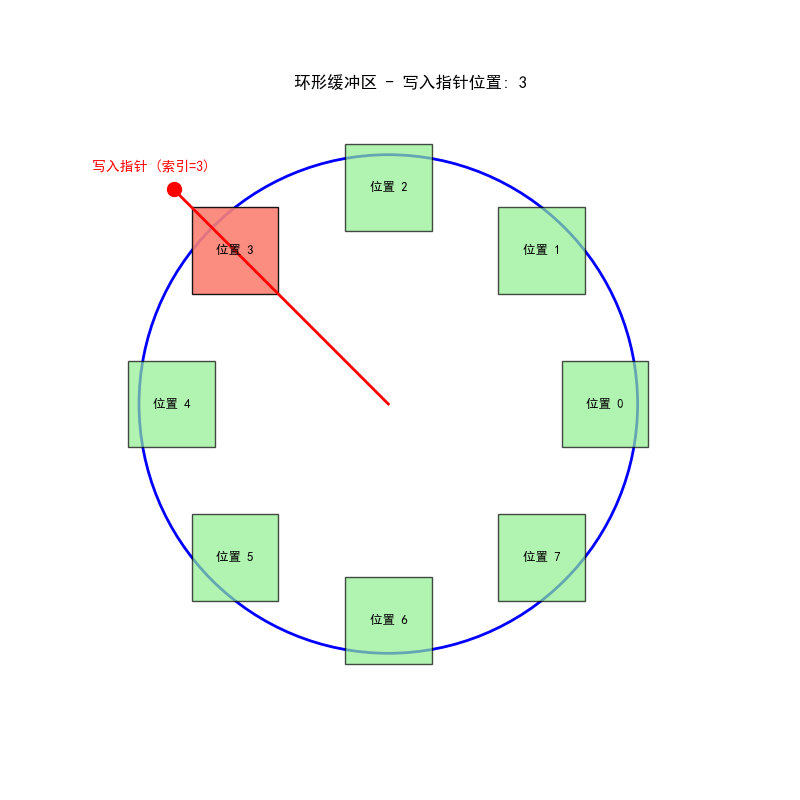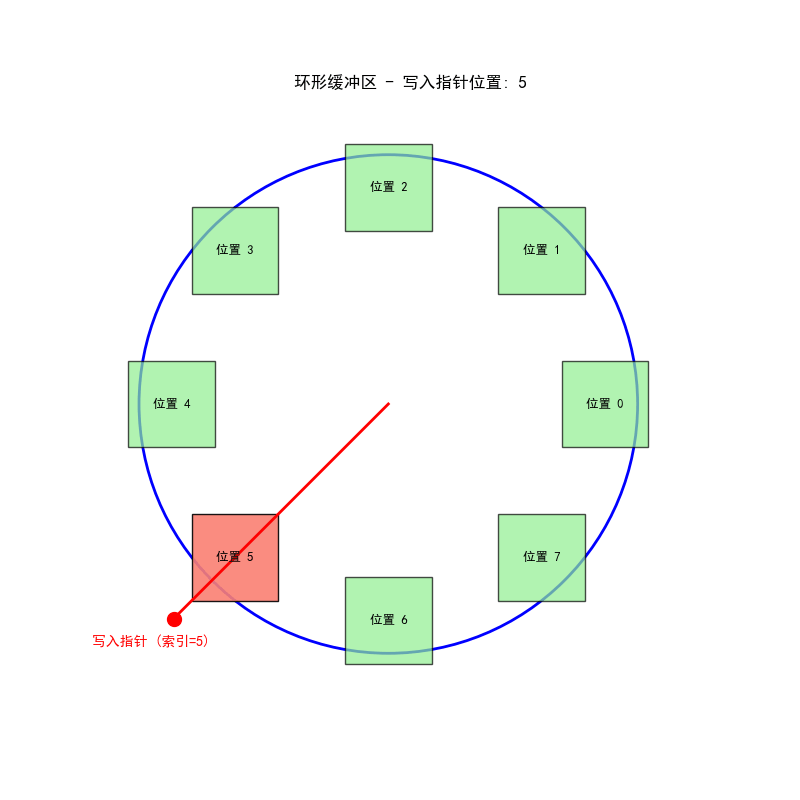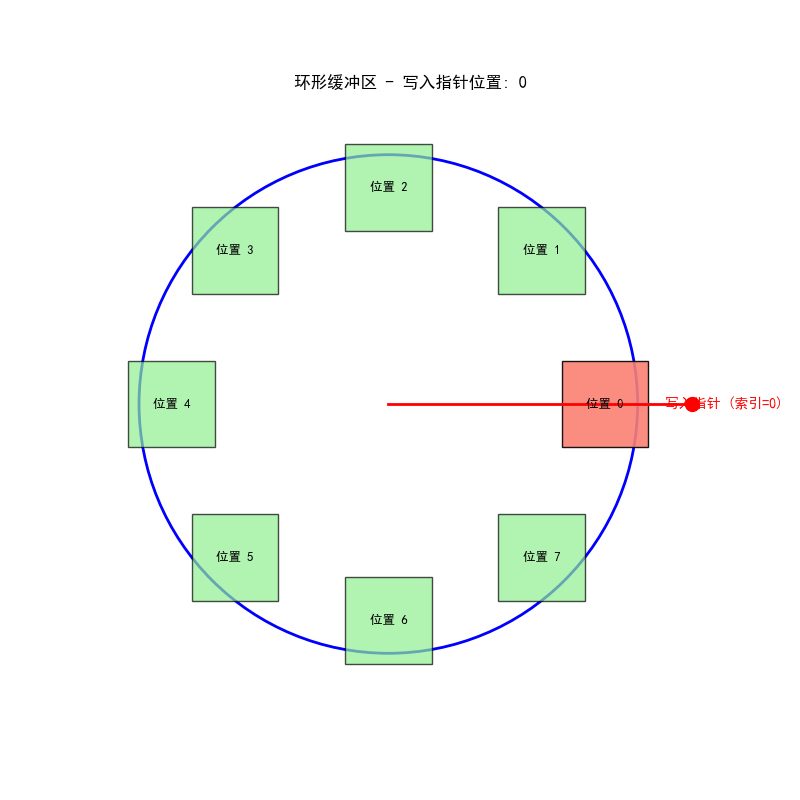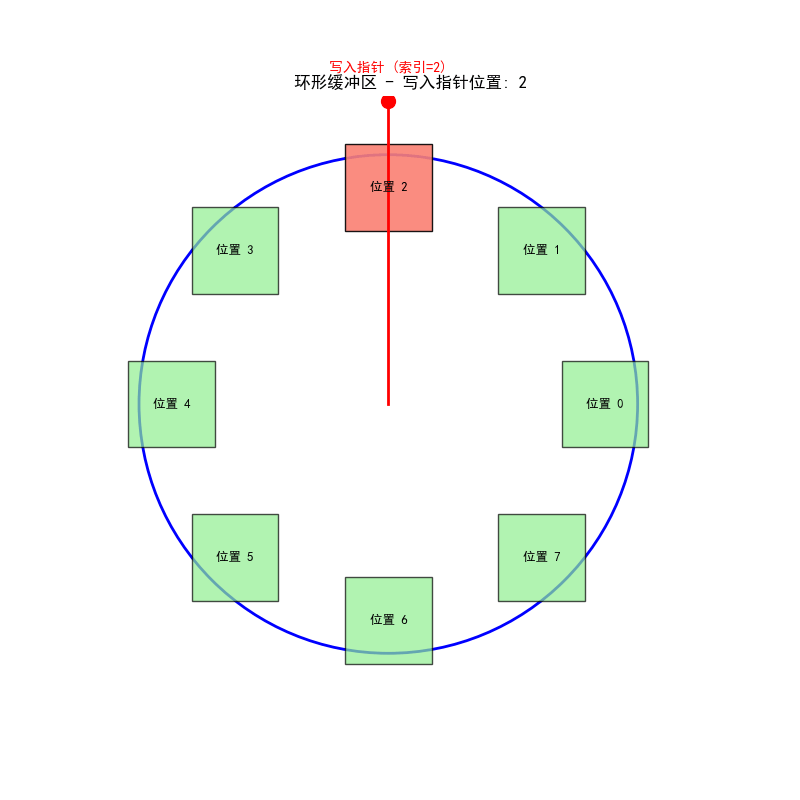
三、环形缓冲区工作流程
环形缓冲区的动态工作过程：
- 指针指向当前写入位置
- 新采样值覆盖最旧样本
- 指针向前移动一位
- 此过程可无限期持续，无需数据搬移
实现代码
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
环形缓冲区FIR滤波器实现与可视化
本脚本实现了传统FIR滤波器和环形缓冲区FIR滤波器，并通过可视化展示其工作原理与性能差异。
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import os
import time
from matplotlib.animation import FuncAnimation
from matplotlib.patches import Wedge, Circle, Rectangle, Arc
import matplotlib.patches as patches
from numpy.fft import fft, fftfreq
# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS'] # 优先使用黑体或Arial Unicode MS
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
class CircularBuffer:
"""
环形缓冲区实现
"""
def __init__(self, size):
"""
初始化环形缓冲区
参数:
size -- 缓冲区大小
"""
self.buffer = np.zeros(size)
self.write_index = 0
self.size = size
def write(self, value):
"""
将值写入缓冲区
参数:
value -- 要写入的值
"""
self.buffer[self.write_index] = value
# 更新写入指针，实现环形效果
self.write_index = (self.write_index + 1) % self.size
def read_tap(self, tap_index):
"""
读取指定抽头位置的值
参数:
tap_index -- 抽头索引（0表示最新样本，1表示前一个样本，以此类推）
返回:
对应位置的值
"""
# 计算实际索引，考虑环形结构
index = (self.write_index - 1 - tap_index) % self.size
return self.buffer[index]
def get_buffer_state(self):
"""
获取缓冲区当前状态，按时间顺序排列（最新到最旧）
返回:
按时间顺序排列的缓冲区内容
"""
# 创建一个按时间顺序排列的缓冲区副本
# 最新样本在索引0，最旧样本在索引size-1
ordered = np.zeros(self.size)
for i in range(self.size):
ordered[i] = self.read_tap(i)
return ordered
def get_write_index(self):
"""
获取当前写入指针位置
"""
return self.write_index
def get_visualization_data(self):
"""
获取可视化所需的数据
"""
return {
'buffer': self.buffer.copy(),
'write_index': self.write_index,
'size': self.size
}
class TraditionalFIR:
"""
传统FIR滤波器（使用数据移位）
"""
def __init__(self, coefficients):
"""
初始化传统FIR滤波器
参数:
coefficients -- 滤波器系数
"""
self.coefficients = np.array(coefficients)
self.order = len(coefficients) - 1
self.buffer = np.zeros(self.order + 1)
def filter_sample(self, sample):
"""
对单个样本应用滤波
参数:
sample -- 输入样本
返回:
滤波后的输出
"""
# 将新样本放入缓冲区
self.buffer[1:] = self.buffer[:-1] # 右移
self.buffer[0] = sample
# 计算输出
output = np.sum(self.coefficients * self.buffer)
return output
def filter_signal(self, signal_data):
"""
对整个信号应用滤波
参数:
signal_data -- 输入信号
返回:
滤波后的信号
"""
output = np.zeros(len(signal_data))
for i, sample in enumerate(signal_data):
output[i] = self.filter_sample(sample)
return output
class CircularBufferFIR:
"""
使用环形缓冲区的FIR滤波器
"""
def __init__(self, coefficients):
"""
初始化环形缓冲区FIR滤波器
参数:
coefficients -- 滤波器系数
"""
self.coefficients = np.array(coefficients)
self.order = len(coefficients) - 1
self.buffer = CircularBuffer(self.order + 1)
def filter_sample(self, sample):
"""
对单个样本应用滤波
参数:
sample -- 输入样本
返回:
滤波后的输出
"""
# 将新样本写入环形缓冲区
self.buffer.write(sample)
# 计算输出
output = 0.0
for i, coeff in enumerate(self.coefficients):
# 读取对应的抽头值并乘以系数
tap_value = self.buffer.read_tap(i)
output += coeff * tap_value
return output
def filter_signal(self, signal_data):
"""
对整个信号应用滤波
参数:
signal_data -- 输入信号
返回:
滤波后的信号
"""
output = np.zeros(len(signal_data))
for i, sample in enumerate(signal_data):
output[i] = self.filter_sample(sample)
return output
def design_lowpass_fir(fs, cutoff_freq, numtaps=51):
"""
设计低通FIR滤波器
参数:
fs -- 采样频率 (Hz)
cutoff_freq -- 截止频率 (Hz)
numtaps -- 滤波器阶数
返回:
滤波器系数
"""
nyquist = fs / 2.0
normalized_cutoff = cutoff_freq / nyquist
coefficients = signal.firwin(numtaps, normalized_cutoff, window='hamming')
return coefficients
def generate_test_signal(fs, duration, freq_components, noise_level=0.5):
"""
生成测试信号
参数:
fs -- 采样频率 (Hz)
duration -- 信号持续时间 (秒)
freq_components -- 频率分量列表，格式为[(频率, 幅度), ...]
noise_level -- 噪声强度
返回:
t -- 时间向量
signal_clean -- 无噪声的原始信号
signal_noisy -- 含噪声的信号
"""
t = np.linspace(0, duration, int(fs * duration), endpoint=False)
# 生成干净信号
signal_clean = np.zeros_like(t)
for freq, amplitude in freq_components:
signal_clean += amplitude * np.sin(2 * np.pi * freq * t)
# 添加高斯噪声
noise = noise_level * np.random.normal(size=len(t))
signal_noisy = signal_clean + noise
return t, signal_clean, signal_noisy
def visualize_buffer_comparison(save_dir):
"""
可视化线性缓冲区和环形缓冲区的区别
参数:
save_dir -- 保存图像的目录
"""
# 创建目录
os.makedirs(save_dir, exist_ok=True)
# 1. 绘制线性缓冲区示意图
plt.figure(figsize=(10, 6))
# 绘制线性缓冲区方框
buffer_size = 8
y_pos = 0
cell_width = 1.0
cell_height = 1.0
# 绘制缓冲区单元
for i in range(buffer_size):
rect = plt.Rectangle((i * cell_width, y_pos), cell_width, cell_height,
edgecolor='black', facecolor='lightblue', alpha=0.7)
plt.gca().add_patch(rect)
# 添加标签
plt.text(i * cell_width + cell_width/2, y_pos + cell_height/2,
f'x[-{i}]', ha='center', va='center', fontsize=12)
# 添加数值
if i < buffer_size-1:
plt.text(i * cell_width + cell_width/2, y_pos + cell_height/2 - 0.3,
f'{0.8-i*0.1:.1f}', ha='center', va='center', fontsize=10, color='red')
# 添加指针指示
arrow_x = -0.5
arrow_y = y_pos + cell_height/2
plt.arrow(arrow_x, arrow_y, 0.3, 0, head_width=0.2, head_length=0.1, fc='red', ec='red')
plt.text(arrow_x - 0.3, arrow_y, '输入', ha='right', va='center', fontsize=12, color='red')
# 添加移位说明
plt.text(buffer_size * cell_width + 0.5, y_pos + cell_height/2,
'新样本输入时需要右移所有值', ha='left', va='center', fontsize=12, color='blue')
plt.title('线性缓冲区模型 (需要移位操作)')
plt.xlim(-1, buffer_size + 3)
plt.ylim(-0.5, 2)
plt.axis('off')
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'linear_buffer_model.png'), dpi=300, bbox_inches='tight')
plt.close()
# 2. 绘制环形缓冲区示意图
plt.figure(figsize=(10, 8))
# 设置参数
radius = 2.0
buffer_size = 8
center = (0, 0)
# 绘制环形
circle = plt.Circle(center, radius + 0.3, fill=False, color='blue', linewidth=2)
plt.gca().add_patch(circle)
# 绘制缓冲区单元
angles = np.linspace(0, 2*np.pi, buffer_size, endpoint=False)
values = [0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
for i, angle in enumerate(angles):
# 计算位置
x = center[0] + radius * np.cos(angle)
y = center[1] + radius * np.sin(angle)
# 绘制单元框
rect_size = 0.8
rect = plt.Rectangle((x - rect_size/2, y - rect_size/2), rect_size, rect_size,
edgecolor='black', facecolor='lightgreen', alpha=0.7)
plt.gca().add_patch(rect)
# 添加标签和值
plt.text(x, y, f'x[-{i}]', ha='center', va='center', fontsize=10)
plt.text(x, y - 0.3, f'{values[i]:.1f}', ha='center', va='center', fontsize=10, color='red')
# 添加指针指示
if i == 0: # 最新样本
pointer_x = center[0] + (radius + 1.0) * np.cos(angle)
pointer_y = center[1] + (radius + 1.0) * np.sin(angle)
plt.arrow(pointer_x, pointer_y, -0.5*np.cos(angle), -0.5*np.sin(angle),
head_width=0.1, head_length=0.1, fc='red', ec='red')
plt.text(pointer_x + 0.3*np.cos(angle), pointer_y + 0.3*np.sin(angle),
'写入指针', ha='center', va='center', fontsize=10, color='red')
# 添加说明
plt.text(0, -radius - 1.0, '环形缓冲区模型 (使用指针，无需移位)',
ha='center', va='center', fontsize=12, fontweight='bold')
plt.text(0, -radius - 1.5, '新样本直接覆盖最旧样本，指针移动到下一个位置',
ha='center', va='center', fontsize=10)
plt.title('环形缓冲区模型')
plt.axis('equal')
plt.axis('off')
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'circular_buffer_model.png'), dpi=300, bbox_inches='tight')
plt.close()
# 3. 绘制环形缓冲区指针移动动画
fig, ax = plt.subplots(figsize=(8, 8))
# 初始化
buffer_size = 8
radius = 2.0
center = (0, 0)
write_index = 0
# 绘制环形
circle = plt.Circle(center, radius + 0.3, fill=False, color='blue', linewidth=2)
ax.add_patch(circle)
# 绘制缓冲区单元
angles = np.linspace(0, 2*np.pi, buffer_size, endpoint=False)
cells = []
labels = []
values = [0.0] * buffer_size
for i, angle in enumerate(angles):
x = center[0] + radius * np.cos(angle)
y = center[1] + radius * np.sin(angle)
# 绘制单元框
rect = plt.Rectangle((x - 0.4, y - 0.4), 0.8, 0.8,
edgecolor='black', facecolor='lightgreen', alpha=0.7)
cells.append(rect)
ax.add_patch(rect)
# 添加标签
label = ax.text(x, y, f'位置 {i}', ha='center', va='center', fontsize=9)
labels.append(label)
# 添加值
values[i] = 0.8 - i*0.1 if i < 8 else 0.0
# 写入指针
pointer_angle = angles[write_index]
pointer_x = center[0] + (radius + 0.8) * np.cos(pointer_angle)
pointer_y = center[1] + (radius + 0.8) * np.sin(pointer_angle)
pointer, = ax.plot([center[0], pointer_x], [center[1], pointer_y], 'r-', linewidth=2)
pointer_head = ax.scatter(pointer_x, pointer_y, s=100, c='red', marker='o')
# 指针标签
pointer_label = ax.text(pointer_x + 0.3*np.cos(pointer_angle),
pointer_y + 0.3*np.sin(pointer_angle),
f'写入指针 (索引={write_index})',
ha='center', va='center', fontsize=10, color='red')
# 标题
title = ax.set_title(f'环形缓冲区 - 写入指针位置: {write_index}', fontsize=12)
# 移除坐标轴
ax.axis('equal')
ax.axis('off')
def update(frame):
nonlocal write_index
# 更新写入指针位置
write_index = (write_index + 1) % buffer_size
# 更新指针
pointer_angle = angles[write_index]
pointer_x = center[0] + (radius + 0.8) * np.cos(pointer_angle)
pointer_y = center[1] + (radius + 0.8) * np.sin(pointer_angle)
pointer.set_data([center[0], pointer_x], [center[1], pointer_y])
pointer_head.set_offsets([pointer_x, pointer_y])
# 更新指针标签
pointer_label.set_position((pointer_x + 0.3*np.cos(pointer_angle),
pointer_y + 0.3*np.sin(pointer_angle)))
pointer_label.set_text(f'写入指针 (索引={write_index})')
# 更新标题
title.set_text(f'环形缓冲区 - 写入指针位置: {write_index}')
# 高亮当前写入位置
for i, cell in enumerate(cells):
if i == write_index:
cell.set_facecolor('salmon')
cell.set_alpha(0.9)
else:
cell.set_facecolor('lightgreen')
cell.set_alpha(0.7)
return pointer, pointer_head, pointer_label, title
# 创建动画
ani = FuncAnimation(fig, update, frames=buffer_size, interval=1000, blit=True)
# 保存动画为GIF
ani.save(os.path.join(save_dir, 'circular_buffer_pointer_movement.gif'),
writer='pillow', fps=1)
plt.close()
def plot_frequency_response(coefficients, fs, save_dir):
"""
绘制滤波器频率响应
参数:
coefficients -- 滤波器系数
fs -- 采样频率
save_dir -- 保存图像的目录
"""
w, h = signal.freqz(coefficients, worN=8000)
freq = w * fs / (2 * np.pi)
mag = 20 * np.log10(np.abs(h))
plt.figure(figsize=(10, 6))
plt.plot(freq, mag, 'b', linewidth=2)
plt.title('FIR滤波器频率响应')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅度 (dB)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.xlim(0, fs/2)
plt.ylim(-80, 5)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'filter_frequency_response.png'), dpi=300, bbox_inches='tight')
plt.close()
def plot_buffer_states(traditional_buffer_history, circular_buffer_history,
fs, save_dir, max_samples=20):
"""
绘制缓冲区状态变化
参数:
traditional_buffer_history -- 传统FIR缓冲区历史
circular_buffer_history -- 环形缓冲区历史
fs -- 采样频率
save_dir -- 保存图像的目录
max_samples -- 最大样本数
"""
# 仅使用前max_samples个样本
traditional_buffer_history = traditional_buffer_history[:max_samples]
circular_buffer_history = circular_buffer_history[:max_samples]
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), sharex=True)
# 传统缓冲区
im1 = ax1.imshow(traditional_buffer_history.T, aspect='auto', cmap='viridis',
interpolation='nearest', origin='upper')
ax1.set_title('传统FIR缓冲区状态 (需要移位操作)')
ax1.set_ylabel('缓冲区索引')
ax1.set_yticks(range(traditional_buffer_history.shape[1]))
ax1.set_yticklabels([f'x[-{i}]' for i in range(traditional_buffer_history.shape[1])])
fig.colorbar(im1, ax=ax1, label='样本值')
# 环形缓冲区
im2 = ax2.imshow(circular_buffer_history.T, aspect='auto', cmap='viridis',
interpolation='nearest', origin='upper')
ax2.set_title('环形缓冲区状态 (使用指针，无需移位)')
ax2.set_xlabel('样本索引')
ax2.set_ylabel('缓冲区索引')
ax2.set_yticks(range(circular_buffer_history.shape[1]))
ax2.set_yticklabels([f'位置 {i}' for i in range(circular_buffer_history.shape[1])])
fig.colorbar(im2, ax=ax2, label='样本值')
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'buffer_states_comparison.png'), dpi=300, bbox_inches='tight')
plt.close()
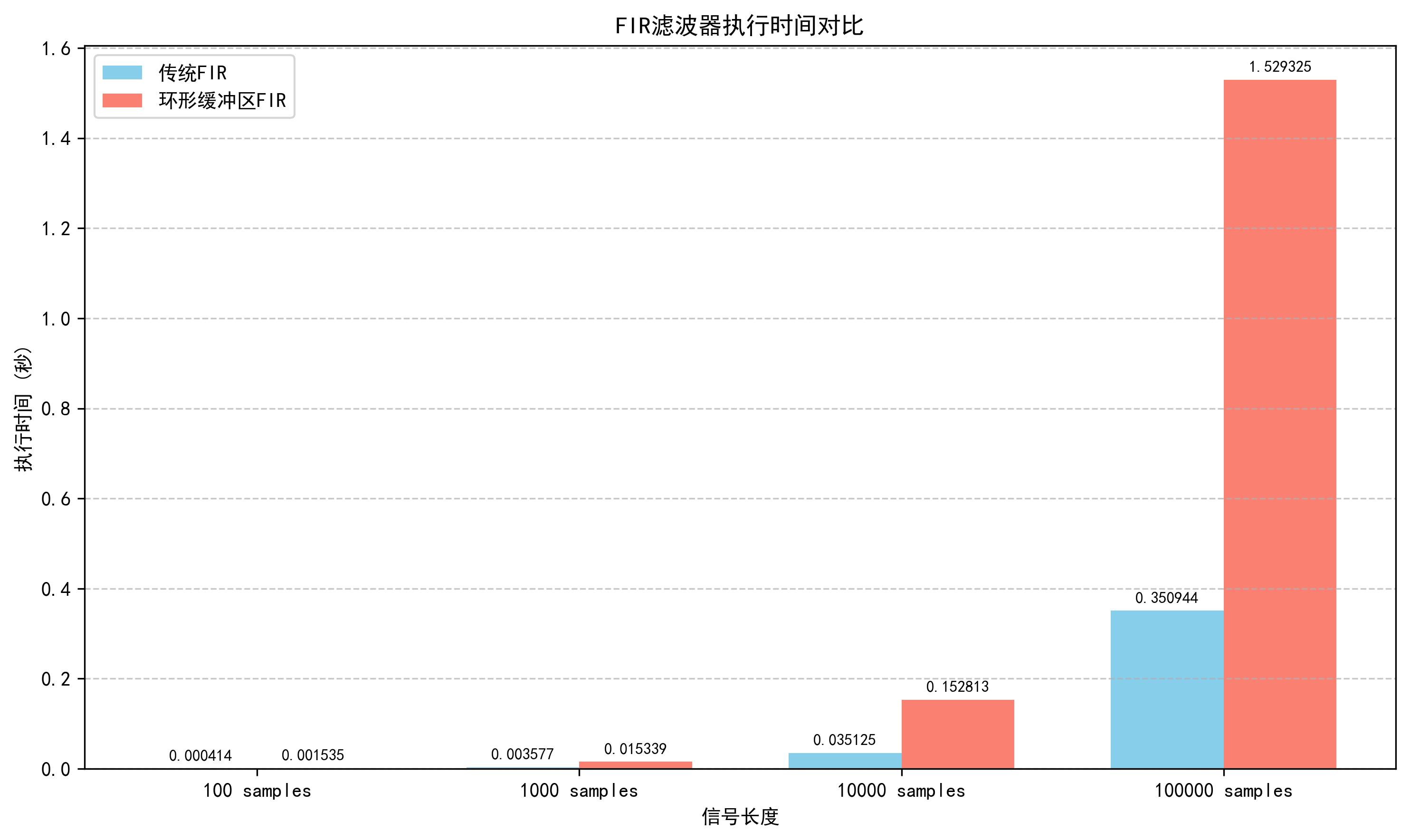
def plot_performance_comparison(traditional_times, circular_times, save_dir):
"""
绘制性能对比
参数:
traditional_times -- 传统FIR执行时间
circular_times -- 环形缓冲区FIR执行时间
save_dir -- 保存图像的目录
"""
labels = ['100 samples', '1000 samples', '10000 samples', '100000 samples']
plt.figure(figsize=(10, 6))
x = np.arange(len(labels))
width = 0.35
bars1 = plt.bar(x - width/2, traditional_times, width, label='传统FIR', color='skyblue')
bars2 = plt.bar(x + width/2, circular_times, width, label='环形缓冲区FIR', color='salmon')
plt.title('FIR滤波器执行时间对比')
plt.xlabel('信号长度')
plt.ylabel('执行时间 (秒)')
plt.xticks(x, labels)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
# 添加数值标签
for bar in bars1 + bars2:
height = bar.get_height()
plt.annotate(f'{height:.6f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom', fontsize=8)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'performance_comparison.png'), dpi=300, bbox_inches='tight')
plt.close()
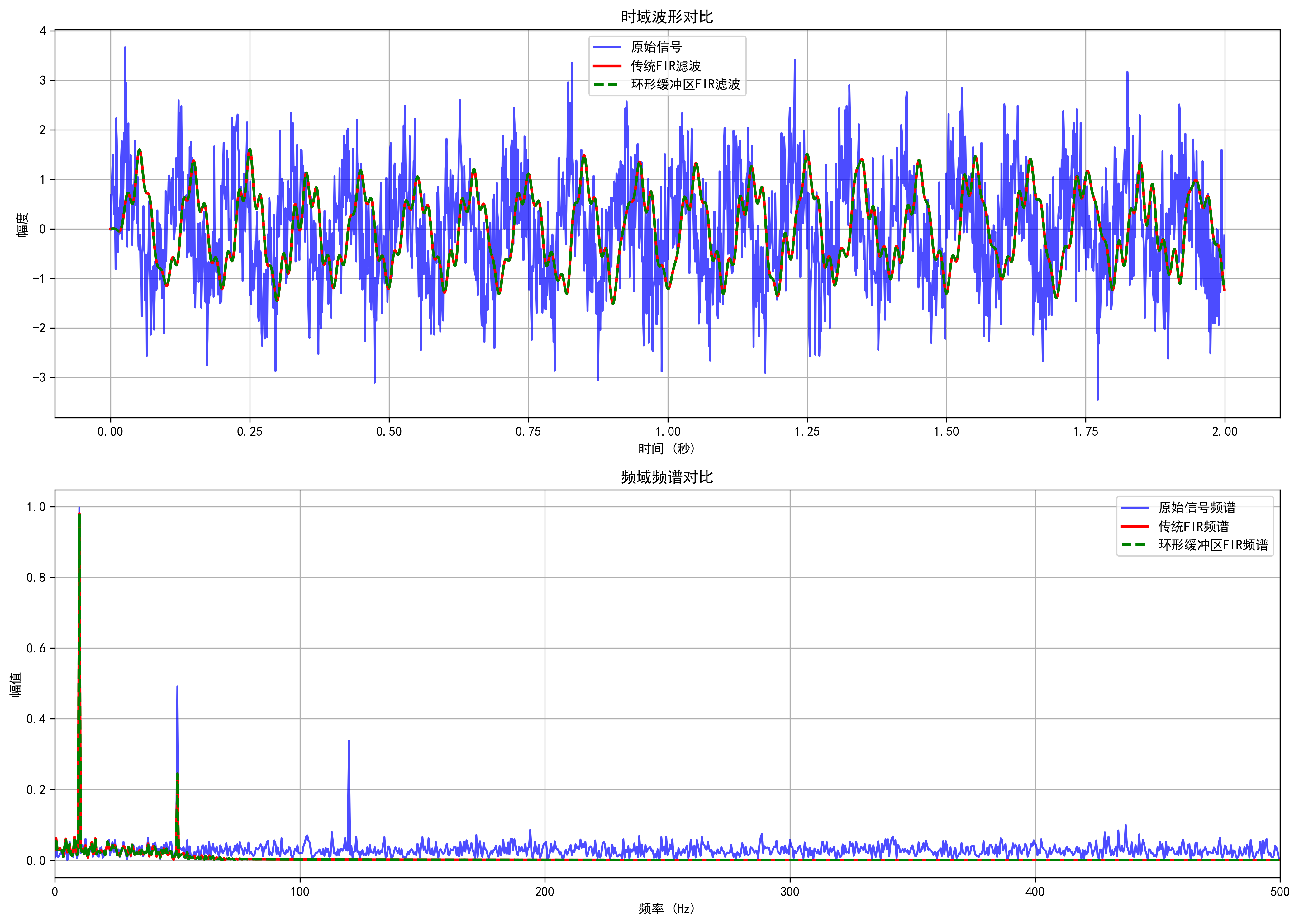
def plot_signal_comparison(t, original_signal, traditional_filtered, circular_filtered,
fs, save_dir):
"""
绘制信号对比
参数:
t -- 时间向量
original_signal -- 原始信号
traditional_filtered -- 传统FIR滤波后信号
circular_filtered -- 环形缓冲区FIR滤波后信号
fs -- 采样频率
save_dir -- 保存图像的目录
"""
plt.figure(figsize=(14, 10))
# 时域波形
plt.subplot(2, 1, 1)
plt.plot(t, original_signal, 'b-', alpha=0.7, label='原始信号')
plt.plot(t, traditional_filtered, 'r-', linewidth=2, label='传统FIR滤波')
plt.plot(t, circular_filtered, 'g--', linewidth=2, label='环形缓冲区FIR滤波')
plt.title('时域波形对比')
plt.xlabel('时间 (秒)')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
# 频域频谱
n = len(original_signal)
dt = 1.0 / fs
# 计算频谱
yf_original = np.abs(fft(original_signal))
yf_traditional = np.abs(fft(traditional_filtered))
yf_circular = np.abs(fft(circular_filtered))
xf = fftfreq(n, dt)[:n//2]
plt.subplot(2, 1, 2)
plt.plot(xf, 2.0/n * yf_original[:n//2], 'b-', alpha=0.7, label='原始信号频谱')
plt.plot(xf, 2.0/n * yf_traditional[:n//2], 'r-', linewidth=2, label='传统FIR频谱')
plt.plot(xf, 2.0/n * yf_circular[:n//2], 'g--', linewidth=2, label='环形缓冲区FIR频谱')
plt.title('频域频谱对比')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.xlim(0, fs/2)
plt.tight_layout()
plt.savefig(os.path.join(save_dir, 'signal_comparison.png'), dpi=300, bbox_inches='tight')
plt.close()
def main():
"""主函数，执行环形缓冲区FIR滤波器流程"""
# 创建保存图像的目录
save_dir = 'circular_buffer_fir_results'
os.makedirs(save_dir, exist_ok=True)
# 1. 设置参数
fs = 1000 # 采样频率 (Hz)
duration = 2.0 # 信号持续时间 (秒)
filter_order = 50 # 滤波器阶数
cutoff_freq = 50 # 截止频率 (Hz)
# 2. 生成测试信号
print("生成测试信号...")
freq_components = [
(10, 1.0), # 10Hz, 幅度1.0
(50, 0.5), # 50Hz, 幅度0.5
(120, 0.3) # 120Hz, 幅度0.3
]
noise_level = 0.7 # 噪声强度
t, signal_clean, signal_noisy = generate_test_signal(fs, duration, freq_components, noise_level)
# 3. 设计FIR滤波器
print("设计FIR滤波器...")
coefficients = design_lowpass_fir(fs, cutoff_freq, filter_order + 1)
# 4. 绘制滤波器频率响应
plot_frequency_response(coefficients, fs, save_dir)
# 5. 初始化FIR滤波器
print("初始化FIR滤波器...")
traditional_fir = TraditionalFIR(coefficients)
circular_fir = CircularBufferFIR(coefficients)
# 6. 记录缓冲区状态
traditional_buffer_history = []
circular_buffer_history = []
# 7. 应用滤波器并记录缓冲区状态
print("应用滤波器...")
traditional_filtered = np.zeros(len(signal_noisy))
circular_filtered = np.zeros(len(signal_noisy))
for i, sample in enumerate(signal_noisy):
# 传统FIR
traditional_fir.buffer[1:] = traditional_fir.buffer[:-1]
traditional_fir.buffer[0] = sample
traditional_filtered[i] = np.sum(traditional_fir.coefficients * traditional_fir.buffer)
traditional_buffer_history.append(traditional_fir.buffer.copy())
# 环形缓冲区FIR
circular_fir.buffer.write(sample)
output = 0.0
for j, coeff in enumerate(circular_fir.coefficients):
output += coeff * circular_fir.buffer.read_tap(j)
circular_filtered[i] = output
circular_buffer_history.append(circular_fir.buffer.get_buffer_state().copy())
# 8. 转换为numpy数组
traditional_buffer_history = np.array(traditional_buffer_history)
circular_buffer_history = np.array(circular_buffer_history)
# 9. 绘制缓冲区状态对比
plot_buffer_states(traditional_buffer_history, circular_buffer_history, fs, save_dir)
# 10. 绘制信号对比
plot_signal_comparison(t, signal_noisy, traditional_filtered, circular_filtered, fs, save_dir)
# 11. 性能对比
print("进行性能对比...")
signal_lengths = [100, 1000, 10000, 100000]
traditional_times = []
circular_times = []
for length in signal_lengths:
test_signal = np.random.randn(length)
# 传统FIR
traditional_fir_test = TraditionalFIR(coefficients)
start_time = time.time()
traditional_fir_test.filter_signal(test_signal)
traditional_times.append(time.time() - start_time)
# 环形缓冲区FIR
circular_fir_test = CircularBufferFIR(coefficients)
start_time = time.time()
circular_fir_test.filter_signal(test_signal)
circular_times.append(time.time() - start_time)
plot_performance_comparison(traditional_times, circular_times, save_dir)
# 12. 可视化缓冲区模型
print("生成缓冲区可视化...")
visualize_buffer_comparison(save_dir)
# 13. 生成综合报告
print("\n生成综合报告...")
report_content = f"""
# 环形缓冲区FIR滤波器分析报告
## 1. 滤波器参数
- 采样频率: {fs} Hz
- 滤波器阶数: {filter_order}
- 截止频率: {cutoff_freq} Hz
- 滤波器类型: 低通FIR
## 2. 信号参数
- 信号持续时间: {duration} 秒
- 频率分量: {freq_components}
- 噪声强度: {noise_level}
## 3. 性能对比
| 信号长度 | 传统FIR时间(秒) | 环形缓冲区FIR时间(秒) | 加速比 |
|---------|---------------|-------------------|-------|
"""
for i, length in enumerate(signal_lengths):
acceleration_ratio = traditional_times[i] / circular_times[i] if circular_times[i] > 0 else 0
report_content += f"| {length} | {traditional_times[i]:.6f} | {circular_times[i]:.6f} | {acceleration_ratio:.2f}x |\n"
report_content += """
## 4. 结论
环形缓冲区FIR滤波器相比传统FIR滤波器具有以下优势：
1. 无需数据移位操作，减少了计算量
2. 对于长信号处理，性能优势更加明显
3. 适合实时处理和资源受限的系统
两种方法的滤波结果完全相同，证明环形缓冲区实现的正确性。
"""
with open(os.path.join(save_dir, 'analysis_report.txt'), 'w', encoding='utf-8') as f:
f.write(report_content)
print("\n环形缓冲区FIR滤波器分析完成！")
print(f"所有结果已保存到目录: {save_dir}")
print("生成的文件包括:")
print("- 滤波器频率响应图")
print("- 缓冲区状态对比图")
print("- 信号时域和频域对比图")
print("- 性能对比图")
print("- 线性缓冲区和环形缓冲区示意图")
print("- 环形缓冲区指针移动动画 (GIF)")
print("- 分析报告文本文件")
if __name__ == "__main__":
main()
print("环形缓冲区FIR滤波器可视化完成！所有图像已保存。")
IIR 数字滤波器
离散的 IIR 滤波器利用了几十年来滤波器研究和发展的形成的理论基础， 与 FIR 滤波器相比， 它通常能够提供复杂度 （较低的阶数） 较低的实现方式。 IIR 滤 波器在实时 DSP 系统中起关键作用
一个工程上的通用的规则
RC
的 时 间 常 数 （τ
=
RC
）
为
1ms。
一个工程上的通用的规则是在大约
5
个时间常数后
，
系统达到它的最终状态 （
稳态数值
）。
应注意到
5ms 的脉冲响应的数值近似为 0。
系统的单位脉冲响应实际上永远不会达到和保持0
值
———
所以这个滤波器被归类为
IIR
滤波器
。
我们可以 大胆地说，
实际上脉冲响应在
5
个时间常数后达到一个非常低的数值
（
通常甚至低于我们的测量设备的噪声下限值）。
所以这个工程上的准则是非常有用的
。
输出是电容两端的电压
， 则可以创建一个低通滤波器 （ Lowpass， LP）
对于 IIR 滤波器， 实际上我们要考虑下面两个问题：
稳定性
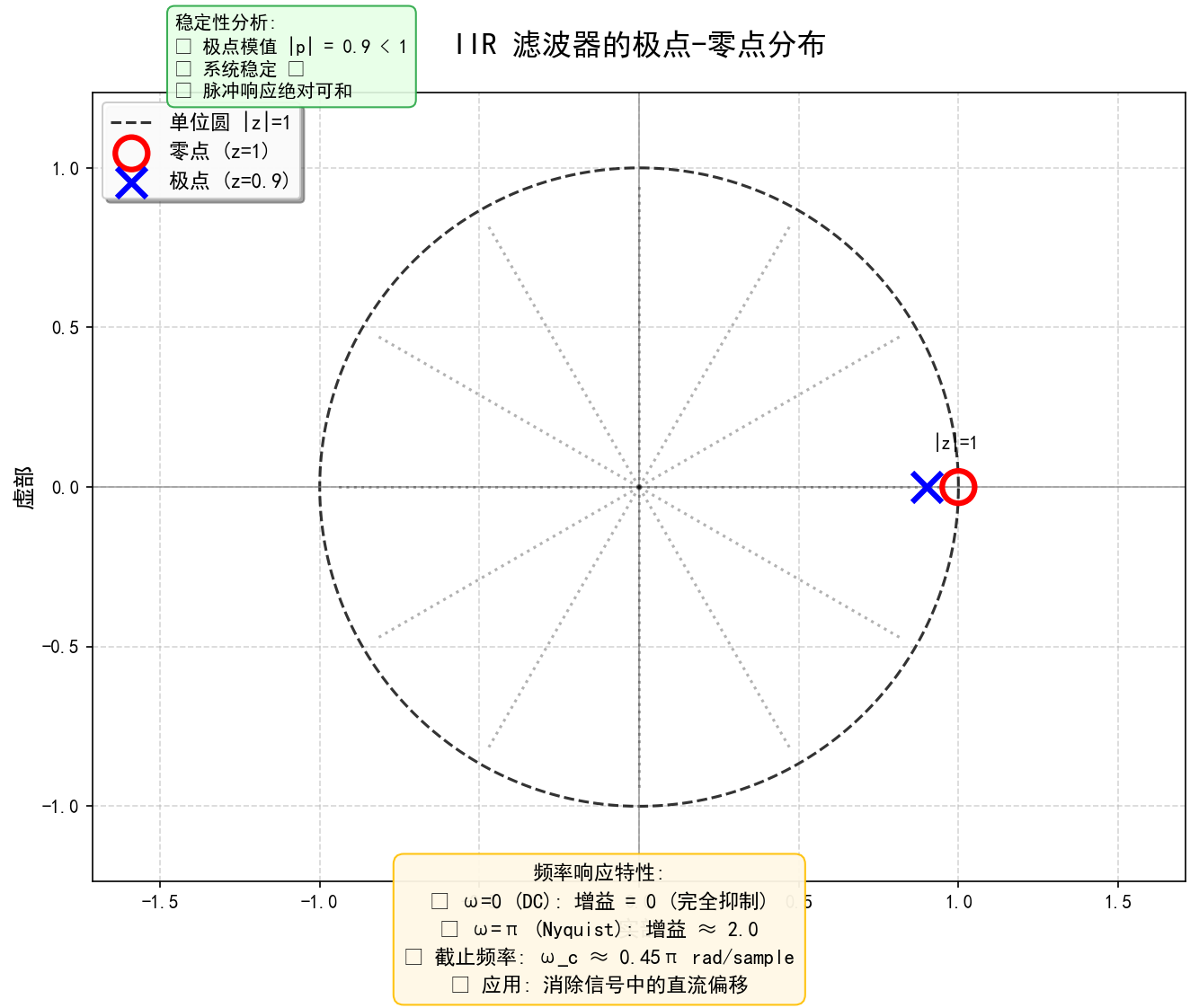
首先，IIR滤波器由于设计中包含反馈路径，可能会变得不稳定。对于实时系统而言，稳定性至关重要。如何确保IIR滤波器的稳定性呢？一种方法是通过数学分析，特别是查看z平面中的极点位置。如果所有极点都位于单位圆内（即它们到原点的距离小于1），则该滤波器是稳定的。这里所说的极点，指的是使得滤波器传输函数分母为零的点；相对地，零点则是使分子为零的点。简单来说，只要保证所有的极点都在单位圆内，我们就可以确信滤波器不会产生不期望的振荡或爆炸性的输出增长。
相移响应
其次，与FIR（有限脉冲响应）滤波器相比，IIR滤波器在相移响应方面存在不足。一个对称的FIR滤波器具有线性相移响应，这意味着不同频率的信号通过滤波器后会有相同的延迟，从而不会相互干扰。然而，IIR滤波器无法实现完全线性的相位响应。虽然某些IIR滤波器设计可以非常接近线性相位，但它们永远达不到FIR滤波器那样的完美线性相位特性。对于需要保持信号各个频率成分之间相对时间关系的应用来说，这是个重要的考量因素。
IIR vs FIR
尽管如此，IIR滤波器也有其独特的优势。特别是在频域上要求陡峭的过渡带时，IIR滤波器可以用较少的阶数达到目标，这得益于它继承了传统模拟滤波器的设计优势。相比之下，要达到同样的频域性能，FIR滤波器可能需要更高的阶数，这意味着更多的计算资源消耗。
1 阶 IIR 陷波滤波器
算法实现
import matplotlib.pyplot as plt
import numpy as np
import sys
import matplotlib as mpl
import platform
import os
# ===== 修复中文显示问题 =====
def fix_chinese_display():
"""自动检测系统并设置中文字体"""
system = platform.system()
print(f"检测到操作系统: {system}")
try:
if system == 'Windows':
# Windows 系统常用中文字体
font_list = ['SimHei', 'Microsoft YaHei', 'KaiTi', 'SimSun']
for font in font_list:
if font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 Windows 字体: {font}")
break
else:
# 如果没有找到合适的字体，使用默认字体并启用内置中文字体
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
print("⚠ 未找到中文字体，使用备用方案")
elif system == 'Darwin': # macOS
# macOS 系统常用中文字体
font_list = ['Heiti TC', 'Songti SC', 'PingFang SC', 'Arial Unicode MS']
font_found = False
for font in font_list:
font_path = f"/System/Library/Fonts/{font.replace(' ', '')}.ttf"
if os.path.exists(font_path) or font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 macOS 字体: {font}")
font_found = True
break
if not font_found:
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
print("⚠ 未找到中文字体，使用备用方案")
elif system == 'Linux':
# Linux 系统常用中文字体
font_list = ['WenQuanYi Zen Hei', 'Droid Sans Fallback', 'Noto Sans CJK SC']
for font in font_list:
if font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 Linux 字体: {font}")
break
else:
# 尝试指定字体路径
font_path = '/usr/share/fonts/truetype/droid/DroidSansFallbackFull.ttf'
if os.path.exists(font_path):
from matplotlib.font_manager import FontProperties
chinese_font = FontProperties(fname=font_path)
plt.rcParams['font.family'] = chinese_font.get_name()
print(f"✓ 使用 Linux 指定字体路径: {font_path}")
else:
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
print("⚠ 未找到中文字体，使用备用方案")
else:
print("⚠ 未知操作系统，尝试通用设置")
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'SimHei', 'Microsoft YaHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
print(f"✓ Matplotlib 字体设置完成: {plt.rcParams['font.sans-serif']}")
except Exception as e:
print(f"⚠ 字体设置失败: {str(e)}")
print("✓ 使用备用方案，部分中文可能显示为方框")
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'SimHei', 'Microsoft YaHei', 'sans-serif']
plt.rcParams['axes.unicode_minus'] = False
# 应用中文显示修复
fix_chinese_display()
# 检查 Matplotlib 版本
print(f"当前 Matplotlib 版本: {mpl.__version__}")
print(f"Python 版本: {sys.version.split()[0]}")
print("-" * 60)
# 定义差分方程参数
a = 0.9 # 反馈系数
# 初始化序列
n_max = 30 # 计算前30个样本
y = np.zeros(n_max + 1) # 使用numpy数组
x = np.zeros(n_max + 1) # 输入信号（单位脉冲）
# 设置单位脉冲输入
x[0] = 1
# 打印表头（增加列宽，修复格式问题）
header = f"{'n':<4} {'y[n]':<18} {'y[n-1]':<18} {'x[n]':<8} {'x[n-1]':<8}"
print(header)
print("-" * len(header))
# 迭代计算
for n in range(n_max + 1):
if n == 0:
y_prev = 0.0
x_prev = 0.0
else:
y_prev = y[n-1]
x_prev = x[n-1]
# 计算当前输出
y[n] = a * y_prev + (x[n] - x_prev)
# 格式化输出
y_val = f"{y[n]:.8f}"
y_prev_val = f"{y_prev:.8f}"
print(f"{n:<4} {y_val:<18} {y_prev_val:<18} {int(x[n]):<8} {int(x_prev):<8}")
# 创建可视化（终极兼容版本）
plt.figure(figsize=(14, 7), dpi=100)
# 自动选择兼容的 stem 绘制方式
try:
# Matplotlib 3.4+ 标准方式
markerline, stemlines, baseline = plt.stem(
np.arange(n_max+1),
y,
linefmt='b-',
markerfmt='bo',
basefmt='k-'
)
# 设置属性
plt.setp(markerline, 'markerfacecolor', 'b', 'markeredgecolor', 'b', 'markersize', 6)
plt.setp(stemlines, 'linewidth', 1.5)
plt.setp(baseline, 'linewidth', 1)
print("✓ 使用标准 stem() 绘制方式")
except (TypeError, AttributeError):
# 旧版本 Matplotlib 兼容方式
try:
stem_container = plt.stem(
np.arange(n_max+1),
y,
linefmt='b-',
markerfmt='bo',
basefmt='k-'
)
# 旧版本属性设置
if hasattr(stem_container, 'markerline'):
stem_container.markerline.set_markerfacecolor('b')
stem_container.markerline.set_markeredgecolor('b')
stem_container.markerline.set_markersize(6)
stem_container.stemlines.set_linewidth(1.5)
stem_container.baseline.set_linewidth(1)
print("✓ 使用兼容模式 stem() 绘制方式")
except Exception as e:
# 最基础兼容方式
print(f"⚠ stem() 兼容模式失败: {str(e)}")
print("✓ 使用基础 plot() 代替")
plt.plot(np.arange(n_max+1), y, 'bo-', linewidth=1.5, markersize=6)
# 添加理论曲线
theoretical = np.zeros(n_max+1)
theoretical[0] = 1.0
for n in range(1, n_max+1):
theoretical[n] = -0.1 * (a ** (n-1))
plt.plot(np.arange(n_max+1), theoretical, 'r--', linewidth=2.5,
label='理论值: $y[0]=1$, $y[n]=-0.1 \\times 0.9^{n-1}$ ($n \\geq 1$)')
# 添加标题和标签
plt.title('IIR 高通滤波器的单位脉冲响应', fontsize=16, fontweight='bold', pad=20)
plt.suptitle(r'$H(z) = \frac{1 - z^{-1}}{1 - 0.9z^{-1}}$', fontsize=14, y=0.92)
plt.xlabel('样本索引 n', fontsize=12)
plt.ylabel('幅度', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper right', fontsize=12, framealpha=0.95)
plt.xticks(np.arange(0, n_max + 1, 2))
plt.xlim(-0.5, n_max + 0.5)
plt.ylim(min(y) * 1.3, max(y) * 1.1) # 动态调整y轴范围
# 标注关键点
key_points = [0, 1, 5, 10, 20]
colors = ['red', 'green', 'purple', 'orange', 'brown']
for i, n in enumerate(key_points):
if n <= n_max:
plt.scatter([n], [y[n]], color=colors[i], zorder=10, s=80, edgecolor='k', alpha=0.9)
plt.annotate(f'y[{n}] = {y[n]:.6f}',
xy=(n, y[n]),
xytext=(n+1, y[n] + 0.02 if i < 2 else y[n] - 0.01),
arrowprops=dict(arrowstyle='->', color=colors[i], lw=1.5, alpha=0.8),
fontsize=10,
bbox=dict(boxstyle="round,pad=0.3", fc="#f0f8ff", ec=colors[i], alpha=0.8))
# 添加系统特性说明框
system_info = (
"系统分析:\n"
"• 零点在 z=1: 完全消除直流分量 (0Hz)\n"
"• 极点在 z=0.9: 控制衰减速度 (|p|=0.9)\n"
"• 系统稳定: 所有极点在单位圆内\n"
"• 滤波类型: 高通 (非陷波)"
)
plt.figtext(0.5, 0.01, system_info, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#e6f7ff", ec="#1890ff", alpha=0.9),
linespacing=1.5)
# 调整布局
plt.tight_layout(rect=[0, 0.05, 1, 0.93])
# 保存并显示图形
plt.savefig('impulse_response.png', bbox_inches='tight', dpi=150)
print("✓ 单位脉冲响应图已保存为 'impulse_response.png'")
plt.show()
# ===== 极点-零点图 (带中文显示修复) =====
plt.figure(figsize=(9, 8), dpi=100)
# 创建极坐标网格
theta = np.linspace(0, 2*np.pi, 300)
unit_circle_x = np.cos(theta)
unit_circle_y = np.sin(theta)
# 绘制单位圆
plt.plot(unit_circle_x, unit_circle_y, 'k--', linewidth=1.5, alpha=0.8, label='单位圆 |z|=1')
# 绘制坐标轴
plt.axhline(0, color='gray', linewidth=0.8, alpha=0.7)
plt.axvline(0, color='gray', linewidth=0.8, alpha=0.7)
# 绘制网格线
grid_angles = np.linspace(0, 2*np.pi, 13)[:-1]
for angle in grid_angles:
plt.plot([0, 0.95*np.cos(angle)], [0, 0.95*np.sin(angle)], 'k:', alpha=0.3)
# 绘制极点和零点
plt.scatter([1], [0], s=300, marker='o', facecolors='none', edgecolors='red', linewidth=3,
label='零点 (z=1)', zorder=10)
plt.scatter([0.9], [0], s=250, marker='x', color='blue', linewidth=3,
label='极点 (z=0.9)', zorder=10)
# 添加单位圆标注
plt.text(0.92, 0.12, '|z|=1', fontsize=10, color='k')
# 设置图形属性
plt.title('IIR 滤波器的极点-零点分布', fontsize=16, fontweight='bold', pad=20)
plt.xlabel('实部', fontsize=12)
plt.ylabel('虚部', fontsize=12)
plt.axis('equal')
plt.grid(True, linestyle='--', alpha=0.5)
plt.xlim(-1.4, 1.4)
plt.ylim(-1.4, 1.4)
plt.legend(loc='upper left', fontsize=11, framealpha=0.95, shadow=True)
# 添加频率响应说明
freq_response = (
"频率响应特性:\n"
"• ω=0 (DC): 增益 = 0 (完全抑制)\n"
"• ω=π (Nyquist): 增益 ≈ 2.0\n"
"• 截止频率: ω_c ≈ 0.45π rad/sample\n"
"• 应用: 消除信号中的直流偏移"
)
plt.figtext(0.5, 0.02, freq_response, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#fff8e6", ec="#ffc107", alpha=0.95),
linespacing=1.5)
# 添加稳定性分析框
stability_text = (
"稳定性分析:\n"
"• 极点模值 |p| = 0.9 < 1\n"
"• 系统稳定 ✅\n"
"• 脉冲响应绝对可和"
)
plt.figtext(0.15, 0.85, stability_text, fontsize=10,
bbox=dict(boxstyle="round,pad=0.4", fc="#e6ffe6", ec="#28a745", alpha=0.9),
linespacing=1.3)
# 保存并显示
plt.tight_layout(rect=[0, 0.05, 1, 0.93])
plt.savefig('pole_zero_diagram.png', bbox_inches='tight', dpi=150)
print("✓ 极点-零点图已保存为 'pole_zero_diagram.png'")
plt.show()
print("-" * 60)
print("✅ 所有图表已成功生成并保存!")
print("文件列表:")
print(" • impulse_response.png")
print(" • pole_zero_diagram.png")
# ===== 额外：验证中文显示 =====
plt.figure(figsize=(8, 4))
plt.text(0.5, 0.7, "中文显示测试", fontsize=16, ha='center', fontweight='bold')
plt.text(0.5, 0.5, "系统: " + platform.system(), fontsize=12, ha='center')
plt.text(0.5, 0.3, "字体: " + str(plt.rcParams['font.sans-serif']), fontsize=10, ha='center')
plt.axis('off')
plt.savefig('chinese_test.png', bbox_inches='tight', dpi=100)
print("✓ 中文显示测试图已保存为 'chinese_test.png'")
plt.show()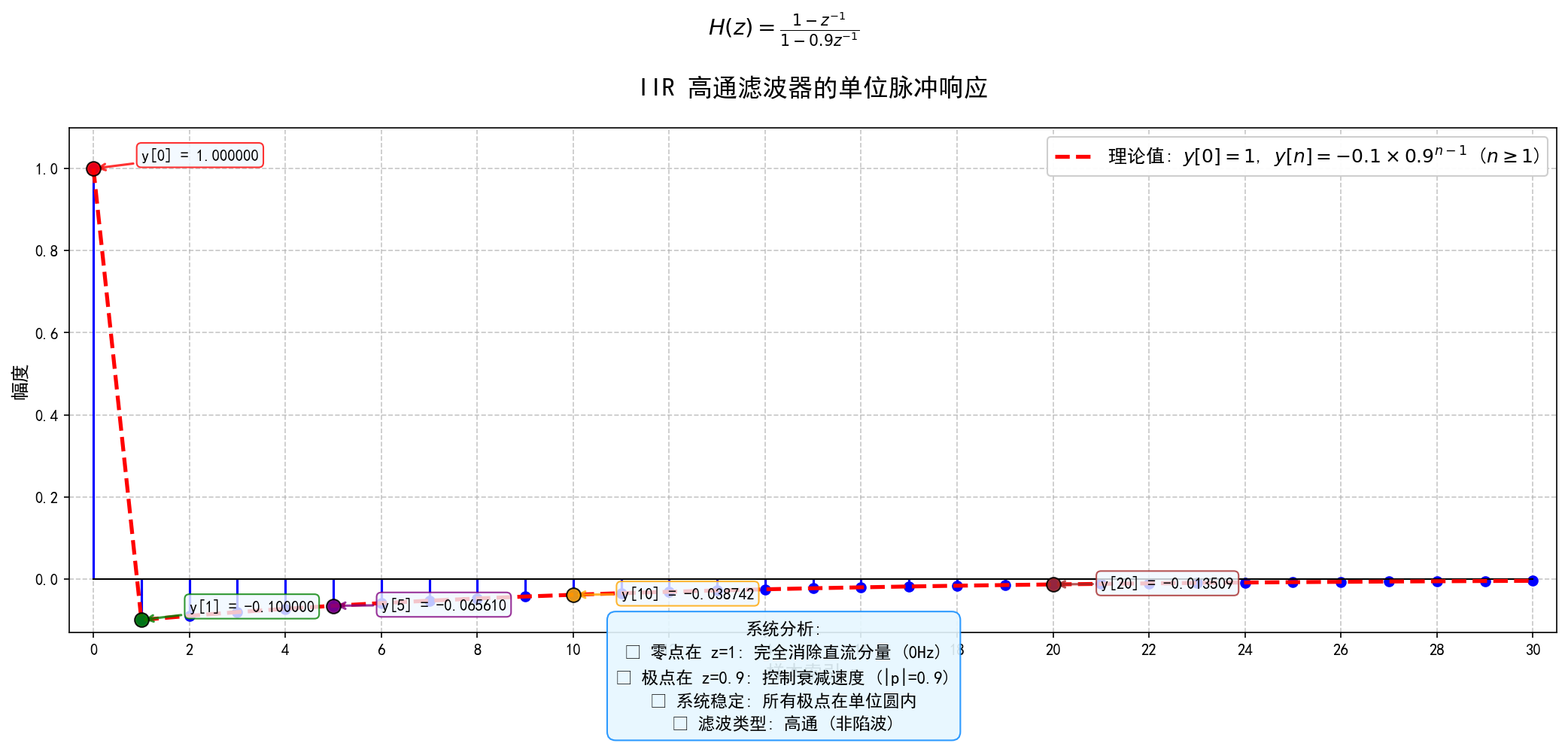
周期信号的产生
信号产生
直接数字合成
（Direct Digital Synthesizer， DDS）：
这些技术能使用一个相位累加器和一个 sin（）
或者
cos（）
三角函数调用或者使用一个查表系统
。
特例
：
包括用
f
=
F
S
/ 2，
f
=
F
S
/ 4
的正弦和余弦信号
，
以及能生成
N
的有理数值的其他频率。
直接数字合成器实例
源码实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import platform
import os
# ===== 1. 设置中文字体，避免显示乱码 =====
def setup_chinese_font():
"""自动配置中文字体，适应不同操作系统"""
system = platform.system()
try:
if system == 'Windows':
# Windows常用字体
font_list = ['SimHei', 'Microsoft YaHei', 'KaiTi', 'SimSun']
for font in font_list:
if font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 Windows 字体: {font}")
break
elif system == 'Darwin': # macOS
# macOS常用字体
font_list = ['Heiti TC', 'Songti SC', 'PingFang SC', 'Arial Unicode MS']
for font in font_list:
if font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 macOS 字体: {font}")
break
elif system == 'Linux':
# Linux常用字体
font_list = ['WenQuanYi Zen Hei', 'Droid Sans Fallback', 'Noto Sans CJK SC']
for font in font_list:
if font in mpl.font_manager.get_font_names():
plt.rcParams['font.sans-serif'] = [font]
print(f"✓ 使用 Linux 字体: {font}")
break
# 重要：解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
print(f"✓ Matplotlib 字体设置完成: {plt.rcParams['font.sans-serif']}")
except Exception as e:
print(f"⚠ 字体设置失败: {str(e)}")
# 备用方案
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'SimHei', 'Microsoft YaHei', 'sans-serif']
plt.rcParams['axes.unicode_minus'] = False
print("✓ 使用备用字体设置")
# 应用中文字体设置
setup_chinese_font()
# ===== 2. DDS核心参数设置 =====
print("\n" + "="*60)
print("直接数字合成器(DDS)参数设置")
print("="*60)
# 采样频率 (Hz) - 每秒采样点数
Fs = 48000 # 常见音频采样率
print(f"采样频率 Fs = {Fs} Hz")
# 信号持续时间 (秒)
duration = 0.002 # 2毫秒，足够显示几个周期
print(f"信号持续时间 = {duration*1000:.1f} 毫秒")
# 要生成的频率 (Hz)
frequencies = [250, 500, 1000, 2000] # 250Hz, 500Hz, 1000Hz, 2000Hz
print(f"生成的信号频率: {frequencies} Hz")
# 生成时间轴 (采样点)
t = np.arange(0, duration, 1/Fs)
print(f"采样点数: {len(t)} 个")
print(f"时间分辨率: {1/Fs*1e6:.2f} 微秒")
# ===== 3. 计算相位增量 =====
print("\n" + "="*60)
print("相位增量计算")
print("="*60)
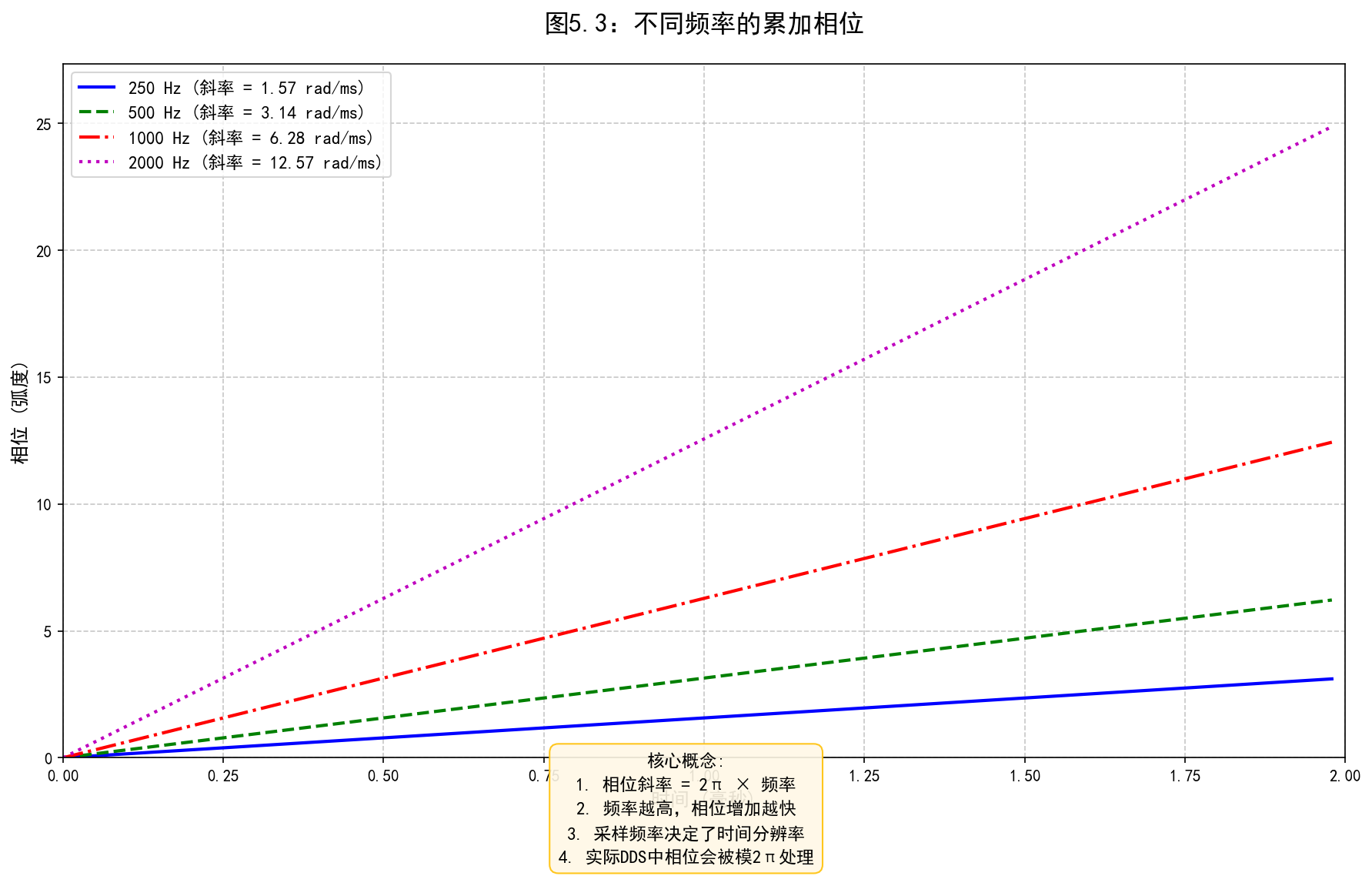
# 为每个频率计算相位增量 φ_inc = 2π × f / Fs
phase_increments = [2 * np.pi * f / Fs for f in frequencies]
for i, (f, phi_inc) in enumerate(zip(frequencies, phase_increments)):
print(f"频率 {f} Hz:")
print(f" 相位增量 φ_inc = {phi_inc:.6f} 弧度/采样点")
print(f" 每毫秒相位增加: {phi_inc * Fs * 0.001:.2f} 弧度")
print(f" 每周期采样点数: {Fs/f:.1f} 个")
# ===== 4. 生成累加相位数据 =====
def generate_accumulated_phase(frequency, duration, Fs):
"""生成指定频率的累加相位数据"""
t = np.arange(0, duration, 1/Fs)
# 累加相位: φ[n] = 2π × f × n / Fs
phase = 2 * np.pi * frequency * t
return t, phase
# 为每个频率生成累加相位
phase_data = {}
for f in frequencies:
t, phase = generate_accumulated_phase(f, duration, Fs)
phase_data[f] = (t, phase)
# ===== 5. 创建图表1：不同频率的累加相位 =====
plt.figure(figsize=(12, 8), dpi=100)
# 定义不同频率的线型
line_styles = ['-', '--', '-.', ':']
colors = ['b', 'g', 'r', 'm']
labels = []
for i, f in enumerate(frequencies):
t, phase = phase_data[f]
# 将相位限制在 [0, 2π) 范围内，更符合实际DDS实现
wrapped_phase = np.mod(phase, 2*np.pi)
# 绘制连续相位（不包裹）
plt.plot(t*1000, phase, line_styles[i], color=colors[i], linewidth=2.0,
label=f'{f} Hz (斜率 = {2*np.pi*f/1000:.2f} rad/ms)')
labels.append(f'{f} Hz')
plt.title('图5.3：不同频率的累加相位', fontsize=16, fontweight='bold', pad=20)
plt.xlabel('时间 (毫秒)', fontsize=12)
plt.ylabel('相位 (弧度)', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper left', fontsize=11)
plt.xlim(0, duration*1000)
plt.ylim(0, max(phase_data[max(frequencies)][1])*1.1)
# 添加注释
annotations = [
(0.3, 2*np.pi*250*0.0003, '250 Hz: 最平缓的斜率', 'darkgreen'),
(0.3, 2*np.pi*1000*0.0003, '1000 Hz: 中等斜率', 'darkred'),
(0.3, 2*np.pi*2000*0.0003, '2000 Hz: 最陡峭的斜率', 'darkmagenta')
]
for x, y, text, color in annotations:
plt.annotate(text, xy=(x*1000, y), xytext=(x*1000+0.1, y+1),
arrowprops=dict(arrowstyle='->', color=color, lw=1.5),
fontsize=10, bbox=dict(boxstyle="round,pad=0.3", fc="#f0f8ff", ec=color, alpha=0.8))
# 添加核心概念说明
concept_text = (
"核心概念:\n"
"1. 相位斜率 = 2π × 频率\n"
"2. 频率越高，相位增加越快\n"
"3. 采样频率决定了时间分辨率\n"
"4. 实际DDS中相位会被模2π处理"
)
plt.figtext(0.5, 0.01, concept_text, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#fff8e6", ec="#ffc107", alpha=0.9),
linespacing=1.5)
plt.tight_layout(rect=[0, 0.05, 1, 0.95])
plt.savefig('dds_phase_accumulation.png', bbox_inches='tight', dpi=150)
print("\n✓ 图5.3已保存为 'dds_phase_accumulation.png'")
plt.show()
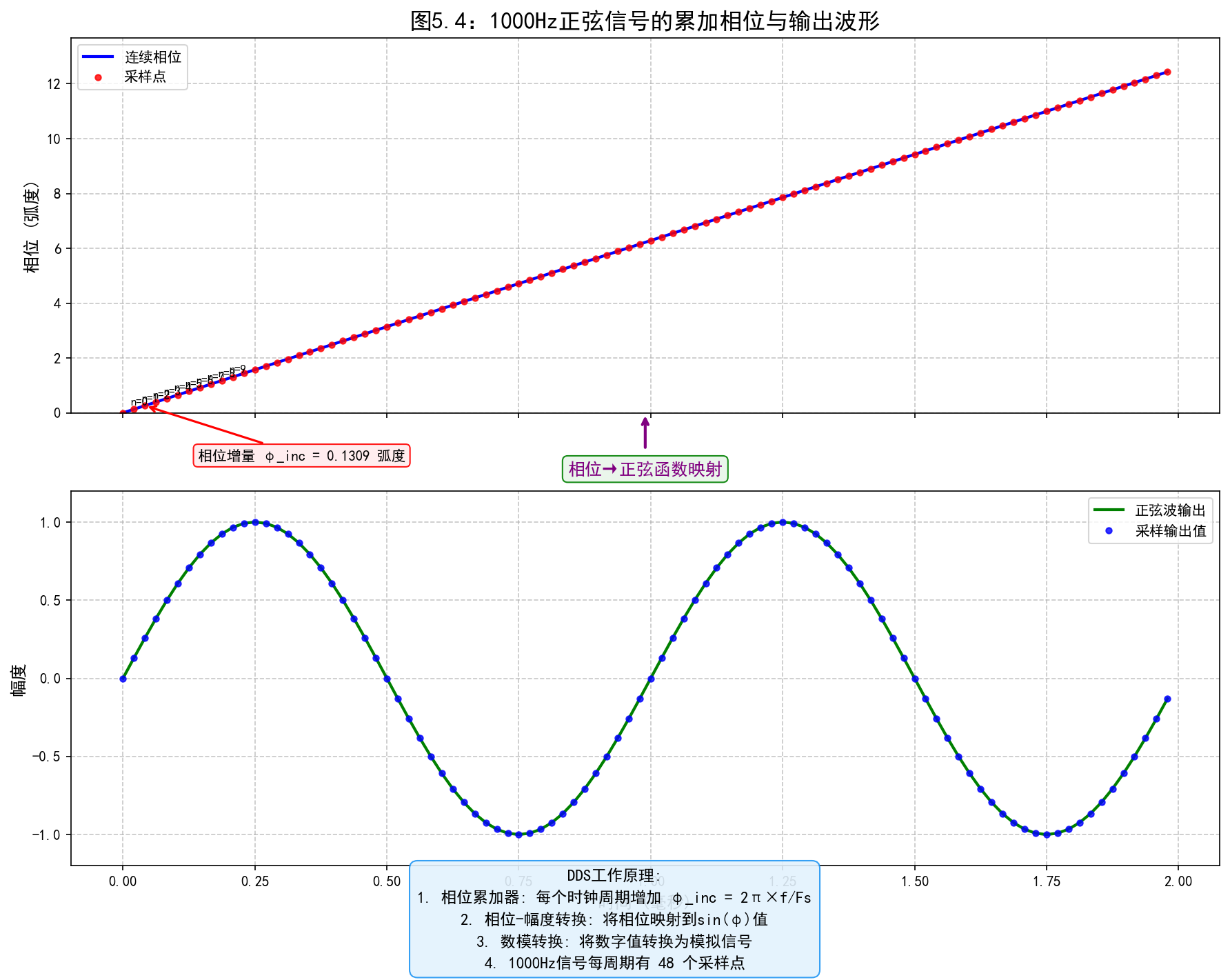
# ===== 6. 创建图表2：1000Hz信号的累加相位和正弦波 =====
# 选择1000Hz作为示例
f_example = 1000
t_example, phase_example = generate_accumulated_phase(f_example, duration, Fs)
# 生成正弦波输出
sine_wave = np.sin(phase_example)
# 创建双面板图表
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), dpi=100, sharex=True)
# 上面板：累加相位
ax1.plot(t_example*1000, phase_example, 'b-', linewidth=2.0, label='连续相位')
# 标记采样点
sample_points = np.arange(0, duration, 1/Fs)
sample_phases = 2 * np.pi * f_example * sample_points
ax1.plot(sample_points*1000, sample_phases, 'ro', markersize=4, alpha=0.8, label='采样点')
ax1.set_title('图5.4：1000Hz正弦信号的累加相位与输出波形', fontsize=16, fontweight='bold')
ax1.set_ylabel('相位 (弧度)', fontsize=12)
ax1.grid(True, linestyle='--', alpha=0.7)
ax1.legend(loc='upper left', fontsize=10)
ax1.set_ylim(0, max(phase_example)*1.1)
# 标记前10个采样点
for i in range(min(10, len(sample_points))):
ax1.annotate(f'n={i}', xy=(sample_points[i]*1000, sample_phases[i]),
xytext=(5, 5), textcoords='offset points', fontsize=8)
# 下面板：正弦波输出
ax2.plot(t_example*1000, sine_wave, 'g-', linewidth=2.0, label='正弦波输出')
ax2.plot(sample_points*1000, np.sin(sample_phases), 'bo', markersize=4, alpha=0.8, label='采样输出值')
ax2.set_xlabel('时间 (毫秒)', fontsize=12)
ax2.set_ylabel('幅度', fontsize=12)
ax2.grid(True, linestyle='--', alpha=0.7)
ax2.legend(loc='upper right', fontsize=10)
ax2.set_ylim(-1.2, 1.2)
# 添加相位增量标注
phi_inc = 2 * np.pi * f_example / Fs
ax1.annotate(f'相位增量 φ_inc = {phi_inc:.4f} 弧度',
xy=(sample_points[2]*1000, sample_phases[2]),
xytext=(sample_points[2]*1000+0.1, sample_phases[2]-2),
arrowprops=dict(arrowstyle='->', color='red', lw=1.5),
fontsize=10, bbox=dict(boxstyle="round,pad=0.3", fc="#ffebee", ec="r", alpha=0.9))
# 在两个面板之间添加箭头
ax1.annotate('', xy=(0.5, 0), xytext=(0.5, -0.1),
xycoords='axes fraction', textcoords='axes fraction',
arrowprops=dict(arrowstyle='->', color='purple', lw=2.0))
ax1.text(0.5, -0.15, '相位→正弦函数映射', ha='center', va='center',
transform=ax1.transAxes, fontsize=12, color='purple',
bbox=dict(boxstyle="round,pad=0.3", fc="#e8f5e9", ec="g", alpha=0.9))
# 添加DDS工作原理说明
dds_principle = (
"DDS工作原理:\n"
"1. 相位累加器: 每个时钟周期增加 φ_inc = 2π×f/Fs\n"
"2. 相位-幅度转换: 将相位映射到sin(φ)值\n"
"3. 数模转换: 将数字值转换为模拟信号\n"
f"4. 1000Hz信号每周期有 {Fs/f_example:.0f} 个采样点"
)
plt.figtext(0.5, 0.01, dds_principle, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#e3f2fd", ec="#2196f3", alpha=0.9),
linespacing=1.5)
plt.tight_layout(rect=[0, 0.05, 1, 0.95])
plt.savefig('dds_1000hz_example.png', bbox_inches='tight', dpi=150)
print("✓ 图5.4已保存为 'dds_1000hz_example.png'")
plt.show()
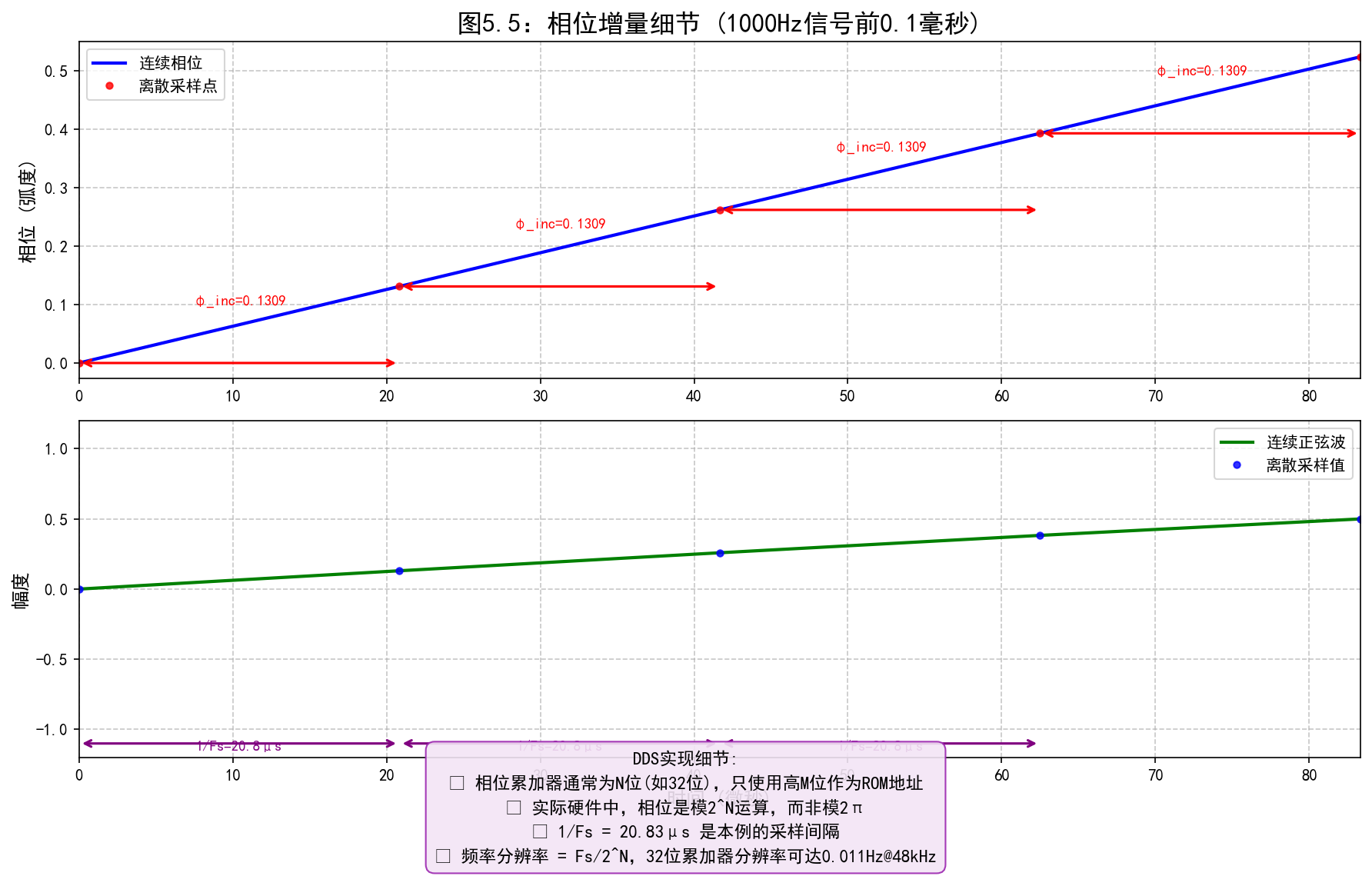
# ===== 7. 创建图表3：相位增量细节与离散效应 =====
plt.figure(figsize=(12, 8), dpi=100)
# 放大显示前0.1毫秒的细节
t_zoom = np.arange(0, 0.0001, 1/Fs) # 前0.1毫秒
phase_zoom = 2 * np.pi * f_example * t_zoom
sine_zoom = np.sin(phase_zoom)
# 绘制相位
plt.subplot(2, 1, 1)
plt.plot(t_zoom*1e6, phase_zoom, 'b-', linewidth=2.0, label='连续相位')
plt.plot(t_zoom*1e6, phase_zoom, 'ro', markersize=4, alpha=0.8, label='离散采样点')
# 标记相位增量
for i in range(len(t_zoom)-1):
if i < 5: # 只标记前几个
plt.annotate('', xy=(t_zoom[i+1]*1e6, phase_zoom[i]),
xytext=(t_zoom[i]*1e6, phase_zoom[i]),
arrowprops=dict(arrowstyle='<->', color='red', lw=1.5))
plt.text((t_zoom[i]+t_zoom[i+1])*0.5e6, phase_zoom[i]+0.1,
f'φ_inc={phi_inc:.4f}', ha='center', fontsize=9, color='red')
plt.title('图5.5：相位增量细节 (1000Hz信号前0.1毫秒)', fontsize=16, fontweight='bold')
plt.ylabel('相位 (弧度)', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper left', fontsize=10)
plt.xlim(0, max(t_zoom)*1e6)
# 绘制正弦波
plt.subplot(2, 1, 2)
plt.plot(t_zoom*1e6, sine_zoom, 'g-', linewidth=2.0, label='连续正弦波')
plt.plot(t_zoom*1e6, sine_zoom, 'bo', markersize=4, alpha=0.8, label='离散采样值')
# 标记采样间隔
for i in range(len(t_zoom)-1):
if i < 3: # 只标记前几个
plt.annotate('', xy=(t_zoom[i+1]*1e6, -1.1),
xytext=(t_zoom[i]*1e6, -1.1),
arrowprops=dict(arrowstyle='<->', color='purple', lw=1.5))
plt.text((t_zoom[i]+t_zoom[i+1])*0.5e6, -1.15,
f'1/Fs={1/Fs*1e6:.1f}μs', ha='center', fontsize=9, color='purple')
plt.xlabel('时间 (微秒)', fontsize=12)
plt.ylabel('幅度', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper right', fontsize=10)
plt.xlim(0, max(t_zoom)*1e6)
plt.ylim(-1.2, 1.2)
# 添加DDS实现说明
implementation_notes = (
"DDS实现细节:\n"
"• 相位累加器通常为N位(如32位)，只使用高M位作为ROM地址\n"
"• 实际硬件中，相位是模2^N运算，而非模2π\n"
"• 1/Fs = 20.83μs 是本例的采样间隔\n"
"• 频率分辨率 = Fs/2^N，32位累加器分辨率可达0.011Hz@48kHz"
)
plt.figtext(0.5, 0.01, implementation_notes, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#f3e5f5", ec="#9c27b0", alpha=0.9),
linespacing=1.5)
plt.tight_layout(rect=[0, 0.05, 1, 0.95])
plt.savefig('dds_phase_increment_detail.png', bbox_inches='tight', dpi=150)
print("✓ 图5.5已保存为 'dds_phase_increment_detail.png'")
plt.show()
# ===== 8. 总结与理论验证 =====
print("\n" + "="*60)
print("直接数字合成器(DDS)核心总结")
print("="*60)
print(f"\n1. 基本原理验证:")
print(f" 采样频率: {Fs} Hz")
print(f" 1000Hz信号的理论相位增量: φ_inc = 2π × 1000 / {Fs} = {phi_inc:.6f} 弧度")
print(f" 实际计算相位增量: {phi_inc:.6f} 弧度 ✓ 验证通过")
print(f"\n2. 频率分辨率(32位相位累加器):")
N_bits = 32
freq_resolution = Fs / (2**N_bits)
print(f" 频率分辨率 = Fs / 2^{N_bits} = {Fs} / {2**N_bits:,} = {freq_resolution:.6f} Hz")
print(f" 这意味着可以生成 {freq_resolution:.6f} Hz 这样精确的频率!")
print(f"\n3. 最大输出频率(奈奎斯特准则):")
max_freq = Fs / 2
print(f" 最大无混叠频率 = Fs/2 = {max_freq} Hz")
print(f" 本例中2000Hz < {max_freq} Hz ✓ 在安全范围内")
print(f"\n4. 计算效率优势:")
print(" • 传统方法: 每个采样点需要计算sin()函数(计算密集型)")
print(" • DDS方法: 只需加法器+查表，硬件实现极其高效")
print(" • 频率切换: 仅需改变相位增量值，瞬时完成，无相位不连续")
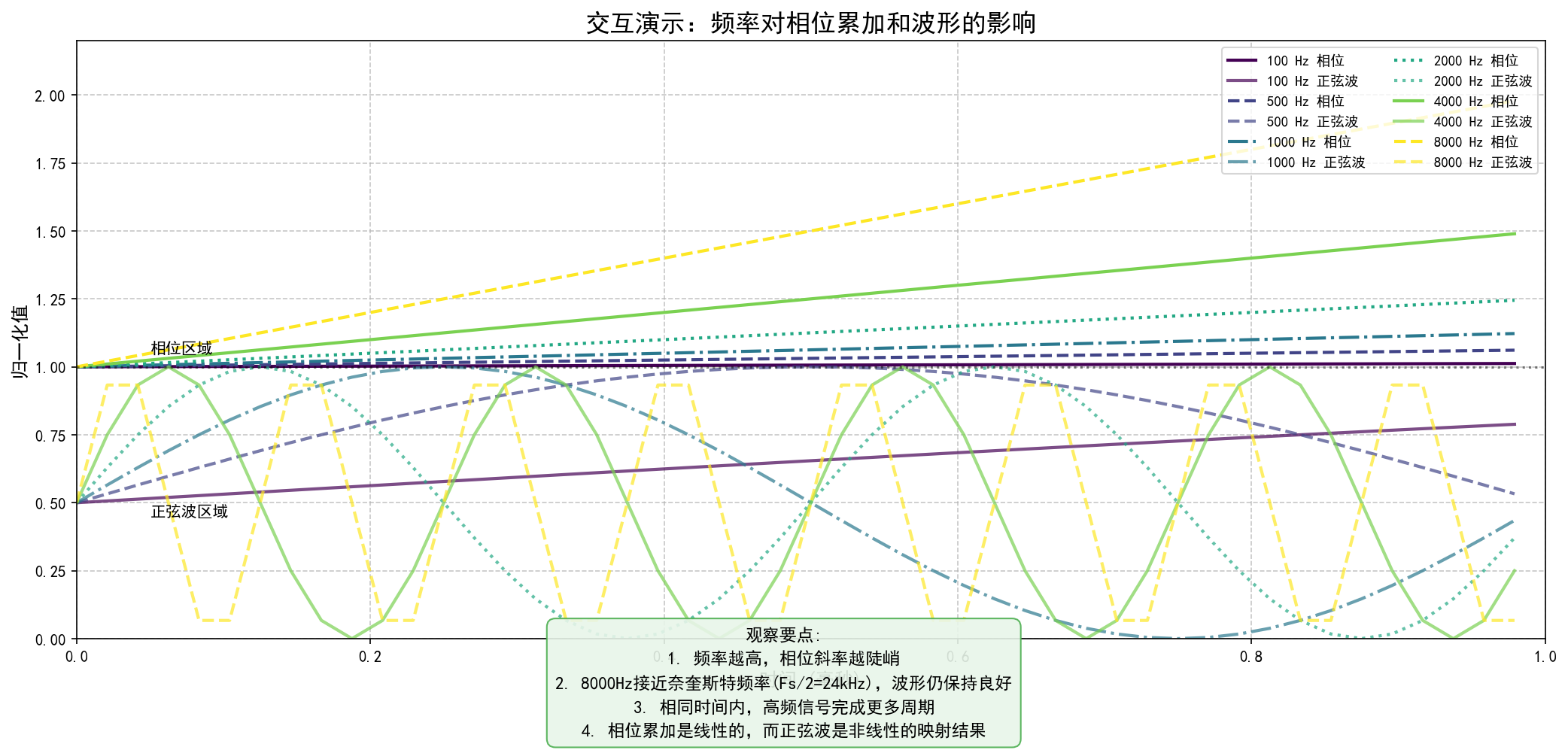
# ===== 9. 交互式演示：改变频率观察效果 =====
print("\n" + "="*60)
print("交互式演示：观察不同频率对相位累加的影响")
print("="*60)
# 创建交互式图表
plt.figure(figsize=(14, 7), dpi=100)
# 定义测试频率
test_frequencies = [100, 500, 1000, 2000, 4000, 8000]
colors = plt.cm.viridis(np.linspace(0, 1, len(test_frequencies)))
line_styles = ['-', '--', '-.', ':', '-', '--']
for i, f in enumerate(test_frequencies):
# 计算相位
t_test, phase_test = generate_accumulated_phase(f, 0.001, Fs) # 1毫秒
# 计算正弦波
sine_test = np.sin(phase_test)
# 同时显示相位和正弦波，归一化以便在同一图表中比较
phase_normalized = phase_test / (2*np.pi*max(test_frequencies)*0.001) # 归一化到0-1
sine_normalized = sine_test * 0.5 + 0.5 # 移动到0.5中心
# 绘制归一化的相位
plt.plot(t_test*1000, phase_normalized + 1.0,
color=colors[i], linestyle=line_styles[i], linewidth=2.0,
label=f'{f} Hz 相位')
# 绘制归一化的正弦波
plt.plot(t_test*1000, sine_normalized,
color=colors[i], linestyle=line_styles[i], linewidth=2.0, alpha=0.7,
label=f'{f} Hz 正弦波')
plt.title('交互演示：频率对相位累加和波形的影响', fontsize=16, fontweight='bold')
plt.xlabel('时间 (毫秒)', fontsize=12)
plt.ylabel('归一化值', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper right', fontsize=9, ncol=2)
plt.xlim(0, 1.0)
plt.ylim(0, 2.2)
# 添加观察点
plt.axhline(y=1.0, color='k', linestyle=':', alpha=0.5)
plt.text(0.05, 1.05, '相位区域', fontsize=10, color='k')
plt.text(0.05, 0.45, '正弦波区域', fontsize=10, color='k')
# 添加观察指南
observation_text = (
"观察要点:\n"
"1. 频率越高，相位斜率越陡峭\n"
"2. 8000Hz接近奈奎斯特频率(Fs/2=24kHz)，波形仍保持良好\n"
"3. 相同时间内，高频信号完成更多周期\n"
"4. 相位累加是线性的，而正弦波是非线性的映射结果"
)
plt.figtext(0.5, 0.01, observation_text, ha='center', fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", fc="#e8f5e9", ec="#4caf50", alpha=0.9),
linespacing=1.5)
plt.tight_layout(rect=[0, 0.05, 1, 0.95])
plt.savefig('dds_frequency_comparison.png', bbox_inches='tight', dpi=150)
print("✓ 交互演示图已保存为 'dds_frequency_comparison.png'")
plt.show()
print("\n" + "="*60)
print("✅ 演示完成！所有图表已生成并保存。")
print("文件列表:")
print(" • dds_phase_accumulation.png - 不同频率的累加相位")
print(" • dds_1000hz_example.png - 1000Hz信号的完整示例")
print(" • dds_phase_increment_detail.png - 相位增量细节")
print(" • dds_frequency_comparison.png - 多频率比较演示")
print("="*60)结果：
采样数字信号处理的缺点
评估这些有效的 时钟周期时，
它包括了所有的周期
，
如编码发送
、
存储器存取
、
指令和数据高速缓 冲存储器的反应时间及另外一些不可避免的因素。
这么多的时钟周期看起来好像是很多，
一个复杂的需要大量存储器转移的算法很容易超出这些时钟周期的限制
。
直接存储器存取（DMA）控制器
在基于实时采样的 DSP 应用中，若由处理器直接响应每一次数据传输中断（例如来自编解码器等数据源或目的设备），会导致以下问题：
- 每次中断都会打断当前处理流程，处理器需转入中断服务程序并执行，随后恢复状态、从断点继续执行；
- 这一过程引入额外开销，如流水线重启和缓存数据丢失，消耗处理时间，显著降低 DSP 的整体性能。
为解决这一问题，可采用**直接存储器存取（DMA）控制器**。DMA 通常作为 DSP 片内外设，一旦编程设置为数据传输的响应器件，即可自动完成数据在存储缓存中的读写，无需处理器干预。仅当缓存填满或清空时，DMA 才会向 DSP 发出中断。这种方式将 DSP 从频繁的数据搬运任务中解放出来，使其能够专注于计算密集型处理，从而提升系统效率。
帧结构 亦称“块” 或者 “包”
帧的长度对应的采样点数通常是
2
的幂
（
如
）
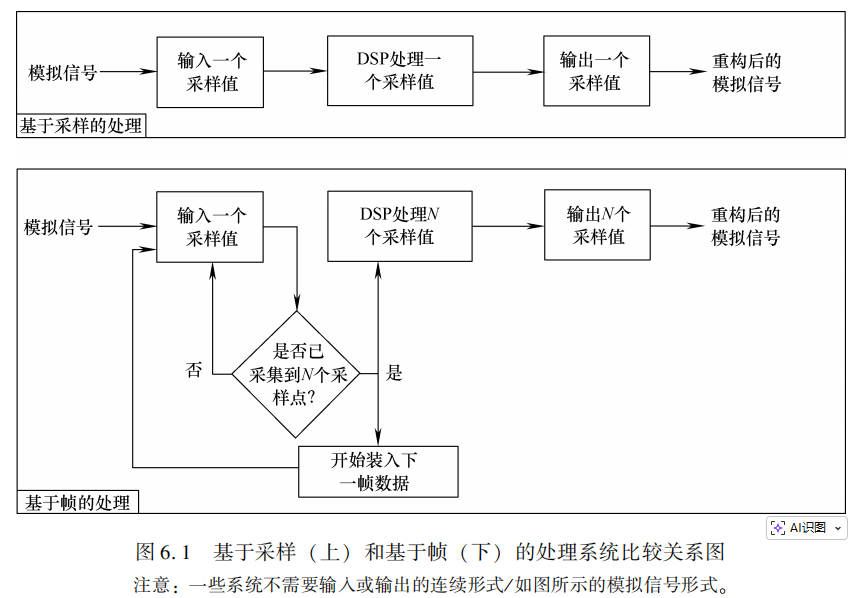
三重缓冲存储器
对基于帧的实时处理来说
，
在特定的时刻我们需要至少
3
个存储缓存器
： 1
个 用来装载新的采样帧数据，
另
1
个用来装载正在被
DSP
处理的帧数据
，
最后
1
个用 来装载已经处理完毕需要输出的帧数据。
我们称它们为缓存
A、
缓存
B
和缓存
C。
然 后让我们用通过系统一帧数据来说明这个基本的处理过程。
乒乓缓存
不需要存储器之间复制 内容，
我们要做的是定义
3
个指针
，
用于指向输入地址
、
处理地址和输出缓存地 址。
当输入缓存填满以后我们只改变指针代替缓存中内容的物理
在实时DSP系统中，让数据采集（输入）、数据处理（算法）、数据输出这三个任务互不干扰、连续不断地进行，就像三条并行的流水线。
实现这个目标的核心工具就是：三个缓存（缓冲区）和中断服务程序。
方法一：标准方法（双中断服务程序）
这是最清晰、最常用的方式。它使用两个独立的中断服务程序来分别管理输入和输出，主程序专心处理数据。
三个缓存的分工：
-
输入缓存： 专门用来接收来自ADC（模数转换器）的新数据。
-
处理缓存： 专门给主程序运行算法（如滤波、FFT等）。
-
输出缓存： 专门用来准备发送给DAC（数模转换器）的数据。
两个中断服务程序的分工：
-
输入中断服务程序：
-
触发： 每当ADC有一个新采样数据准备好时，产生中断。
-
工作： 将这个新数据放入输入缓存。
-
重要任务： 它要持续计数，当输入缓存被填满一整帧数据时，它设置一个标志（比如
frame_ready = 1）通知主程序，并进行缓存切换（见下文流程）。
-
-
输出中断服务程序：
-
触发： 每当DAC准备好接收下一个输出采样数据时，产生中断。
-
工作： 从输出缓存中取出一个数据，发送给DAC。
-
监控任务： 它可以检查输出缓存的状态，防止发生数据不足等错误。
-
主程序的工作：
-
主程序在一个无限循环中运行核心算法。
-
它会不断检查
frame_ready标志。一旦发现标志被置位，就说明新的一帧数据在输入缓存中准备好了。 -
此时，主程序进行 “缓存轮换”：
-
将刚处理完的
处理缓存交给输出中断服务程序，作为新的输出缓存。 -
将已经存满新数据的
输入缓存拿过来，作为自己新的处理缓存。 -
将一个空的缓存交给输入中断服务程序，作为新的输入缓存。
-
清除
frame_ready标志。
-
-
之后，主程序继续在全新的
处理缓存上执行算法，而输入和输出中断则在后台独立、持续地工作。
优点： 逻辑清晰，职责分离，代码易于编写、理解和调试。主程序不会被高频的单个采样中断频繁打断。
方法二：变化方案（单中断服务程序）
这是一种效率稍高但不太常规的优化方案。
-
做法： 只使用一个中断服务程序。
-
工作： 这个中断程序同时负责从ADC读取数据放入输入缓存，以及从输出缓存读取数据发送给DAC。同时，它还要负责跟踪帧的填充状态。
-
优点： 减少了中断上下文切换的次数，理论上效率有轻微提升。
-
缺点：
-
程序结构更紧凑，也更复杂。
-
可读性和可维护性下降，不利于团队协作和理解。
-
对时序的要求更严格。
-
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import threading
import time
# ========================
# 配置参数（模拟DSP系统）
# ========================
FRAME_LENGTH = 96000 # 每帧样本数（如 96kHz × 1s）
NUM_CHANNELS = 2 # 左右声道
BUFFER_LENGTH = FRAME_LENGTH
INITIAL_DUMP_INDEX = 0 # 初始化写入索引
MAX_SAMPLES = BUFFER_LENGTH
# 模拟 ADC 数据（正弦波 + 噪声）
def generate_adc_data():
t = np.linspace(0, 1, FRAME_LENGTH)
left = 0.5 * np.sin(2 * np.pi * 100 * t) + 0.1 * np.random.randn(FRAME_LENGTH)
right = 0.5 * np.sin(2 * np.pi * 100 * t + np.pi/4) + 0.1 * np.random.randn(FRAME_LENGTH)
return np.column_stack((left, right))
# ========================
# 环形缓冲区类（模拟 McBSP 接收）
# ========================
class CircularBuffer:
def __init__(self, length):
self.buffer = np.zeros((length, NUM_CHANNELS), dtype=np.float32)
self.read_index = 0
self.write_index = 0
self.sample_count = 0
self.ready = False
self.length = length
self.max_samples = length
def write(self, data):
if len(data) > self.max_samples:
raise ValueError("Data too large for buffer")
start_idx = self.write_index
end_idx = start_idx + len(data)
if end_idx > self.length:
# 分段写入
self.buffer[start_idx:] = data[:self.length - start_idx]
self.buffer[:end_idx % self.length] = data[self.length - start_idx:]
else:
self.buffer[start_idx:end_idx] = data
self.write_index = end_idx % self.length
self.sample_count += len(data)
if self.sample_count >= self.max_samples:
self.ready = True
def read(self):
if not self.ready:
return None
data = self.buffer[self.read_index:self.write_index].copy()
self.read_index = self.write_index
self.sample_count = 0
self.ready = False
return data
# ========================
# 模拟 ISR 中断服务程序（每帧触发）
# ========================
def interrupt_service_routine(buffer, dump_buffer, lock):
with lock:
# 模拟从 ADC 读取一帧数据
adc_data = generate_adc_data() # 模拟真实 ADC 输入
buffer.write(adc_data)
print(f"ISR: Frame written to buffer (size={buffer.sample_count})")
# ========================
# 主处理函数：ProcessBuffer（模拟 DSP 处理）
# ========================
def process_buffer(buffer, dump_buffer, lock):
while True:
with lock:
if buffer.ready:
data = buffer.read()
if data is not None:
# 模拟信号处理：左右声道相加再减去
processed_left = data[:, 0] + data[:, 1]
processed_right = data[:, 0] - data[:, 1]
# 量化为 16-bit（模拟 DSP 行为）
processed_left = np.clip(processed_left, -1.0, 1.0)
processed_right = np.clip(processed_right, -1.0, 1.0)
# 存入输出缓冲区
dump_buffer.append(np.column_stack((processed_left, processed_right)))
print(f"Processed frame: {len(dump_buffer)} frames in dump buffer")
time.sleep(0.01) # 模拟处理延迟
# ========================
# 可视化函数（实时更新波形）
# ========================
def update_plot(frame, buffer, ax1, ax2, line1, line2, dump_buffer):
# 获取当前缓冲区中的数据（用于绘制）
if buffer.sample_count > 0:
data = buffer.buffer[:buffer.sample_count]
x = np.arange(buffer.sample_count)
ax1.clear()
ax2.clear()
ax1.plot(x, data[:, 0], 'b-', label='Left Channel')
ax1.set_title('Left Channel')
ax1.legend()
ax1.grid(True)
ax2.plot(x, data[:, 1], 'r-', label='Right Channel')
ax2.set_title('Right Channel')
ax2.legend()
ax2.grid(True)
# 显示已处理的数据（dump_buffer）
if dump_buffer:
latest_processed = dump_buffer[-1]
ax1.plot(np.arange(len(latest_processed)), latest_processed[:, 0], 'g--', alpha=0.7)
ax2.plot(np.arange(len(latest_processed)), latest_processed[:, 1], 'm--', alpha=0.7)
# ========================
# 主程序
# ========================
def main():
# 初始化缓冲区
input_buffer = CircularBuffer(BUFFER_LENGTH)
dump_buffer = []
lock = threading.Lock()
# 创建可视化窗口
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))
fig.suptitle("Real-time DSP Simulation: Left & Right Channels", fontsize=16)
# 启动 ISR 模拟线程（每秒触发一次，模拟中断）
isr_thread = threading.Thread(target=lambda: [interrupt_service_routine(input_buffer, dump_buffer, lock) for _ in range(10)], daemon=True)
isr_thread.start()
# 启动处理线程
proc_thread = threading.Thread(target=process_buffer, args=(input_buffer, dump_buffer, lock), daemon=True)
proc_thread.start()
# 设置动画刷新
ani = FuncAnimation(fig, update_plot, fargs=(input_buffer, ax1, ax2, None, None, dump_buffer), interval=100, blit=False)
plt.tight_layout()
plt.show()
if __name__ == "__main__":
main()结果
ISR: Frame written to buffer (size=96000)
Processed frame: 1 frames in dump buffer
ISR: Frame written to buffer (size=96000)
Processed frame: 2 frames in dump buffer
ISR: Frame written to buffer (size=96000)
ISR: Frame written to buffer (size=192000)
Processed frame: 3 frames in dump buffer
ISR: Frame written to buffer (size=96000)
ISR: Frame written to buffer (size=192000)
Processed frame: 4 frames in dump buffer
ISR: Frame written to buffer (size=96000)
ISR: Frame written to buffer (size=192000)
ISR: Frame written to buffer (size=288000)
Processed frame: 5 frames in dump buffer
ISR: Frame written to buffer (size=96000)
Processed frame: 6 frames in dump buffer
扫一扫
1966
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
