理解 FIR 对帧的处理
卷积和成为了 FIR 差分等式的一般形式为
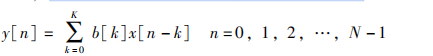
为计算出一个完整帧的滤波器的输出值, 我们需要 “滑动” 这个滤波器的系数 “越过” 滤波器输入的整个帧, 如上述等式指出的那样, 进行点对点的相乘并求和。
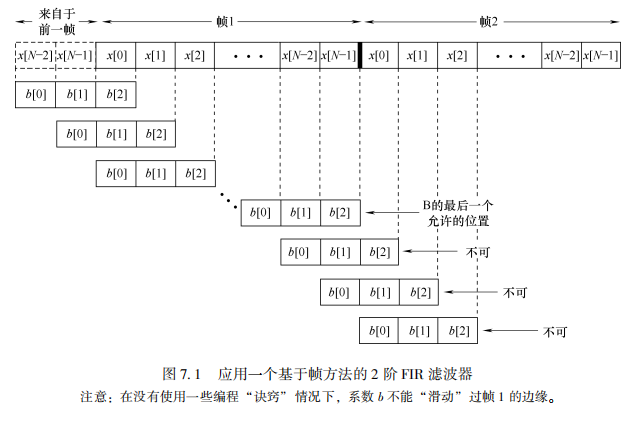
利用 “历史缓冲区” 来解决分帧处理时的边缘效应
核心策略
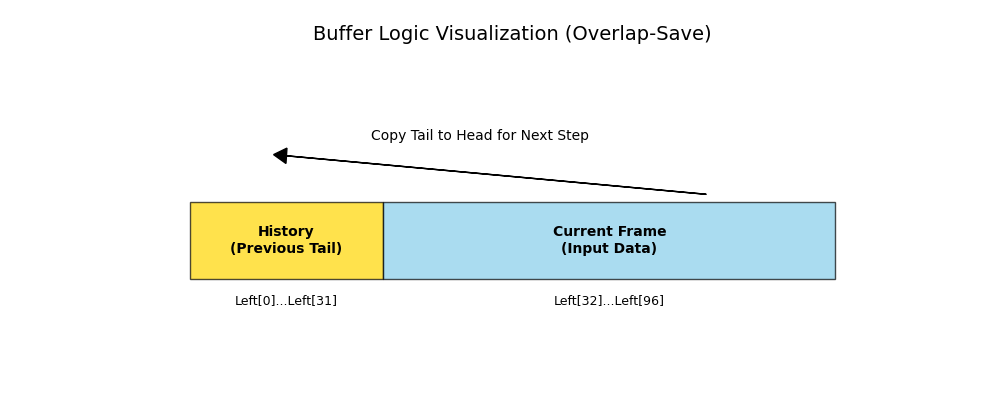
通过扩大缓存空间来实现数据的逻辑连续性,即:“用上一帧的尾巴,补当前帧的头”。
具体步骤
-
建立大缓存: 创建一个足够大的矩阵(缓冲区),其容量 = 保持区域(上一帧的边缘值) + 当前帧(帧 1)的数据。
-
跨边界处理: 滤波器不只处理当前帧,而是从“保持区域”的最左侧开始滑动,横跨历史数据和当前帧,直到当前帧末尾。这保证了当前帧的开头拥有完整的上下文数据。
-
数据搬运(关键点): 在下一帧(帧 2)进入并覆盖当前数据之前,将 帧 1 最右侧(末尾) 的数据复制并存储到 “保持区域”。
结果
通过这种“复制-存储”机制,每一帧数据在处理时都能获取到所需的历史值,从而消除了因分块处理导致的边缘断裂或失真问题。这在 C 语言编程中通常体现为内存复制(memcpy)操作。
“重叠-保留法” (Overlap-Save Method)的python实现
源码
import numpy as np
import matplotlib.pyplot as plt
import os
import shutil
from scipy.signal import firwin, lfilter
# ==========================================
# 1. 核心类:基于帧的 FIR 滤波器 (对应 C 代码逻辑)
# ==========================================
class FrameBasedFIR:
def __init__(self, coeffs, frame_size):
"""
初始化滤波器
coeffs: 滤波器系数 (B 数组)
frame_size: 每一帧处理的数据量 (BUFFER_COUNT)
"""
self.coeffs = coeffs
self.N = len(coeffs) - 1 # 滤波器阶数 (Order)
self.frame_size = frame_size
# 内部状态缓存
# 对应 C 代码中: static float Left[BUFFER_COUNT+N]
# 我们需要保留上一帧的最后 N 个数据作为下一帧的开头
self.history = np.zeros(self.N)
def process_frame(self, input_frame):
"""
处理单帧数据,对应 C 代码中的 ProcessBuffer 函数
"""
# 1. 构建扩展缓冲区 (Extended Buffer)
# 对应 C 代码逻辑:将历史数据 (Left[0...N]) 与当前帧数据组合
# 实际上 C 代码是利用指针偏移填入新数据,这里 Python 使用拼接模拟
extended_buffer = np.concatenate((self.history, input_frame))
# 2. 执行卷积 (FIR Filter)
# 对应 C 代码中的双重循环部分:
# for(j=0,k=i; j <= N; j++,k++) yLeft += Left[k] * B[j];
# 使用 'valid' 模式卷积,它只会计算完全重叠的部分,输出长度 = len(input_frame)
output_frame = np.convolve(extended_buffer, self.coeffs, mode='valid')
# 3. 更新历史数据 (关键步骤!)
# 对应 C 代码第 45-48 行:
# for(i=BUFFER_COUNT, j=0; i < BUFFER_COUNT+N; i++, j++) Left[j]=Left[i];
# 意思就是把当前帧最右边(末尾)的 N 个数据,保存下来给下一帧用
self.history = input_frame[-self.N:]
return output_frame
# ==========================================
# 2. 准备数据和环境
# ==========================================
# 创建输出目录
output_dir = "dsp_viz_results"
if os.path.exists(output_dir):
shutil.rmtree(output_dir)
os.makedirs(output_dir)
# 模拟参数
FS = 8000 # 采样率
DURATION = 0.1 # 秒
FRAME_SIZE = 64 # 每一帧的大小 (BUFFER_COUNT)
FILTER_ORDER = 32 # 滤波器阶数 (N)
# 生成信号:低频正弦波 (有用信号) + 高频噪声
t = np.linspace(0, DURATION, int(FS * DURATION), endpoint=False)
clean_signal = np.sin(2 * np.pi * 200 * t) # 200Hz 信号
noise = 0.5 * np.sin(2 * np.pi * 3000 * t) # 3000Hz 噪声
input_signal = clean_signal + noise
# 设计一个低通滤波器 (截止频率 1000Hz)
# 对应 C 代码中通过 Matlab 生成的 coeff.h
coeffs = firwin(numtaps=FILTER_ORDER + 1, cutoff=1000, fs=FS)
# ==========================================
# 3. 执行分帧处理
# ==========================================
processor = FrameBasedFIR(coeffs, FRAME_SIZE)
output_signal_list = []
# 将信号切片并逐帧送入滤波器
num_frames = len(input_signal) // FRAME_SIZE
for i in range(num_frames):
# 提取当前帧
start_idx = i * FRAME_SIZE
end_idx = start_idx + FRAME_SIZE
frame_data = input_signal[start_idx:end_idx]
# 调用我们的 C 逻辑复现函数
filtered_frame = processor.process_frame(frame_data)
output_signal_list.append(filtered_frame)
# 拼接所有帧的结果
output_signal_stitched = np.concatenate(output_signal_list)
# 为了对比,使用 Scipy 的标准一次性处理 (理想情况)
reference_output = lfilter(coeffs, 1.0, input_signal[:len(output_signal_stitched)])
# ==========================================
# 4. 可视化结果
# ==========================================
# 图 1: 整体波形对比
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.title("Original Input Signal (Frame Based Processing Input)")
plt.plot(input_signal[:len(output_signal_stitched)], color='lightgray', label='Noisy Input')
plt.plot(clean_signal[:len(output_signal_stitched)], 'g--', alpha=0.6, label='Ideal Clean Signal')
plt.legend()
plt.subplot(2, 1, 2)
plt.title("Filtered Output (Stitched Frames)")
plt.plot(output_signal_stitched, 'b', label='Frame-Based FIR Output')
plt.plot(reference_output, 'r:', label='Scipy lfilter (Reference)')
plt.legend()
plt.tight_layout()
plt.savefig(f"{output_dir}/1_full_waveform.png")
# 图 2: 放大帧边界 (验证边缘问题是否解决)
# 我们选取第 1 和 第 2 帧的交界处 (索引 64 附近)
boundary_idx = FRAME_SIZE
zoom_range = 20
plt.figure(figsize=(10, 5))
plt.title(f"Zoom at Frame Boundary (Index {boundary_idx})")
plt.plot(range(boundary_idx - zoom_range, boundary_idx + zoom_range),
output_signal_stitched[boundary_idx - zoom_range : boundary_idx + zoom_range],
'b-o', markersize=4, label='Stitched Output')
# 画一条竖线表示帧的分割线
plt.axvline(x=boundary_idx - 0.5, color='k', linestyle='--', alpha=0.5, label='Frame Boundary')
plt.text(boundary_idx - 5, max(output_signal_stitched)*0.8, "Frame 1 End", ha='right')
plt.text(boundary_idx + 5, max(output_signal_stitched)*0.8, "Frame 2 Start", ha='left')
plt.legend()
plt.grid(True, alpha=0.3)
plt.savefig(f"{output_dir}/2_boundary_zoom.png")
# 图 3: 缓冲区工作原理图解
plt.figure(figsize=(10, 4))
plt.axis('off')
plt.title("Buffer Logic Visualization (Overlap-Save)", fontsize=14)
# 绘制示意框
def draw_box(x, y, width, height, text, color, label=None):
rect = plt.Rectangle((x, y), width, height, facecolor=color, edgecolor='black', alpha=0.7)
plt.gca().add_patch(rect)
plt.text(x + width/2, y + height/2, text, ha='center', va='center', fontweight='bold')
if label:
plt.text(x + width/2, y - 0.2, label, ha='center', va='top', fontsize=9)
# 历史区
draw_box(0, 0, 3, 1, "History\n(Previous Tail)", "#FFD700", f"Left[0]...Left[{FILTER_ORDER-1}]")
# 当前帧
draw_box(3, 0, 7, 1, "Current Frame\n(Input Data)", "#87CEEB", f"Left[{FILTER_ORDER}]...Left[{FRAME_SIZE+FILTER_ORDER}]")
# 移动操作箭头
plt.arrow(8, 1.1, -6.5, 0.5, head_width=0.2, head_length=0.2, fc='k', ec='k')
plt.text(4.5, 1.8, "Copy Tail to Head for Next Step", ha='center')
plt.xlim(-1, 11)
plt.ylim(-1, 3)
plt.savefig(f"{output_dir}/3_buffer_logic.png")
print(f"可视化完成!图片已保存至文件夹: {output_dir}")
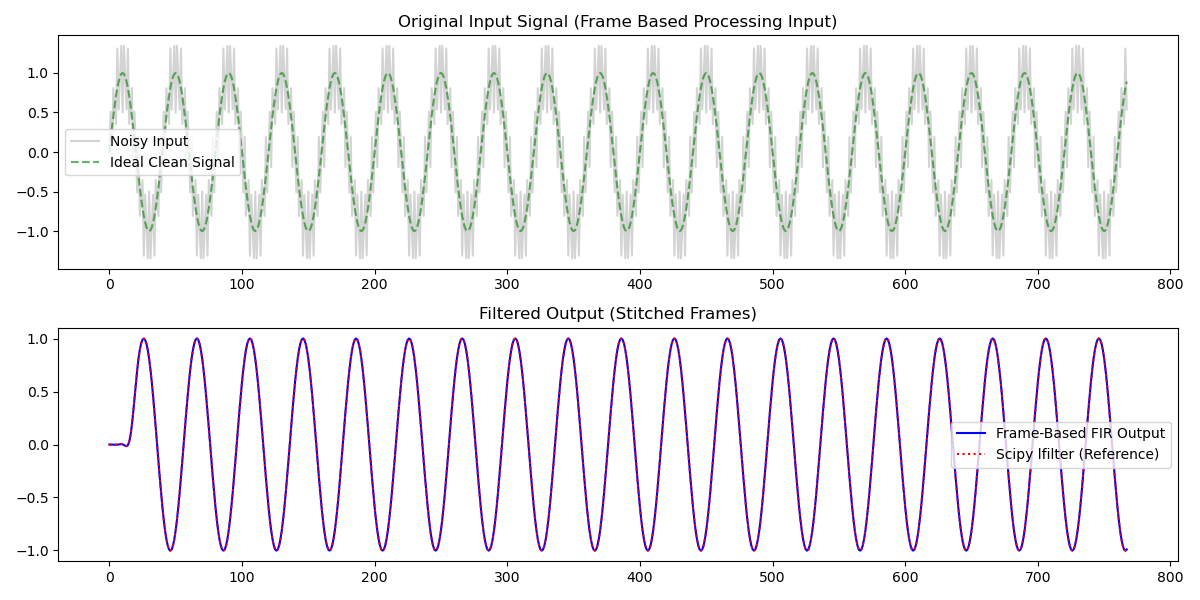
print("1. 1_full_waveform.png: 展示滤波前后的完整波形。")
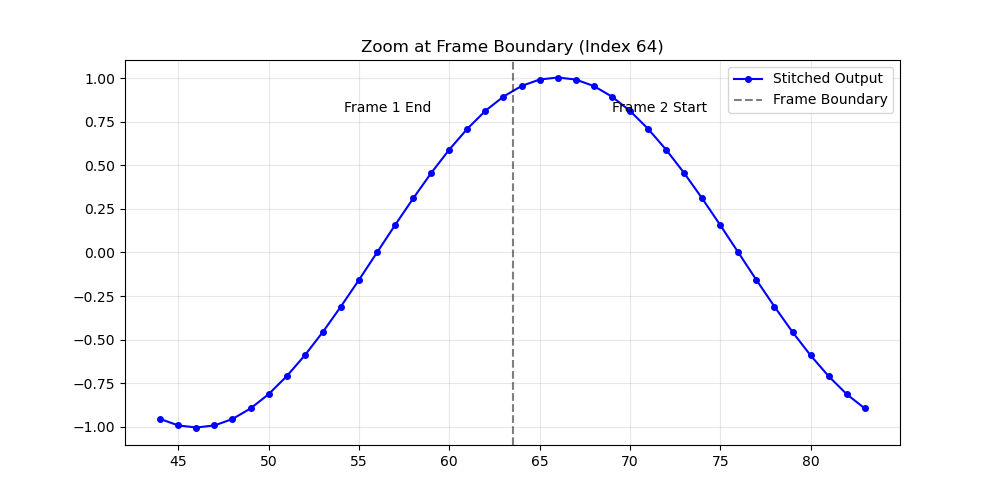
print("2. 2_boundary_zoom.png: 展示帧与帧交界处的平滑连接(证明消除了边缘效应)。")
print("3. 3_buffer_logic.png: 缓冲区结构示意图。")
结果






















 1966
1966

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








