代码随想录算法训练营第 48 天 | 42. 接雨水、84. 柱状图中最大的矩形

42. 接雨水

题目链接

方法一：单调栈

思路：
如果待加入元素大于栈顶元素，则：

• 待加入元素为栈顶元素右边更高的柱子。
• 栈顶下面的元素为栈顶元素左边更高的柱子。

遇到连续相等的柱子，即可把重复值弹出再压栈，也可直接压栈。
（直接压栈后面计算时高度为 0，对结果不影响。）

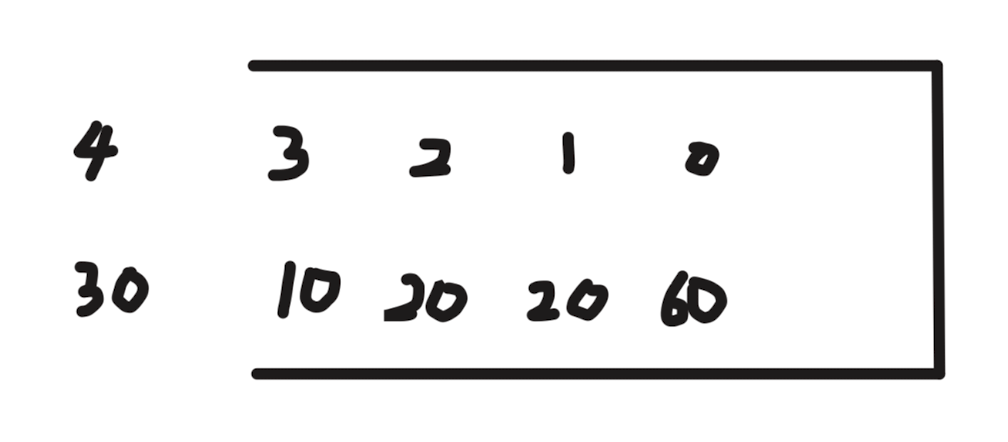
h = Math.min(height[i], height[stack.peek()]) - height[index]
高度为右边更高的柱子和左边更高的柱子的最小值，还要减去当前柱子的高度！

w = i - stack.peek() - 1

重点：
单调栈是横向遍历！

时间复杂度：O(n)
空间复杂度：O(n)

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int result = 0;
        Stack<Integer> stack = new Stack<>();
        
        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int index = stack.pop();
                if (!stack.isEmpty()) { // 需要判断一下栈不为空，即栈下面还有元素。
                    int h = Math.min(height[i], height[stack.peek()]) - height[index]; // 高度为右边更高的柱子和左边更高的柱子的最小值，还要减去当前柱子的高度！
                    int w = i - stack.peek() - 1;
                    result += h * w;
                }
            }
            stack.push(i);
        }
        
        return result;
    }
}

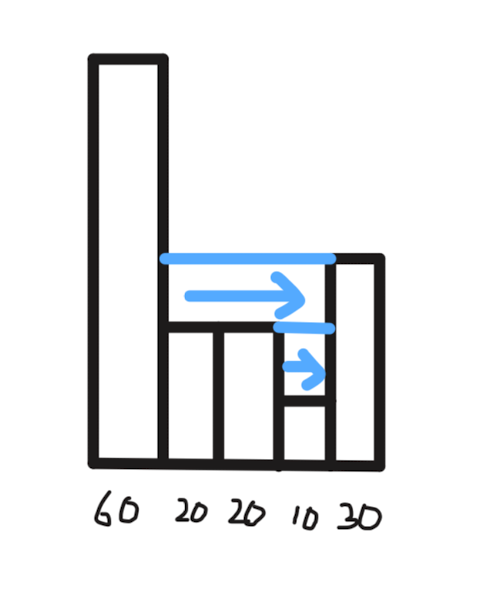
方法二：双指针 / 动态规划

创建两个数组，分别表示当前柱子左边最高柱子（包括自身）的高度和右边最高柱子（包括自身）的高度。

如何求左边最高柱子的高度：
左边最高柱子高度 = 它左边柱子的左边最高柱子的高度和它本身高度，取最大值。

根据木桶效应，某个位置能装的水的高度为左边最高柱子高度和右边最高柱子高度的最小值。

易错点：

• 求出短板后，不要忘了减自身高度。

时间复杂度：O(n)
空间复杂度：O(n)

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int result = 0;
        int[] leftMax = new int[n]; // 左边最高柱子的高度
        int[] rightMax = new int[n]; // 右边最高柱子的高度
        leftMax[0] = height[0];
        rightMax[n - 1] = height[n - 1];

        for (int i = 1; i < rightMax.length; i++) { // i 从 1 开始即可
            leftMax[i] = Math.max(leftMax[i - 1], height[i]);
        }
        for (int i = n - 2; i >= 0; i--) { // i 从 n - 2 开始即可
            rightMax[i] = Math.max(rightMax[i + 1], height[i]);
        }

        for (int i = 0; i < n; i++) {
            result += Math.min(leftMax[i], rightMax[i]) - height[i];
        }

        return result;
    }
}

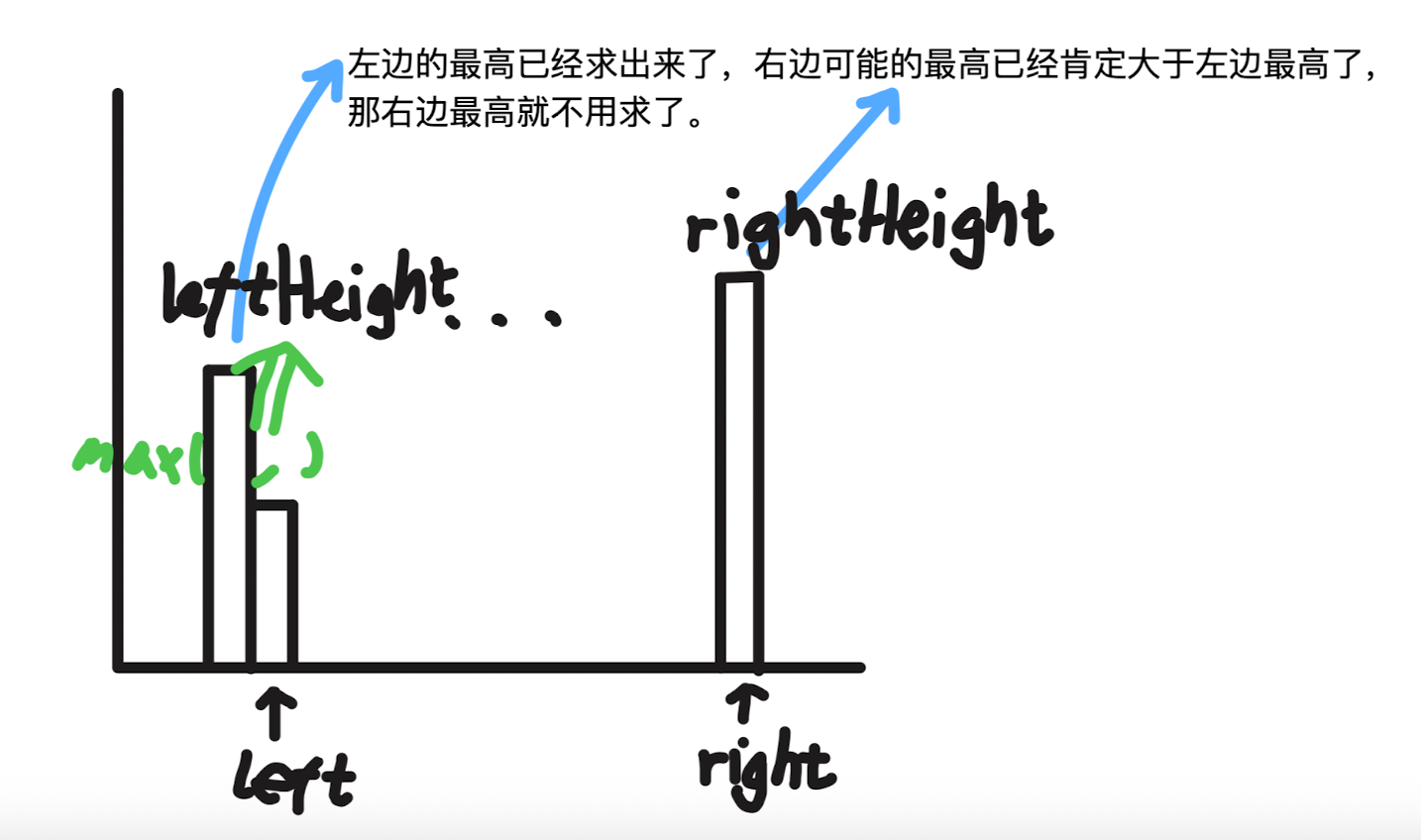
方法三：双指针优化

思路同方法二，但是不创建两个数组，改为创建两个双指针 left 和 right。

基于这样的原理：
某个位置，已经知道它左边最高柱子的高度，它右边最高柱子的高度还没求。
但是知道它右边某个柱子的右边最高柱子高度是大于上面已经求出来的左边最高柱子的高度。
那么这个位置右边最高柱子的高度就不用求了。因为再怎么求，也会大于等于它右边某个柱子求出来的右边最高柱子的高度。

易错点：

• while 循环中 left 和 right 可以相等
• 求出短板后，不要忘了减自身高度。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int result = 0;
        int leftHeight = height[0]; // 左边柱子（包括自身）的最大高度
        int rightHeight = height[n - 1]; // 右边柱子（包括自身）的最大高度
        int left = 1;
        int right = n - 2;

        // 也可以写成：
        // int leftHeight = 0;
        // int rightHeight = 0;
        // int left = 0;
        // int right = n - 1;

        while (left <= right) { // 必须要包括 "="
            leftHeight = Math.max(leftHeight, height[left]); // 不知道上个循环是哪个更新，索性两个都更新
            rightHeight = Math.max(rightHeight, height[right]);

            if (leftHeight < rightHeight) {
                result += leftHeight - height[left];
                left++;
            } else {
                result += rightHeight - height[right];
                right--;
            }
        }

        return result;
    }
}

附录：
单调栈方法和双指针方法的本质不同：

• 单调栈
  • 单调栈是找左边和右边更高的柱子。
  • 是横向遍历。
• 双指针
  • 双指针是找左边和右边最高的柱子 。
  • 是纵向遍历。

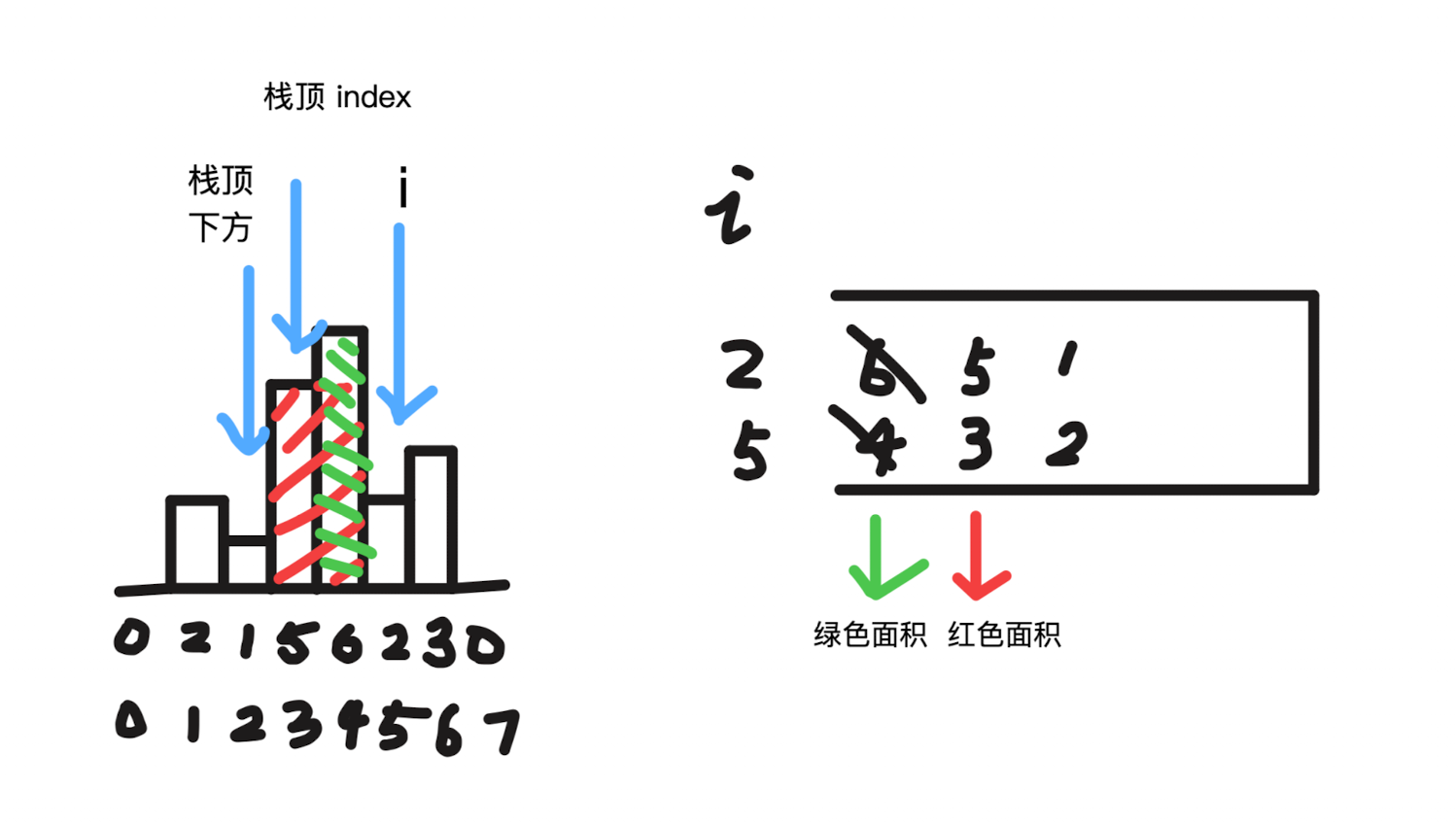
84. 柱状图中最大的矩形

题目链接

与接雨水的区别：

• 本题是找右边和左边第一个更小的柱子；接雨水是找更大。
• 本题最左边和最右边柱子也要用上；接雨水最左边和最右边柱子肯定接不了雨水。

小技巧：
数组前后都填 0，充当哨兵。

h = heights[index]。
高度为当前元素高度
w = i - stack.peek() - 1
宽度为找到右边和左边第一个更小的柱子之差。

求出最大的面积。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int result = 0;
        Stack<Integer> stack = new Stack<>();

        int[] heights2 = new int[n + 2];
        System.arraycopy(heights, 0, heights2, 1, n); // 首尾填 0
        heights = heights2;

        for (int i = 0; i < n + 2; i++) { // 遍历 n + 1 次
            while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
                int index = stack.pop();
                if (!stack.isEmpty()) {
                    int h = heights[index]; // 高度为当前元素高度
                    int w = i - stack.peek() - 1; // 宽度为找到右边和左边第一个更小的柱子之差
                    result = Math.max(result, h * w);
                }
            }
            stack.push(i);
        }

        return result;
    }
}

双指针法，略：

难就难在本题要记录记录每个柱子 左边第一个小于该柱子的下标，而不是左边第一个小于该柱子的高度。
所以需要循环查找，也就是在寻找的过程中使用了 while