Floyd 算法精讲
注意是无向图。
Floyd 算法适用于稠密图,时间复杂度是 O(V^3)
对边的权值正负没有要求,都可以处理。
核心思想是动态规划。
动规五部曲:
-
确定 dp 数组含义:
- 三维 dp 数组:dp[i][j][k]。从起点 i 到 终点 j 以 [1…k] 集合中的一个节点为中间节点的最短距离。
- 二维 dp 数组:dp[i][j]。从起点 i 到终点 j 的最短距离。
-
递推公式:
- 三维:dp[i][j][k] = Math.min(dp[i][k][k - 1] + dp[k][j][k - 1], dp[i][j][k - 1])
经过节点 k:dp[i][j][k] = dp[i][k][k - 1] + dp[k][j][k - 1]
不经过节点 k:dp[i][j][k] = d[i][j][k - 1]- 二维:dp[i][j] = Math.min(dp[i][k] + dp[k][j], dp[i][j]);
经过中间节点 k:dp[i][j] = dp[i][k] + dp[k][j]
不经过中间节点:dp[i][j] = d[i][j] -
dp 数组如何初始化:本题求的是最小值,所以输入数据没有涉及到的节点的情况都应该初始为一个最大数,本题为 10005。
- 三维:dp[s][t][0] = val, dp[t][s][0] = val
- 二维:dp[s][t] = val, dp[t][s][0] = val
-
确定遍历顺序:k 必须放在最外层遍历。
-
打印 dp 数组。
三维数组法:(不推荐。第 3 维理解起来有点晕。)
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[][][] dp = new int[n + 1][n + 1][n + 1];
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < n + 1; j++) {
Arrays.fill(dp[i][j], 10005); // 三维数组全部初始化为比最大 val 稍大点的 10005
}
}
while (m-- > 0) {
int s = sc.nextInt();
int t = sc.nextInt();
int val = sc.nextInt();
dp[s][t][0] = val;
dp[t][s][0] = val; // 无向图
}
for (int k = 1; k < n + 1; k++) { // k 必须在最外层
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
dp[i][j][k] = Math.min(dp[i][k][k - 1] + dp[k][j][k - 1], dp[i][j][k - 1]);
}
}
}
int q = sc.nextInt();
while (q-- > 0) {
int start = sc.nextInt();
int end = sc.nextInt();
if (dp[start][end][n] != 10005) { // 不等于默认值输出值
System.out.println(dp[start][end][n]);
} else { // 等于默认值输出 -1,表示无法到达
System.out.println(-1);
}
}
}
}
二维数组法:(推荐)
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[][] dp = new int[n + 1][n + 1];
for (int i = 0; i < n + 1; i++) {
Arrays.fill(dp[i], 10005); // 二维数组全部初始化为比最大 val 稍大点的 10005
}
while (m-- > 0) {
int s = sc.nextInt();
int t = sc.nextInt();
int val = sc.nextInt();
dp[s][t] = val;
dp[t][s] = val; // 无向图
}
for (int k = 1; k < n + 1; k++) { // k 必须在最外层
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
dp[i][j] = Math.min(dp[i][k] + dp[k][j], dp[i][j]);
}
}
}
int q = sc.nextInt();
while (q-- > 0) {
int start = sc.nextInt();
int end = sc.nextInt();
if (dp[start][end] != 10005) { // 不等于默认值输出值
System.out.println(dp[start][end]);
} else { // 等于默认值输出 -1,表示无法到达
System.out.println(-1);
}
}
}
}
A* 算法精讲(A star 算法)
就是改良版的广搜,只不过从队列取出元素时,按 F = G + H 排序,优先取出离终点近的。
广搜复杂度:O(n^2)
A* 复杂度:O(d * logd),d 为起点到终点的深度。
计算欧式距离时,统一不开根号,这样可以保证精度。
G:起点到当前节点的距离(真实距离)
H:当前节点到终点的距离(估计距离)
F:G + H
有真实距离用真实距离,没有真实距离用评估的距离
初始化:int[][] move = new int[1001][1001],既起到记录步数作用,又起到判断节点有没有访问过作用。
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
// 8 个方向
public static int[][] dir = {{1, 2}, {-1, 2}, {1, -2}, {-1, -2}, {2, 1}, {-2, 1}, {2, -1}, {-2, -1}};
// 内部类,表示当前点信息
public static class Knight {
int x, y; // 当前节点坐标
int g; // 起点到当前节点真实距离
int h; // 当前节点到终点预估距离
int f; // g + h
public Knight(int x, int y, int g, int h, int f) {
this.x = x;
this.y = y;
this.g = g;
this.h = h;
this.f = f;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n-- > 0) {
int x1 = sc.nextInt();
int y1 = sc.nextInt();
int x2 = sc.nextInt();
int y2 = sc.nextInt();
Astar(x1, y1, x2, y2); // 调用 A* 算法
}
}
public static void Astar(int x1, int y1, int x2, int y2) {
Knight start = new Knight(x1, y1, 0, calDist(x1, y1, x2, y2), calDist(x1, y1, x2, y2)); // 初始化 起点节点
PriorityQueue<Knight> pq = new PriorityQueue<>((a, b) -> a.f - b.f); // 优先级队列,以 f 升序排序
pq.offer(start);
int[][] move = new int[1001][1001]; // 记录有没有访问过和步数,0 代表未访问(起点除外)
while (!pq.isEmpty()) {
Knight cur = pq.poll();
if (cur.x == x2 && cur.y == y2) { // 如果已经到达终点
break;
}
for (int i = 0; i < 8; i++) {
int nextX = dir[i][0] + cur.x;
int nextY = dir[i][1] + cur.y;
if (nextX < 1 || nextX > 1000 || nextY < 1 || nextY > 1000) {
continue;
}
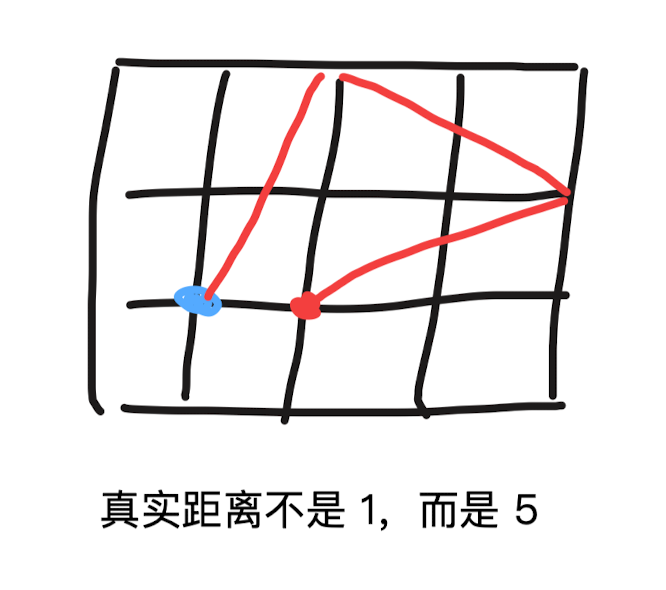
int g = cur.g + 5; // 真实距离加 1^2 + 2^2 = 5
int h = calDist(nextX, nextY, x2, y2); // 预估距离
int f = g + h;
Knight next = new Knight(nextX, nextY, g, h, f);
// 因为是广度优先,所以第一次访问节点时的步数就是最小的,不会出现被覆盖情况
if (move[nextX][nextY] == 0 && !(nextX == x1 && nextY == y1)) { // 当节点未访问时(因为用 0 来判断节点未访问,所以需要对起点特判)
move[nextX][nextY] = move[cur.x][cur.y] + 1; // 步数加 1
pq.offer(next);
}
}
}
System.out.println(move[x2][y2]); // 输出到终点(x2, y2)的步数
}
// 计算两个点的欧氏距离
public static int calDist(int x1, int y1, int x2, int y2) {
return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
}
图算法总结
无向图:
- DFS
- BFS
最小生成树(MST):
- Prim:稠密图,时间复杂度为 O(V^2)。
- Kruskal:稀疏图,时间复杂度为 O(E * logE)。
最短路径:
- BFS:无向图且权值都为 1,相当于无权图。
- Dijstra:有向图、单源、权值正数。
- 朴素法:稠密图,时间复杂度为 O(V^2)。
- 堆优化法:稀疏图,时间复杂度为 O(E * logE)。
- Bellman_ford:有向图、单源点、权值可以为负数 或者 检测负权环路 或者 有限节点最短路径。
- 普通:稠密图,时间复杂度为 O(V * E)。
- 队列优化:稀疏图,O(V * K)。K 为每个节点的平均出度。
- Floyd:有向图、多源点、权值可以为负数。适合稠密图。时间复杂度为 O(V^3)。
BFS 和 Dijkstra 区别:在搜索最短路的时候, 如果是无权图(边的权值都是 1) 那就用广搜,代码简洁,时间效率和 Dijkstra 差不多 (具体要取决于图的稠密)





















 1234
1234

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








