代码随想录算法训练营第 15 天 | 513. 找树左下角的值、112. 路径总和、113. 路径总和 II、106. 从中序与后序遍历序列构造二叉树、105. 从前序与中序遍历序列构造二叉树

513. 找树左下角的值

题目链接

思路：
递归法，把深度作为递归函数的参数传进去。如果深度变大，则更新 result 的值。因为是先左后右，所以最深层碰到的第一个节点即满足要求。

前中后序遍历都可，因为只要先遍历左再遍历右就行

易错点：

1. 对题目的理解：树左下角的值也可能是右孩子
2. 因为定义的是类的全局变量。所以最好在方法中再初始化一次 int maxDepth = Integer.MIN_VALUE，防止多次调用该方法

使用全局变量一定记得每次主函数对它进行初始化，它会重复进行测试

class Solution {
    int maxDepth = Integer.MIN_VALUE;
    int result = 0;

    public int findBottomLeftValue(TreeNode root) {
        int maxDepth = Integer.MIN_VALUE; // 最好在这加一句，防止多次调用该方法
        traversal(root, 0);
        return result;
    }

    public void traversal(TreeNode root, int depth) {
        if (root.left == null && root.right ==null) {
            if (depth > maxDepth) {
                maxDepth = depth;
                result = root.val;
            }
            return;
        }

        if (root.left != null) { // 左
            depth++;
            traversal(root.left, depth); // 可把这三行简化成 traversal(root.left, depth + 1)
            depth--;
        }
        if (root.right != null) { // 右
            depth++;
            traversal(root.right, depth); // 可把这三行简化成 traversal(root.left, depth + 1)
            depth--;
        }
    }
}

总结：

depth++;
traversal(root.left, depth);
depth--;

等价于

traversal(root.left, depth + 1)

---

其他方法：层序遍历

一个巧妙的思路：
先加入右孩子，再加入左孩子。这样最后一个节点即为题目要求值。

代码略

---

112. 路径总和

题目链接

Trick：
将 target 传进去减减判断等不等于 0，而不是将 0 传进去判断等不等于 target

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        return traversal(root, targetSum - root.val);
    }

    public boolean traversal(TreeNode root, int count) {
        if (root.left == null && root.right == null && count == 0) {
            return true;
        }
        if (root.left != null) {
            count -= root.left.val;
            if (traversal(root.left, count)) {
                return true;
            }
            count += root.left.val;
        }
        if (root.right != null) {
            count -= root.right.val;
            if (traversal(root.right, count)) {
                return true;
            }
            count += root.right.val;
        }
        return false;
    }
}

---

官解更简洁：

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}

---

总结：

递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的 113.路径总和 ii）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在 236. 二叉树的最近公共祖先 中介绍）
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

---

113. 路径总和 II

题目链接

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        if (root == null) {
            return result;
        }
        traversal(root, targetSum - root.val, path, result);
        return result;
    }

    public void traversal(TreeNode root, int count, List<Integer> path, List<List<Integer>> result) {
        path.add(root.val);
        if (root.left == null && root.right == null && count == 0) {
            result.add(new ArrayList<>(path));
        }

        if (root.left != null) {
            traversal(root.left, count - root.left.val, path, result);
            path.remove(path.size() - 1);
        }

        if (root.right != null) {
            traversal(root.right, count - root.right.val, path, result);
            path.remove(path.size() - 1);
        }
    }
}

---

!! 注：

    public void traversal(TreeNode root, int count, List<Integer> path, List<List<Integer>> result) {
        path.add(root.val);
        if (root.left == null && root.right == null && count == 0) {
            result.add(new ArrayList<>(path));
        }

        if (root.left != null) {
            traversal(root.left, count - root.left.val, path, result);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            traversal(root.right, count - root.right.val, path, result);
            path.remove(path.size() - 1);
        }
    }

也可以写成：

    public void traversal(TreeNode root, int count, List<Integer> path, List<List<Integer>> result) {
        path.add(root.val);
        if (root.left == null && root.right == null && count == 0) {
            result.add(new ArrayList<>(path));
        }

        if (root.left != null) {
            traversal(root.left, count - root.left.val, path, result);
        }
        if (root.right != null) {
            traversal(root.right, count - root.right.val, path, result);
        }
        path.remove(path.size() - 1);
    }

我的理解是：
前者是从 个体 的角度考虑的，我认为我的递归函数每次遍历完会添加一个节点，所以我遍历完要把它 remove 掉。

后者是从 全局 的角度考虑的，写成后者这种形式，总共只有一个 add 和 remove，所以一轮遍历完后不会改变 path，那么两个 traversal 之间也不用加 remove 了。

体现出一种 相信的力量

见讨论

---

106. 从中序与后序遍历序列构造二叉树

题目链接

inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]

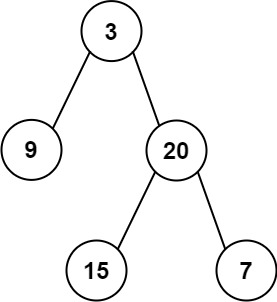
步骤：

1. 后序数组为空，返回 null
2. 后序数组最后一个元素为根节点元素
3. 寻找中序数组位置作为切割点
4. 切中序数组
5. 切后序数组
6. 递归处理切下来的中序数组和后序数组

重点：

1. 切数组

切中序用 index
切后序用 中序数组里的左数组长度

中序数组截掉作为根的数
后序数组截掉最后一个数

2. 递归处理
   root.left = traversal(左中序, 左后序);
root.right = traversal(右中序, 右后序);

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (postorder.length == 0) {
            return null;
        }

        // 只有 1 个元素，直接返回
        TreeNode root = new TreeNode(postorder[postorder.length - 1]);
        if (postorder.length == 1) {
            return root;
        }

        // 找中序数组根节点位置
        int index = 0;
        for (; index < postorder.length; index++) {
            if (inorder[index] == root.val) {
                break;
            }
        }

        // 切中序
        int[] leftInOrder = subArray(inorder, 0, index); // 左中序
        int[] rightInOrder = subArray(inorder, index + 1, inorder.length); // 右中序

        // 切后序
        int[] leftPostOrder = subArray(postorder, 0, leftInOrder.length); // 左后序，切与“左中序”相等的长度
        int[] rightPostOrder = subArray(postorder, leftInOrder.length, postorder.length - 1); // 右后序

        // 递归处理
        root.left = buildTree(leftInOrder, leftPostOrder);
        root.right = buildTree(rightInOrder, rightPostOrder);
        
        return root;
    }

    // 返回子数组，左闭右开
    public int[] subArray(int[] arr, int start, int end) {
        if (start < 0 || end > arr.length || start >= end) {
            return new int[0]; // 下标不满足条件，返回空数组
        }
        int newLen = end - start;
        int[] newArr = new int[newLen];
        for (int i = 0; i < newLen; i++) {
            newArr[i] = arr[i + start];
        }
        return newArr;
    }
}

待优化，见下一题：

1. 用 Arrays.copyOfRange 代替自己写的
2. 把时间复杂度从 O(n * n) 优化到 O(n)

• 用 哈希表 保存中序数组位置索引，避免频繁遍历查询根节点位置
• 用指针代替数组，避免频繁创建数组开销

---

105. 从前序与中序遍历序列构造二叉树

题目链接

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

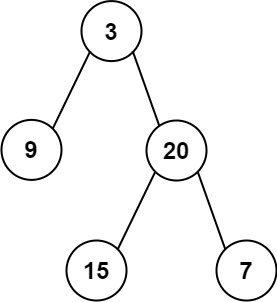
完全优化的版本：

class Solution {
    HashMap<Integer, Integer> map = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        
        return traversal(inorder, preorder, 0, preorder.length, 0, inorder.length);
    }

    // 递归函数，左闭右开
    public TreeNode traversal(int[] inorder, int[] preorder, int leftInOrder, int rightInOrder, int leftPreOrder, int rightPreOrder) {
        // leftPreOrder = rightPreOrder 时，已经是空数组
        if (leftPreOrder >= rightPreOrder) {
            return null;
        }

        // 把根节点构建出来
        TreeNode root = new TreeNode(preorder[leftPreOrder]);

        // 找中序数组根节点位置
        int index = map.get(preorder[leftPreOrder]);

        // 得到左子树中的节点数目
        int sizeLeftSubTree = index - leftInOrder;

        // 中序数组四个指针
        int llInOrder = leftInOrder;
        int lrInOrder = index;

        int rlInOrder = index + 1;
        int rrInOrder = rightInOrder;

        // 前序数组四个指针
        int llPreOrder = leftPreOrder + 1; // 截掉第一个
        int lrPreOrder = leftPreOrder + 1 + sizeLeftSubTree; // 因为肯定和中序数组左子树长度一样
        int rlPreOrder = leftPreOrder + 1 + sizeLeftSubTree;
        int rrPreOrder = rightPreOrder;

        // 递归，左闭右开。左中对左前，右中对右前。
        root.left = traversal(inorder, preorder, llInOrder, lrInOrder, llPreOrder, lrPreOrder);
        root.right = traversal(inorder, preorder, rlInOrder, rrInOrder, rlPreOrder, rrPreOrder);

        return root;        
    }
}

---

补充：
前序和后序不能唯一确定一颗二叉树，如：

        1
      /
    2
  /
3

前序 1、2、3
中序 3、2、1
后序 3、2、1

和

        1
          \
            2
              \
                3

前序 1、2、3
中序 1、2、3
后序 3、2、1

前序遍历都是 1、2、3
后序遍历后生 3、2、1

---

最后的最后：
1024 程序员节快乐！