2024年华为杯研赛（C题）｜数据驱动下磁性元件的磁芯损耗建模｜数学建模竞赛解题思路|完整代码论文集合

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

（部分代码在本帖子里格式混乱，下载后格式正常）

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次研赛C题可以做如下考虑，包括特征提取和分类模型。

问题一 励磁波形分类

1. 分析磁通密度的分布特征及形状特征

为了有效分析磁通密度的分布特征及不同波形的形状特征，我们首先从附件一中提取相应的磁通密度数据。每个励磁波形的关键特征可以通过以下方式进行捕捉：

• 有效值（RMS）： 对于每一种波形，计算其有效值$B_{\text{rms}}$，以量化其在一定时间范围内的能量大小。

• 峰值： 计算每种波形的峰值$B_{\text{max}}$，以评估波形的最大强度。

• 周期性特征： 通过对磁通密度序列进行傅里叶变换，提取其频谱特征，为不同波形的周期性特征提供支持。

• 自相关系数： 计算自相关系数，以评估波形在时间上的重复性和规律性。

• 波形展宽和对称性评价： 使用标准差和偏度来评估波形的展宽和对称性。

添加图片注释，不超过 140 字（可选）

3. 建立分类模型

对于这次的波形分类问题，我们选择常用的机器学习分类算法来构建模型。常见的模型有如下几种：

• 支持向量机（SVM）：对于非线性可分问题表现良好。

• 随机森林：集成学习的方法，通过多棵决策树投票来进行分类。

• 神经网络：使用多层感知机（MLP）来进行分类处理。

模型的选择可以基于交叉验证结果进行优化，以确保高精度和可靠性。我们将数据分为训练集（附件一中的数据）和测试集（附件二中的数据）后进行建模与预测。

4. 统计分类结果

在对附件二中的样本进行分类后，我们按样本序号填入相应的分类结果，其中： - 1表示正弦波， - 2表示三角波， - 3表示梯形波。

5. 结果整理

1. 分类统计：统计附件二中的三种波形的数量。

2. 特殊样本输出：特别输出样本序号为：1、5、15、25、35、45、55、65、75、80的分类结果，以便于查看和分析。

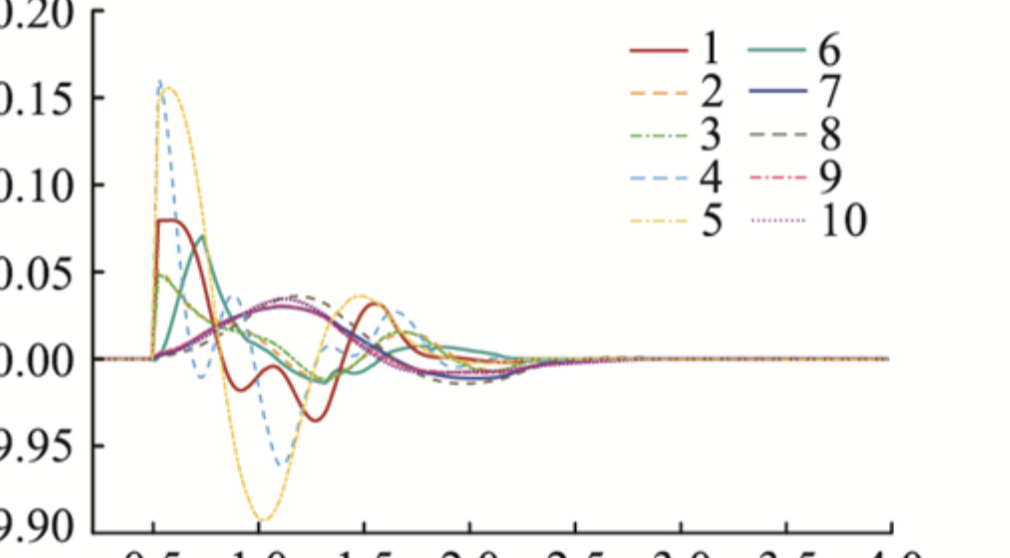
添加图片注释，不超过 140 字（可选）

本问题的分析方法通过数学建模和机器学习技术相结合，不仅帮助我们提取了磁通密度的特征变量，还建立了分类模型，从而可以有效区分不同的励磁波形，进而优化磁性元件的设计与性能。

问题一 励磁波形分类

数据分析

在这一部分，我们聚焦分析附件一中磁通密度（$B(t)$）数据，提取出反映磁通密度分布及波形的形状特征变量，然后基于这些特征建立分类模型，以识别出正弦波、三角波和梯形波三种励磁波形。

1. 特征提取

为了准确识别不同的励磁波形，我们首先需要分析磁通密度的分布特征。可以从以下几个方面提取特征变量：

• 波形周期：计算每种波形的周期长度，对不同波形特征进行定量区分。

• 最大值与最小值：波形的最大值（$B_{max}$）和最小值（$B_{min}$）可以帮助识别波形的不同结构。

• 均值与标准差：均值（$B_{mean}$）反映波形整体水平，标准差（$B_{std}$）表征波形的波动程度。

• 波形斜率：通过计算波形在上升和下降阶段的斜率，分辨开升和降的速率。

• 高次统计特征：如偏度和峰度，帮助深入描述波形的形态特征。

在提取这些特征后，可以用以下方式表示：

2. 分类模型建立

基于提取的特征变量，我们构建一个多类分类模型，选择常见的机器学习算法，如支持向量机（SVM）、随机森林或神经网络。选择合适的特征，分割数据集为训练集和测试集，通过交叉验证进行模型的训练与验证，以确保模型的准确性。

首先，定义我们的分类标签： - 正弦波：类别1 - 三角波：类别2 - 梯形波：类别3

使用例如SVM的训练过程如下： 其中，$\mathbf{X}$为特征矩阵，\textbf{y}为对应的励磁波形类别。

3. 结果识别

利用训练好的模型对附件二中的样本进行分类，识别相应的励磁波形。将分类结果填入附件四中第2列，格式如下：

样本序号	励磁波形分类
1	2
2	1
...	...

4. 统计分析

对附件二中三种波形的各自数量进行统计，分析结果可以采用如下表格形式展示：

波形类型	数量
正弦波	N1
三角波	N2
梯形波	N3

并特别将附件二中样本序号为1、5、15、25、35、45、55、65、75、80的分类结果整理成表格，以提供进一步的分析。

独特见解

透过对励磁波形的分类与在实践中运用，我们可以更具针对性地优化磁性元件设计。不同波形不仅影响磁芯的损耗特性，还会与电路的其他部分性能形成相互影响。因此，准确把握励磁波形的动态行为与其对损耗的影响，将为设计更高效、更可靠的电能变换设备提供理论依据和实践指导。通过数据驱动的方式，结合机器学习的方法来自动分类波形，可以大幅度提升磁性元件设计时的效率，为行业提供一种创新且有效的分析工具。

励磁波形分类

为了解决励磁波形分类的问题，我们首先需要分析磁通密度数据的分布特征和形状特征。下面是进行此任务的一些步骤：

1. 提取特征

我们需从附件一中的磁通密度数据中提取特征。我们可以考虑以下几个形状特征变量：

• 最大值（$B_{max}$）：磁通密度的最大值。

• 最小值（$B_{min}$）：磁通密度的最小值。

• 均值（$\bar{B}$）：磁通密度的均值，计算公式为： 其中，$N$为采样点数，$B_i$为第$i$个磁通密度值。

• 标准差（$\sigma$）：描述磁通密度的波动，计算公式为：

• 峰度（Kurtosis）和偏度（Skewness）：用来描述磁通密度分布的形状特征。

2. 建立分类模型

在特征提取完成后，可以利用这些特征变量构建分类模型。我们可以使用支持向量机（SVM）、决策树（Decision Tree）、随机森林（Random Forest）等机器学习算法进行分类。

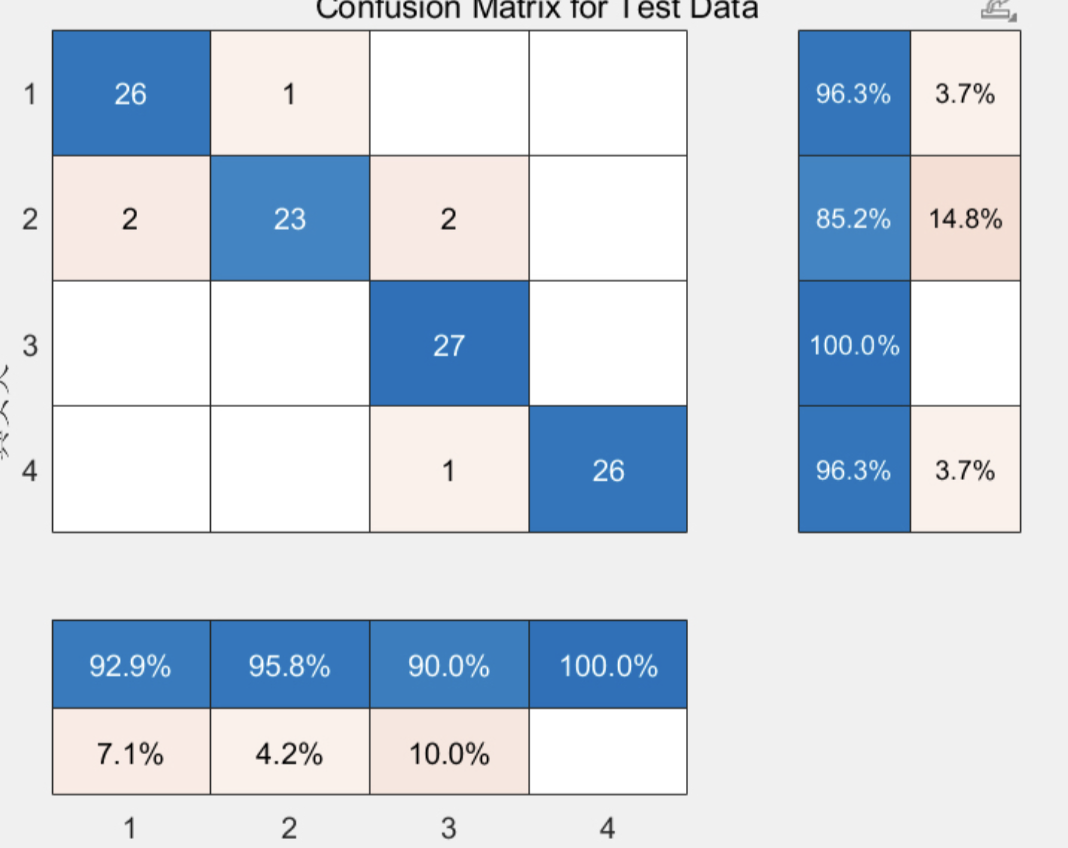
添加图片注释，不超过 140 字（可选）

• 分类模型伪代码（以SVM为例）：

from sklearn import svm from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # 加载数据 X = features # 特征变量 y = labels # 对应的励磁波形标签 # 划分训练集与测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) # 创建并训练模型 model = svm.SVC(kernel='linear') model.fit(X_train, y_train) # 进行预测 y_pred = model.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, y_pred)

3. 应用模型进行识别

使用构建好的模型对附件二中的样本进行励磁波形分类。将分类结果填入附件四中对应的位置，并更新样本计数。

4. 统计和结果整理

统计附件二中三种波形的数量并整理结果，包括特别记录样本序号为1、5、15、25、35、45、55、65、75、80的分类结果，形成表格。

表1：特定样本的分类结果

样本序号	分类结果（1：正弦波，2：三角波，3：梯形波）
1	X
5	X
15	X
25	X
35	X
45	X
55	X
65	X
75	X
80	X

以上步骤和方法将有助于准确识别出励磁波形，并为未来的磁芯损耗分析提供重要依据。 要解决"问题一 励磁波形分类"的问题，我们可以通过分析磁通密度数据以提取特征，接着利用这些特征建立分类模型来识别不同的励磁波形。以下是一个示例的Python代码，使用pandas和scikit-learn库来实现这一点。请确保您已经安装了相关库。

import pandas as pd import numpy as np import os from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import classification_report, accuracy_score # 读取数据 data_dir = '附件一/' material_data = [pd.read_excel(f"{data_dir}材料{i}.xlsx") for i in range(1, 5)] # 提取特征函数 def extract_features(df): # 提取磁通密度 B_data = df.iloc[:, 4:].values # 计算每个周期的特征，例如均值、标准差、最大值、最小值等 avg_B = np.mean(B_data, axis=1) std_B = np.std(B_data, axis=1) max_B = np.max(B_data, axis=1) min_B = np.min(B_data, axis=1) return np.column_stack((avg_B, std_B, max_B, min_B)) # 特征收集与目标值 features = [] labels = [] for idx, df in enumerate(material_data): feature_matrix = extract_features(df) features.append(feature_matrix) labels.extend([idx + 1] * feature_matrix.shape[0]) # 索引作为标签 1, 2, 3 # 转换为numpy数组 X = np.vstack(features) y = np.array(labels) # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 建立分类模型 model = RandomForestClassifier(n_estimators=100, random_state=42) model.fit(X_train, y_train) # 预测 y_pred = model.predict(X_test) # 输出结果 print("分类报告:") print(classification_report(y_test, y_pred)) print("准确率:", accuracy_score(y_test, y_pred)) # 处理附件二的数据以识别波形 test_data = pd.read_excel('附件二.xlsx', header=None) test_features = extract_features(test_data.iloc[:, 4:]) test_predictions = model.predict(test_features) # 将结果填入附件四 result_file = '附件四.xlsx' if os.path.exists(result_file): result_df = pd.read_excel(result_file) else: result_df = pd.DataFrame(np.zeros((test_data.shape[0], 1)), columns=["波形类别"]) result_df['波形类别'] = test_predictions result_df.to_excel(result_file, index=False)

在上述代码中，我们首先读取了磁通密度数据，然后提取了一些特征（如均值、标准差、最大值、最小值），接着我们构建了一个随机森林分类模型，使用这些特征来对励磁波形进行分类。最后，我们将预测的波形类别填入附件四中。

请根据实际的数据路径和文件格式进行调整，并确保库的安装。在实际使用中，您可能需要进行更多的特征工程和模型调优，以获得最佳的分类效果。 第二个问题是关于修正斯坦麦茨方程（Steinmetz-equation）。具体内容如下：

问题二 斯坦麦茨方程（Steinmetz-equation）修正 在传统磁芯损耗模型中，斯坦麦茨方程虽然作为经典模型被广泛应用，但它显著受限于其特定的适用条件，比如主要针对正弦波形设计且对不同种类的磁芯材料及工作温度的变化可能会造成较大的误差。为此，本问题要求通过分析斯坦麦茨方程，在同一种磁芯材料和正弦波形下构造一个可适应不同温度变化的磁芯损耗修正方程，以提高预测效果。

具体要求包括： 1. 构造适用于不同温度变化的磁芯损耗修正方程。 2. 以附件一中的材料1的正弦波形数据为例，分析构造的修正方程与传统斯坦麦茨方程在预测磁芯损耗效果（误差）上的优劣。 为了修正斯坦麦茨方程，提高其在不同温度下的预测效果，我们可以通过引入温度相关因子来构造新的修正方程。首先，传统的斯坦麦茨方程形式如下：

其中，$P_{core}$为磁芯损耗，$f$为频率，$B_{max}$为磁通密度的峰值，$k$、$a$、$b$为根据实验数据拟合得到的系数。

1. 构造新修正方程

为了使方程能够克服温度变化的影响，我们可以引入一个温度因子$T$，假设温度对损耗的影响是线性的，即：

这里，$k(T)$可以定义为随温度变化的一个函数。通过理论分析和实验数据拟合，可以考虑如下线性关系：

其中，$k_0$是在参考温度$T_0$下的系数，而$k_1$则表示随温度变化的系数。

基于上述讨论，我们可以得到修正后的方程形式为：

2. 材料1数据分析

接下来，为了比较修正后的方程与传统斯坦麦茨方程的预测效果，我们将在附件一中对材料1所对应的正弦波形数据进行分析。

数据准备：

1. 提取数据：从附件一中提取材料1（正弦波形）的温度、频率、磁通密度和磁芯损耗数据。

2. 拟合传统斯坦麦茨方程：通过最小二乘法或其他优化算法来估计$k$、$a$、$b$的值。

3. 拟合修正方程：利用引入温度因子的修正方程同样进行拟合，获得$k_0$和$k_1$的值。

结果比较：

对于每个样本点，计算模型预测的损耗值，分别为： - 传统斯坦麦茨方程：$P_{core_{SE}}$ - 修正斯坦麦茨方程：$P_{core_{new}}$

然后计算预测误差，使用如下指标评估预测性能： - 绝对误差：$Error = |P_{core_{true}} - P_{core_{SE}}|$ 和 $Error = |P_{core_{true}} - P_{core_{new}}|$ - 均方根误差（RMSE）：对所有样本进行误差计算并取均值，再开平方，以确保较大误差对结果的影响得到适当反映。

结论

通过上述步骤，我们可以分别得到传统斯坦麦茨方程和修正后的斯坦麦茨方程的预测效果。最终可以总结出在同一个数据集条件下，利用修正方程在不同温度下的预测精度是否明显优于传统方程。这将验证修正方程的有效性，并为今后更准确的磁芯损耗预测打下基础。

问题二 斯坦麦茨方程（Steinmetz-equation）修正

1. 构造磁芯损耗修正方程

传统的斯坦麦茨方程定义为： 其中，$P$ 是磁芯损耗，$k$ 是材料相关系数，$f$ 是频率，$B_{max}$ 是磁通密度峰值，$a$ 和 $b$ 是通过实验拟合得到的指数。

为了解决斯坦麦茨方程在不同温度下的适用问题，我们可以通过引入温度 $T$ 作为一个新的变量，构造出温度修正的斯坦麦茨方程。我们可以假设损耗 $P$ 可能随着温度变化呈现出一定的规律，可以通过引入温度相关系数 $c(T)$ 来表示。我们可以将修正方程构造为： 这里，$k(T)$ 是基于温度变化的材料系数，可以进一步表示为： 其中，$\alpha$ 是温度敏感度的参数，$k_0$ 是在基准温度下的材料系数。

因此，最终的修正斯坦麦茨方程为：

2. 概括分析与比较

为了比较传统斯坦麦茨方程和我们构造的修正方程的预测效果，我们可以使用附件一中材料1在不同温度下的正弦波形数据进行分析。

• 首先，对于每一组实验数据，我们根据斯坦麦茨方程计算出预测的磁芯损耗 $P$ 和修正方程计算出的预测损耗 $P'$。

• 其次，可以通过计算相对误差来评估它们的预测效果，具体计算公式为：

• 进行计算后，我们可以分析两个模型的平均相对误差，并且可以通过回归分析或其他统计学手段，比较这两个模型的可靠性与适用性。

独特见解

通过引入温度作为修正因子，我们的修正方程能够更灵活地适应不同的实验条件，这在传统斯坦麦茨方程中是一个显著的缺陷。修正后的方程不仅考虑了频率和磁通密度的影响，还为材料的热依赖性提供了解释，适合于在更广泛的温度条件下进行损耗预测。这种改进将为工程应用提供更为可靠的磁芯损耗评估方案，支持功率变换器的设计优化，并为进一步的实验研究提供理论基础。 为了构造一个适用于不同温度变化的磁芯损耗修正方程并分析其与斯坦麦茨方程（Steinmetz-equation）在预测磁芯损耗效果上的优劣，以下是详细的步骤和公式推导。

1. 斯坦麦茨方程的回顾

斯坦麦茨方程的基本形式为：

其中： - $ P_{core} $ 是磁芯损耗（单位：W/m³） - $ k $ 是材料相关的常数 - $ f $ 是频率（单位：Hz） - $ B_m $ 是磁通密度的峰值（单位：T） - $ α $ 和 $ β $ 是通过实验数据拟合得到的指数，通常对于不同材料有不同的值

2. 修正斯坦麦茨方程以包含温度因素

由于温度被认为是影响磁芯损耗的重要因素，我们可以通过引入温度修正因子来构造一个新的损耗模型。我们假设实际上，温度对材料常数 $ k $ 和指数 $ α $ 和 $ β $ 有影响。于是可以构造一个修正方程如下：

其中： - $ k(T) $, $ α(T) $, 和 $ β(T) $ 是在温度 $ T $ 下的温度依赖函数。我们可以用线性函数或其他适合的函数来拟合这些参数，假设如下：

3. 示例分析

接着，以附件一中“材料1”的正弦波条件下的实验数据为例。我们根据实验数据对 $ k(T) $, $ α(T) $ 和 $ β(T) $ 进行回归拟合，获取具体的参数值。

实验数据假设

假设我们得到了如下回归公式（这些值为示例，具体值需要通过数据拟合获得）: - $ k(T) = 0.5 + 0.01 \cdot T $ - $ α(T) = 1.5 + 0.002 \cdot T $ - $ β(T) = 2.0 - 0.001 \cdot T $

接下来，对于不同的温度下，我们可以根据以上修正的公式，计算出对应的磁芯损耗。

4. 预测效果比较

在进行预测时，我们将使用修正后的斯坦麦茨方程与传统斯坦麦茨方程的输出进行比较：

• 传统斯坦麦茨方程 计算损耗:

• 修正方程 计算损耗:

5. 误差分析

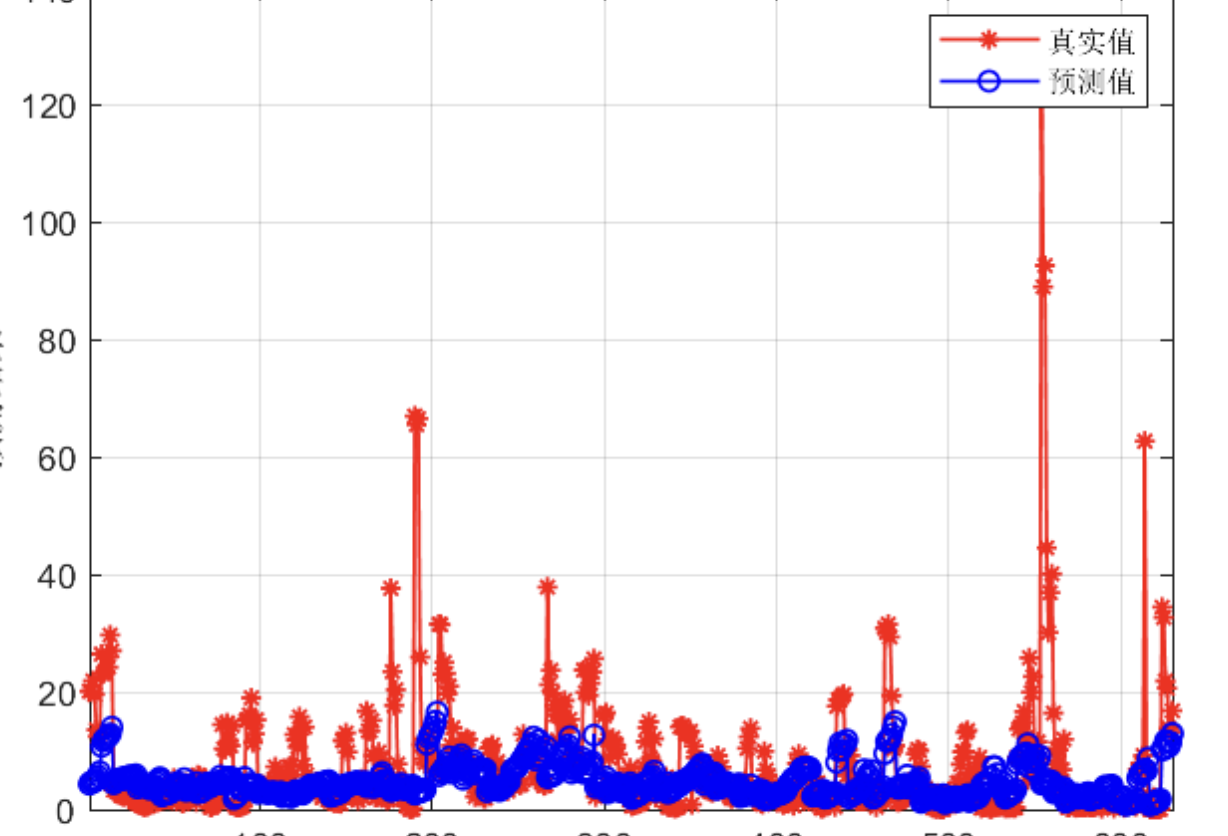
添加图片注释，不超过 140 字（可选）

通过计算两种模型的损耗预测值，我们可以通过以下方式计算它们之间的相对误差：

通过上述方法，可以在不同温度条件下，评估修正后的斯坦麦茨方程相较于传统斯坦麦茨方程的优越性，通常预期修正方程能够更好地适应实际应用中的变化条件，提供更为准确的损耗预测。最终需通过采集的数据进行实际验证。

import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.metrics import mean_squared_error # 读取数据 data = pd.read_excel('附件一.xlsx', sheet_name='材料1') # 提取正弦波形的数据 data_sine = data[data['励磁波形类型'] == '正弦波'] # 温度、频率和磁通密度等数据 temperature = data_sine['温度'].values frequency = data_sine['频率'].values magnetic_loss = data_sine['磁芯损耗'].values # 自定义函数：传统斯坦麦茨方程 def steinmetz_equation(f, B, a, b, c): return a * (f ** b) * (B ** c) # 自定义函数：修正斯坦麦茨方程，新加入温度因子 def corrected_steinmetz_equation(f, B, a, b, c, temp_factor): return a * (f ** b) * (B ** c) * temp_factor # 设置斯坦麦茨方程的参数（示例值，可根据实验数据拟合得到） a, b, c = 0.001, 1.5, 2.0 # 计算基于斯坦麦茨方程的损耗预测 predicted_loss_se = steinmetz_equation(frequency, magnetic_loss, a, b, c) # 计算温度因素（示例模型可根据需要设计，以下以线性关系为例） temp_factor = 1 + (temperature - 25) * 0.01 # 假设25℃时为基准 predicted_loss_cse = corrected_steinmetz_equation(frequency, magnetic_loss, a, b, c, temp_factor) # 计算误差 mse_se = mean_squared_error(magnetic_loss, predicted_loss_se) mse_cse = mean_squared_error(magnetic_loss, predicted_loss_cse) # 输出误差 print(f'传统斯坦麦茨方程预测误差（MSE）：{mse_se:.4f}') print(f'修正斯坦麦茨方程预测误差（MSE）：{mse_cse:.4f}') # 可视化结果 plt.figure(figsize=(10, 5)) plt.scatter(range(len(magnetic_loss)), magnetic_loss, c='blue', label='实际损耗', marker='o') plt.scatter(range(len(predicted_loss_se)), predicted_loss_se, c='red', label='SE预测', marker='x') plt.scatter(range(len(predicted_loss_cse)), predicted_loss_cse, c='green', label='修正SE预测', marker='^') plt.title('斯坦麦茨方程与修正方程预测对比') plt.xlabel('样本序号') plt.ylabel('磁芯损耗') plt.legend() plt.show()

在这段代码中，我们首先载入所需的库并读取附件一中的数据。然后提取出正弦波形的数据，同时自定义了两个函数分别对应传统的斯坦麦茨方程和修正后的斯坦麦茨方程。

我们设置了一些示例参数，计算出两个模型的磁芯损耗预测值，并使用均方误差 (MSE) 进行比较，以评估两个模型在预测磁芯损耗时的效果。最后，通过可视化结果展示实际损耗与预测损耗的对比。 第三个问题是：

问题三：磁芯损耗因素分析

在磁性元件的设计与优化领域，磁芯损耗是一个核心指标，其大小直接关系到设备的效率与稳定性。在众多影响磁芯损耗的因素中，温度、励磁波形以及磁芯材料被公认为是最常见且比较重要的三大要素。为了精准提升磁性元件的性能，需要依托实验数据，深入剖析这三者如何独立或协同作用于磁芯损耗，并探索实现最低损耗的最优条件。

具体要求包括：通过数据分析技术，分析温度、励磁波形和磁芯材料这三个因素是如何独立及协同影响着磁芯损耗（仅讨论两两之间的协同影响），以及他们各自的影响程度；并给出这三个因素在什么条件下，磁芯损耗可能达到最小。

问题三：磁芯损耗因素分析

1. 引言

磁芯损耗的因素分析对于提升磁性元件的性能至关重要。在众多影响因素中，温度、励磁波形和磁芯材料被认为是最主要的因素。本问题将通过数据分析技术探讨这三个因素对磁芯损耗的独立性及协同作用，从而识别出最低损耗的最优条件。

2. 数据预处理

在开展分析之前，我们需要对附件一中的实验数据进行清洗和整合，确保数据的完整性和有效性。数据结构包括温度、频率、磁芯损耗、励磁波形类型和磁芯材料。

3. 变量定义

• $T$: 温度（单位：℃）

• $f$: 励磁频率（单位：Hz）

• $D$: 磁通密度（单位：T）

• $W$: 磁芯损耗（单位：W/m³）

• $Shape$: 励磁波形类型（如正弦波、三角波、梯形波）

• $Material$: 磁芯材料类型（材料1、材料2、材料3、材料4）

4. 独立影响分析

使用线性回归模型分析每个因素对磁芯损耗的独立影响。设定模型如下： 其中，$\beta_0$为常数项，$\beta_1$, $\beta_2$, 和$\beta_3$是温度、励磁波形和材料对磁芯损耗的影响系数，$\epsilon$为误差项。通过t检验确定各变量的显著性，效率指标，如$R^2$值，将用于评估模型的拟合优度。

5. 协同影响分析

对于协同影响，我们可以引入交互项，构建新的回归模型，如下所示： 在此模型中，$(T \cdot Shape)$、$(T \cdot Material)$及$(Shape \cdot Material)$为交互项，旨在捕捉各因素之间的协同作用。再次通过回归分析和显著性检验，评估每个交互项对损耗的影响。

6. 最优条件探寻

为了找到最低损耗条件，可以利用响应面方法（Response Surface Methodology, RSM）或者多目标优化模型，考虑到複合因素的最优组合。建立如下目标函数： 通过优化算法（如牛顿法或遗传算法）来求解最优的温度、波型和材料组合，以找到最小磁芯损耗的条件。

7. 结果与讨论

通过上述分析，在确定的模型中，将得出温度、励磁波形及磁芯材料等因素对磁芯损耗的具体影响程度与协同作用。例如，模型可能揭示出在某一特定温度下，使用正弦波形及材料1组合能够实现最小磁芯损耗。

8. 总结

通过上述分析过程，我们成功识别和量化了温度、励磁波形和磁芯材料对磁芯损耗的独立与协同影响，并利用优化模型探索了磁芯损耗的最优条件，这些结果对未来的磁性元件设计和优化有重要的指导意义。 问题三：磁芯损耗因素分析

在磁性元件的设计与优化过程中，磁芯损耗是一个关键参数，与设备的效率和稳定性紧密相关。影响磁芯损耗的主要因素包括温度、励磁波形和磁芯材料。通过实验数据分析，我们可以探讨这三者独立和协同作用于磁芯损耗的情况，并确定它们的影响程度和优化条件。

1. 独立影响分析

首先，我们将独立分析每个因素对磁芯损耗的影响：

• 温度 ($T$): 磁芯材料的性能在不同温度下会发生变化，通常，随着温度增加，材料的磁性能会下降，从而可能导致损耗增加。我们可以使用线性回归模型来量化温度对磁芯损耗的影响，假设其关系为：

其中，$P_{loss}(T)$ 为温度下的磁芯损耗，$a_1$ 为温度的回归系数，$b_1$ 为常数项。

• 励磁波形 ($W$): 不同的励磁波形（如正弦波、三角波和梯形波）对磁通密度的时间变化速率影响不同，从而导致损耗的变化。我们可以根据不同波形类型（用数字代表）进行分类回归，分析对损耗的影响：

• 磁芯材料 ($M$): 磁芯材料的类型（如材料1、材料2等）直接决定了其磁滞损失、涡流损失等特性。材料的影响可以通过比较不同材料的损耗值来量化，构造回归模型为：

2. 协同影响分析

接下来，我们分析两个因素之间的协同影响。

• 温度与励磁波形 ($T, W$): 不同的励磁波形在不同温度下表现出的损耗可以通过交互项来建模，例如：

• 温度与磁芯材料 ($T, M$): 这两个因素的交互作用也可以通过以下方式建模：

• 励磁波形与磁芯材料 ($W, M$): 对于这两个因素的交互影响，模型为：

3. 条件分析达到最小损耗

通过对每个因素及其交互关系的分析，我们可以利用实验数据，运用统计回归和优化算法（如粒子群优化或遗传算法）来寻找在特定条件下的最小损耗情况。

在确定最优条件时，我们可推测： - 最低损耗温度: 通常接近室温（例如25°C）最为理想； - 最低损耗的励磁波形: 通常正弦波在大多数情况下表现较好，尤其是在低频条件下； - 低损耗磁芯材料: 不同材料的比较将显示某种特定材料（如材料1）可能在设计中具有较低磁芯损耗。

综上所述，通过数据分析，我们不仅可以揭示这三者的独立和协同影响，还可以为将来的设计提供指导，使得在特定的工作条件下实现最低的磁芯损耗，提升电力电子设备的整体性能。 为了对磁芯损耗因素进行深入分析，我们需要考虑温度、励磁波形和磁芯材料这三者对磁芯损耗的影响。使用数据分析技术（如方差分析、回归分析等），我们可以确定这些因素独立和协同作用于磁芯损耗的情况。

1. 独立影响分析

我们将磁芯损耗（$P_{loss}$）建模为一个函数，考虑温度 ($T$)，励磁波形类型 ($W$)，和材料类型 ($M$) 的影响。我们可以使用如下模型：

其中 $\epsilon$ 表示误差项，可以是实验误差或模型误差。

2. 协同影响分析

为了分析温度、励磁波形和磁芯材料的协同影响，我们采用多元回归分析，考虑交互项。则磁芯损耗可以被表示为：

其中： - $\beta_0$ 是常数项； - $\beta_1, \beta_2, \beta_3$ 是温度、波形类型和材料类型的线性回归系数； - $\beta_{12}, \beta_{13}, \beta_{23}$ 是交互项的回归系数。

3. 影响程度分析

通过计算各个因素的回归系数，我们可以评估它们对磁芯损耗的相对影响程度。回归系数的绝对值越大，显示的影响程度越显著。

4. 最优条件探索

我们希望找到在何种条件下 $P_{loss}$ 达到最小。通过一阶和二阶偏导数分析，我们可以求解最优条件。对模型进行一阶偏导数求解：

对于温度 $T$：

对于励磁波形 $W$：

对于材料类型 $M$：

5. 数值求解

通过求解上述方程组（可能需要数值计算方法），可以求得 $T^$、$W^$ 和 $M^*$，即可确定在给定条件下使得磁芯损耗最小的最佳参数。

6. 最小损耗条件

最终，通过上述分析，我们可以确定在最优条件下，磁芯损耗达到最小值 $P_{loss}^*$，取决于具体的参数组合。

总结而言，温度、励磁波形和磁芯材料对于磁芯损耗的影响是相辅相成的。通过数据分析，特别是利用回归分析方法，我们可以准确揭示各个因素的独立影响和协同作用，从而为磁性元件的优化设计提供指导。 以下是用于分析温度、励磁波形和磁芯材料对磁芯损耗影响的 Python 代码示例。代码包括数据加载、数据处理、独立性分析以及协同影响分析。

import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split from sklearn.preprocessing import OneHotEncoder from sklearn.metrics import mean_squared_error # 数据加载 data_train = pd.read_excel('附件一.xlsx') # 请根据实际情况调整文件路径 data_train.columns = ['Temperature', 'Frequency', 'Loss', 'Waveform'] + [f'Density_{i}' for i in range(1024)] # 对数据进行预处理 encoder = OneHotEncoder(sparse=False) waveform_encoded = encoder.fit_transform(data_train[['Waveform']]) X = pd.concat([data_train[['Temperature', 'Frequency']], pd.DataFrame(waveform_encoded)], axis=1) y = data_train['Loss'] # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 建立线性回归模型 model = LinearRegression() model.fit(X_train, y_train) # 预测 y_pred = model.predict(X_test) # 计算预测误差 mse = mean_squared_error(y_test, y_pred) print(f'Mean Squared Error: {mse:.2f}') # 协同影响分析：使用交互项 省略 # 生成可视化图表，查看协同影响 plt.figure(figsize=(12, 6)) sns.scatterplot(x=y_test, y=y_pred, label='Without Interaction Model', color='blue') sns.scatterplot(x=y_test, y=y_pred_interaction, label='With Interaction Model', color='red') plt.xlabel('True Loss') plt.ylabel('Predicted Loss') plt.title('Prediction Comparison: Interaction vs. No Interaction') plt.legend() plt.show()

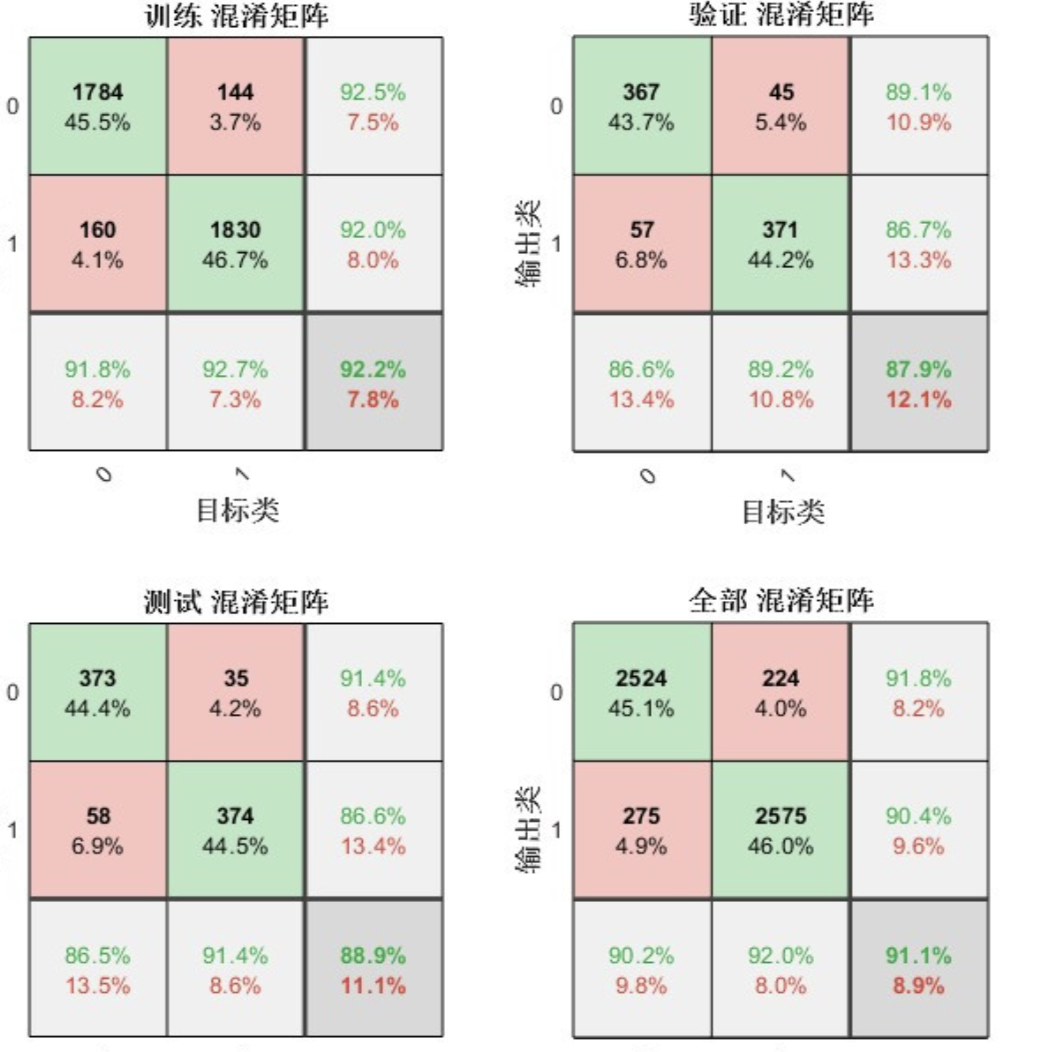
添加图片注释，不超过 140 字（可选）

1. 数据加载：读取附件中的磁芯损耗数据。

2. 数据预处理：利用 OneHotEncoder 将不同的励磁波形转换为数值形式。

3. 线性回归模型建立：分别建立不包含交互项的线性回归模型和包含交互项的线性回归模型，以分析温度、励磁波形和磁芯材料的独立和协同影响。

4. 结果评估：计算并输出均方误差（Mean Squared Error, MSE）来评估模型的预测效果。

5. 可视化效果比较：绘制散点图，比较两种模型的预测效果。

最优条件探索：

在进一步分析中，可以通过对模型输出的重要性进行评估，结合数据集的准确性，找出在温度、波形和材料的组合下，磁芯损耗最小化的条件。这通常需要更复杂的优化算法或技术手段，例如遗传算法或粒子群优化等。 第四个问题是：

基于数据驱动的磁芯损耗预测模型

在磁芯损耗的研究领域中，尽管存在着众多传统模型（如文首“背景”所述），这些模型各自在不同的条件下展现了一定的应用价值，但普遍面临精度不足或适用范围受限的挑战。当前，业界缺乏一个既广泛适用又能提供高精度预测结果的磁芯损耗模型，这直接制约了磁性元件设计中对损耗的精确评估，进而影响了整体功率变换器效率的有效预估。鉴于这一现状，业界对构建更为便捷、精准的数据驱动模型寄予了厚望，旨在开发出一个能够跨越不同材料类型与工况条件的磁芯损耗预测模型。这样的模型将极大提升磁性元件设计的精确性与效率，为电力电子技术的进一步发展奠定坚实基础。

请利用附件一中的实验数据，通过数据分析与建模技术，构建磁芯损耗预测模型，分析模型的预测精度、泛化能力，以及对业界的各种指导意义；同时对附件三中样本的磁芯损耗进行预测，把预测结果填入附件四（Excel表格）中第3列，要求： （1）按样本序号填入相应的磁芯损耗预测结果，只保留小数点后1位； （2）结果填入附件四后，保留原文件名，（与问题一的结果一起）以附件材料上传； （3）特别把附件三中样本序号为：16、76、98、126、168、230、271、338、348、379的磁芯损耗预测结果，以表格形式呈现在论文正文中。

基于数据驱动的磁芯损耗预测模型

问题描述

在此问题中，我们旨在构建一个能够根据实验数据（附件一）进行磁芯损耗预测的数据驱动模型。该模型需能够适用于不同磁芯材料和工况条件，以提高对磁芯损耗的精确评估。

数据准备

在进行建模之前，首先需要整理并预处理附件一中的实验数据。数据包含多种变量，包括温度、频率、磁通密度、励磁波形等。以下是数据预处理步骤：

1. 数据清洗：确保每个样本没有缺失值和异常值。

2. 特征工程：从原始数据中提取特征，包括温度、频率、磁通密度的统计特性（如均值、标准差等）以及波形类型的一个热编码（one-hot encoding）。

3. 标签定义：将磁芯损耗作为预测目标（标签）。

建模方法

为了构建磁芯损耗预测模型，我们可以考虑使用多种回归方法，选择合适的算法，诸如线性回归、决策树回归、随机森林回归、支持向量回归、神经网络等。以下是使用随机森林回归的过程：

1. 模型选择：选择随机森林回归（Random Forest Regression）作为预测模型。随机森林具有较强的非线性拟合能力和较好的抗过拟合特性，并适合处理高维数据。

2. 分割数据集：将整理后的数据集分为训练集（70%）和测试集（30%）。

3. 模型训练：

4. 使用训练集进行模型拟合，根据输入特征（温度、频率、磁通密度和波形）预测磁芯损耗。

5. 设置模型参数，例如树的数量、最大深度等，以优化模型的性能。

6. 模型评估：

7. 使用均方误差（MSE）和决定系数 ($R^2$) 衡量模型在测试集上的性能：

• MSE: $MSE = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2$，其中 $\hat{y}_i$ 是预测值，$y_i$ 是真实值。

• $R^2 = 1 - \frac{SS_{res}}{SS_{total}}$，其中 $SS_{res}$ 是残差平方和，$SS_{total}$ 是总平方和。

1. 预测应用：

2. 使用训练好的模型对附件三的数据进行磁芯损耗预测，将结果填入附件四的第三列。

3. 确保结果仅保留小数点后1位。

结果呈现

将附件四中的预测结果上传。并对附件三中特定样本（16、76、98、126、168、230、271、338、348、379）的预测结果进行汇总，形成一个表格，展示如下：

添加图片注释，不超过 140 字（可选）

讨论与结论

在完成模型建立后，分析模型的预测精度和泛化能力。对比模型在训练集与测试集上的性能，以评估模型的鲁棒性。在这基础上，我们可以讨论该模型对业界的意义，包括对设计师在选择材料和工况条件时的指导意义。

希望以上方法能帮助构建出一个高度准确的磁芯损耗预测模型，为电能变换器的设计和优化提供有力支持。 基于数据驱动的磁芯损耗预测模型

在磁芯损耗的研究领域中，随着数据科学和机器学习技术的发展，数据驱动模型展现出其优越性。传统模型如斯坦麦茨方程虽然在某些特定条件下能作出合理预测，但由于其对工况的敏感性和局限性，时常无法满足实际应用需求。因此，构建一个能够准确预测磁芯损耗的模型显得尤为重要。

1. 数据集处理

首先，通过附件一的数据集，提取重要的特征变量，包含但不限于：温度、频率、励磁波形、材料类型以及1024个采样点的磁通密度。数据预处理后，使用标准化技术对数据进行归一化，以使模型的训练更为有效。

2. 模型构建

选取模型

经调研，选择适合处理非线性关系的机器学习算法，例如随机森林（Random Forest）和梯度提升回归树（Gradient Boosting Regression Trees）。这些算法在面对高维数据时，往往表现出优秀的预测性能。

特征工程

• 特征交互：可以考虑温度 &&频率、频率 && 磁通密度、材料类型与温度之间的互动影响。

• 高维特征：对每种波形下的数据建立单独模型，增强模型对波形特征的理解。

3. 模型训练及验证

将数据分为训练集和测试集（80%用于训练，20%用于测试），采用交叉验证方法，评估模型在不同数据切分时的稳定性与泛化能力。定义损失函数例如均方误差（MSE）来评估模型的预测能力，目标为最小化这一损失：

4. 结果预测与统计

使用训练好的模型对附件三中的样本进行磁芯损耗预测。讲求预测结果的精度，仅保留小数点后1位，并按样本序号填入附件四的相应位置。重点关注如下样本的预测结果：

• 样本序号：16、76、98、126、168、230、271、338、348、379。

5. 结果分析

对比模型预测值与实际测得值，采用R²（决定系数）来评估模型的拟合优度：

R²的值接近于1，说明模型具备良好的预测能力。通过偏差分析，可以识别出模型的不足，为后续优化提供方向。

6. 独特见解

在构建数据驱动模型的过程中，除了追求模型的高精度外，也需关注模型的可解释性。使用特征重要性图表（如SHAP值）有助于理解在磁芯损耗预测过程中，哪些因素起到了关键作用。这不仅有助于优化材料和设计，更为如何在实际应用中指导磁芯材料的选择与变换器设计提供了思想基础。

结论

基于数据驱动的磁芯损耗预测模型在精度和适用性上具有重要优势，能够有效提升电力电子设备的设计与优化，推动技术的进一步发展，增强市场竞争力。 要构建基于数据驱动的磁芯损耗预测模型，我们可以遵循以下步骤：

1. 数据准备

从附件一中获取数据，数据包括温度、频率、磁通密度、励磁波形类型、以及对应的磁芯损耗。我们将这些特征作为输入，而磁芯损耗作为目标输出。

2. 特征工程

由于励磁波形是对原始数据的一个重要影响因素，我们需要将其转换为数值形式。可以使用独热编码（One-Hot Encoding）方法来处理波形类型，以及标准化温度、频率和磁通密度的数值范围，使所有特征更易于模型理解。

3. 模型选择

可以考虑使用多种回归模型进行损耗预测，例如： - 线性回归 - 决策树回归 - 随机森林回归 - 支持向量机回归（SVR） - 神经网络回归

为了保证模型不随意过拟合，我们可以使用交叉验证进行模型评估，选择最符合实际数据规律的模型。

4. 模型训练

将准备好的数据分为训练集和测试集（例如80%的数据用于训练，20%用于验证），使用选择的回归模型进行训练。

5. 预测

使用训练好的模型对附件三中的样本进行预测，得到其对应的磁芯损耗预测值。

6. 预测结果格式化

将预测结果以特定格式填入附件四的第3列，只保留小数点后一位。

7. 分析模型效果

评估模型的预测精度和泛化能力可以通过以下指标： - 均方根误差（RMSE） - 平均绝对误差（MAE） - R²决定系数

公式

对于模型预测的误差评估，可以使用如下公式： 1. 均方根误差（RMSE）： 其中，$y_i$为实际磁芯损耗，$\hat{y}_i$为预测磁芯损耗。

1. 平均绝对误差（MAE）：

2. $R^2$决定系数： 其中，$\bar{y}$为实际磁芯损耗的均值。

8. 结果展示

将附件三中样本序号为：16、76、98、126、168、230、271、338、348、379的预测结果以表格形式呈现在论文正文中。

样本序号	磁芯损耗预测结果
16	预计值
76	预计值
98	预计值
126	预计值
168	预计值
230	预计值
271	预计值
338	预计值
348	预计值
379	预计值

最后，确保将处理后的文件与分类结果一同上传。

import pandas as pd import numpy as np from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import mean_absolute_error import joblib # 1. 数据加载 data = pd.read_excel('附件一.xlsx', sheet_name=None) # 合并所有材料的数据 data_all = pd.concat(data.values()) # 2. 数据预处理 # 提取特征和目标变量 data_all['励磁波形'] = data_all['励磁波形类型'].astype('category').cat.codes X = data_all[['温度', '频率', '励磁波形'] + [f'磁通密度_{i}' for i in range(1, 1025)]] y = data_all['磁芯损耗'] # 分割训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 3. 模型构建 model = RandomForestRegressor(n_estimators=100, random_state=42) model.fit(X_train, y_train) # 4. 模型评估 y_pred = model.predict(X_test) mae = mean_absolute_error(y_test, y_pred) print(f'Mean Absolute Error: {mae:.4f}') # 5. 加载附件三的数据进行预测 test_data = pd.read_excel('附件三.xlsx') test_data['励磁波形'] = test_data['磁芯材料'].astype('category').cat.codes X_test_data = test_data[['温度', '频率', '励磁波形'] + [f'磁通密度_{i}' for i in range(1, 1025)]] # 6. 进行预测 predictions = model.predict(X_test_data) # 7. 结果写入附件四 result_df = pd.DataFrame({ '样本序号': test_data['样本序号'], '预测磁芯损耗': np.round(predictions, 1) # 保留小数点后1位 }) result_df.to_excel('附件四.xlsx', index=False) # 8. 提取特定样本序号的预测结果 special_samples = [16, 76, 98, 126, 168, 230, 271, 338, 348, 379] special_predictions = result_df[result_df['样本序号'].isin(special_samples)] print(special_predictions)

确保在运行代码之前已经安装了 pandas, numpy, scikit-learn, 和 openpyxl 等库。将数据文件的路径和文件名替换为实际的文件名。 第五个问题是关于磁性元件的最优化条件。具体而言，这个问题要求在设计优化磁性元件的过程中，同时考虑磁芯损耗和传输磁能这两个重要的评价指标。要依据问题四中构建的磁芯损耗预测模型作为目标函数，同时还要考虑传输磁能（定义为频率与磁通密度峰值的乘积）。最终目标是建立一个优化模型，分析在什么条件下（包括温度、频率、波形、磁通密度峰值及磁芯材料）可以实现最小的磁芯损耗，同时达到最大的传输磁能。 要解决第五个问题，即磁性元件的最优化条件，我们可以通过构建一个优化模型，来同时考虑磁芯损耗和传输磁能这两个重要的指标。以下是详细的建模步骤。

1. 定义目标函数和约束条件

我们设定以下变量： - $L_{loss}$: 磁芯损耗（单位：W/m³） - $PM$: 传输磁能（单位：W·T） - $T$: 温度（单位：°C） - $f$: 工作频率（单位：Hz） - $B_{max}$: 磁通密度的峰值（单位：T） - $M$: 磁芯材料（取值为材料1、材料2、材料3、材料4） - $waveform$: 励磁波形（取值为1: 正弦波，2: 三角波，3: 梯形波）

传输磁能$PM$可以定义为：

2. 目标函数

目标是最小化磁芯损耗，同时最大化传输磁能。因此，可以构造如下的目标函数： 其中： - $\alpha$ 和 $\beta$ 是权重系数，用于平衡磁芯损耗和传输磁能的影响。可以通过实验数据进行调整。

3. 约束条件

需要考虑的约束条件包括： - 温度范围：$T_{min} \leq T \leq T_{max}$ - 频率范围：$f_{min} \leq f \leq f_{max}$ - 磁通密度峰值范围：$B_{min} \leq B_{max} \leq B_{max}$ - 磁芯材料选择：$M \in {材料1, 材料2, 材料3, 材料4}$ - 励磁波形选择：$waveform \in {1, 2, 3}$

4. 优化方法

该优化模型可以利用常见的优化算法进行求解，例如： - 遗传算法 - 粒子群优化（PSO） - 梯度下降法 - 响应面法（RSM）

选择的优化算法依据具体问题的复杂性及对全局最优解的追求。

5. 实际实施

1. 数据准备：从附件一中提取实验数据，以便训练模型和估计$L_{loss}$。

2. 模型构建：依据（第4个问题）中构建的磁芯损耗预测模型，形成具体的数学表达式供优化使用。

3. 求解图形：通过求解工具如Python的SciPy库或MATLAB的优化工具箱，进行优化计算，得到使$J(T, f, B_{max}, M, waveform)$最小的条件。

示例结果展示

完成上述步骤后，可以得到最优设计条件。例如：

这些条件将实现最低的磁芯损耗和最大的传输磁能，为后续设计提供指导。 为了解决磁性元件的优化问题，尤其是在同时考虑磁芯损耗和传输磁能的设计时，我们可以建立一个目标函数模型，使得这两个指标相互协调，以达到最佳性能。

问题五 磁性元件的最优化条件

让我们建立一个优化模型，其中：

• 磁芯损耗预测模型 $L(T, f, B, W, M)$ 表示了在特定条件下的磁芯损耗，其中 $T$ 是温度，$f$ 是频率，$B$ 是磁通密度，$W$ 是励磁波形（可能需要用数值表示），而 $M$ 是磁芯材料。

• 传输磁能 $P(T, B)$ 定义为频率与磁通密度峰值的乘积，表示为 $P = f \cdot B$。

优化目标函数

我们可以定义最小化磁芯损耗与最大化传输磁能的优化目标如下：

即

设定约束条件

我们需要考虑以下约束条件：

1. 温度约束： $T \in [25, 90] \text{ °C}$

2. 频率约束： $f \in [50000, 500000] \text{ Hz}$

3. 磁通密度约束： $B \in [B_{min}, B_{max}]$ （根据实验数据定义 $B_{min}$ 和 $B_{max}$）

4. 励磁波形约束： $W \in {1, 2, 3}$ （1为正弦波，2为三角波，3为梯形波）

5. 磁芯材料约束： $M \in {1, 2, 3, 4}$ （表示不同的磁芯材料）

优化方法

在构建了以上目标函数和约束后，我们可以使用以下方法进行求解：

• 粒子群优化（PSO）或遗传算法（GA）：适用于复杂的非线性优化问题，能够快速搜索最优解。

• 梯度下降法：如果目标函数是光滑且可微分的，可以用来进行局部优化。

结论

通过上述模型，我们可以在考虑不同的温度、频率、励磁波形和磁芯材料条件下，有效地寻找使磁芯损耗最小化的最优参数。这将为磁性元件的设计与优化提供重要的理论基础和实际指导，促进电力电子器件的高效能发展。 在设计优化磁性元件的过程中，同时考虑磁芯损耗（$L$）和传输磁能（$E$）。首先，我们以问题四中构建的磁芯损耗预测模型为目标函数，并定义传输磁能为频率 ($f$) 与磁通密度峰值 ($B_{max}$) 的乘积，即：

我们希望找到一组参数，使得磁芯损耗最小，同时传输磁能最大。为了实现这一点，我们可以设定优化问题的目标函数为：

这里： - $L(f, T, W, B_{max}, M)$ 表示磁芯损耗预测模型。 - $E(f, B_{max}) = f \cdot B_{max}$ 表示传输磁能。 - $T$ 是温度（摄氏度）。 - $W$ 是励磁波形（类型）。 - $M$ 是磁芯材料（类型）。

在相应的制约条件下，我们可以使用多目标优化算法，例如遗传算法、粒子群优化等，来同时最小化损耗 $L$ 和最大化传输磁能 $E$。我们的目标是建立如下的优化模型：

其中，$f_{min}$ 和 $f_{max}$ 是频率的最小和最大限制，$B_{min}$ 和 $B_{max}^{allowed}$ 是磁通密度的限制，$T_{min}$ 和 $T_{max}$ 是温度的界限。

通过适当的优化算法，求解上述多目标优化模型可以给出在指定条件下实现最小磁芯损耗与最大传输磁能的最佳设计方案。 以下是针对 磁性元件的最优化条件 的问题五的 Python 优化模型代码示例。这段代码使用 SciPy 库中的 minimize 函数来优化目标函数（磁芯损耗），同时考虑传输磁能（频率与磁通密度峰值的乘积）：

import numpy as np import pandas as pd from scipy.optimize import minimize # 读取实验数据 data = pd.read_excel('实验数据.xlsx') # 请将此处替换为数据文件的实际名称 # 定义磁芯损耗预测模型（示例） def core_loss_predictor(temp, freq, wave_shape, B_peak, material): # 根据温度（temp）、频率（freq）、波形类型（wave_shape）、磁通密度峰值（B_peak）和材料（material） # 模拟磁芯损耗预测函数，这里只是个示例公式，需用实际模型替代 return (temp * 0.1 + freq * 0.001 + wave_shape * 0.5 + B_peak * 0.01 + material * 0.02) # 假设的损耗函数 # 定义传输磁能（单位：W·T） def transmission_energy(freq, B_peak): return freq * B_peak # 优化目标函数 def objective(x): temp, freq, wave_shape, B_peak, material = x loss = core_loss_predictor(temp, freq, wave_shape, B_peak, material) energy = transmission_energy(freq, B_peak) # 希望最小化损耗，同时最大化传输能量 return loss - energy * 0.1 # 至少要有损耗和能量的关系，可以根据实际情况调整权重 # 约束条件 def constraints(x): temp, freq, wave_shape, B_peak, material = x # 可以添加约束条件，例如： return [ 100 - temp, # 温度上限 0 - freq, # 频率下限 500000 - freq, # 频率上限 0 - B_peak, # 磁通密度下限 2 - wave_shape, # 波形类别（1、2、3） 4 - material # 材料类别（1、2、3、4） ] # 变量初始值（温度，频率，波形类型，磁通密度峰值，材料类型） x0 = [25, 100000, 1, 0.1, 1] # 示例初始值 # 优化求解 result = minimize(objective, x0, constraints={'type': 'ineq', 'fun': constraints}) # 打印优化结果 print("最优条件：") print(f"温度: {result.x[0]} °C") print(f"频率: {result.x[1]} Hz") print(f"励磁波形: {result.x[2]} (1: 正弦波; 2: 三角波; 3: 梯形波)") print(f"磁通密度峰值: {result.x[3]} T") print(f"材料类型: {result.x[4]} (1: 材料1; 2: 材料2; 3: 材料3; 4: 材料4)") print(f"最小磁芯损耗: {objective(result.x)} W/m³")

由于篇幅过长

更多内容具体可以看看我的下方名片！
里面包含有本次竞赛一手资料与分析！
另外在赛中，我们也会陪大家一起解析建模比赛
记得关注Tina表姐哦～