2024年华为杯研赛（E题）｜高速公路应急车道启用建模｜数学建模竞赛解题思路|完整代码论文集合

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次研赛（6题）完整内容均可以在文章末尾领取！（部分代码在本帖子里格式混乱，下载后格式正常）

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。

本次研赛E题可以做如下考虑

添加图片注释，不超过 140 字（可选）

问题一主要涉及如何利用四个视频观测点的数据来进行交通流的分析和建模，具体包括三个小问：

1. 针对四个观测点的交通流参数，统计它们随时间的变化规律，以便未来建模。

2. 建立一个交通流拥堵模型，根据四个观测点的基本参数（如车流密度、流量、速度等）和道路情况，提供实时预警，预测在第三点到第四点之间可能发生的持续拥堵状态。

3. 利用视频数据对所建立的交通流拥堵模型进行有效性验证。

这三个小问旨在分析和监测交通流动态，并为实时交通管理提供依据，以避免道路拥堵的发生。 第一个问题主要涉及对交通流数据的分析与建模，以下是对该问题的详细解答，分为三个小问。

（1）统计四个观测点的交通流参数随时间的变化规律

添加图片注释，不超过 140 字（可选）

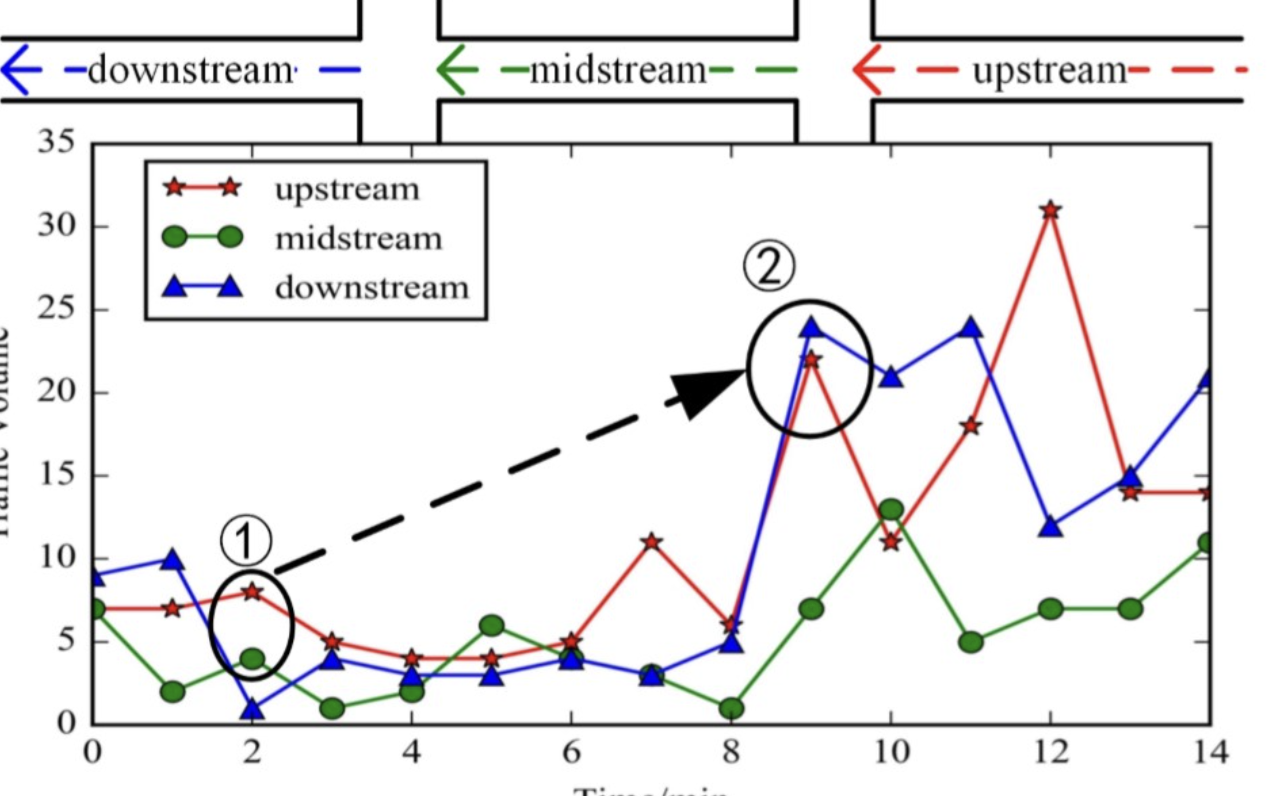
添加图片注释，不超过 140 字（可选）

（2）建立交通流拥堵模型，提供实时预警

我们可以依据基本的交通流理论建立一个拥堵模型。一个常用的模型是基于一种简单的流量-密度关系，例如 Greenshields 模型：

Q=K⋅V

由于交通流可能出现拥堵，需要建立与拥堵相关的状态检测条件。可以定义临界密度 $ K_{c} $，一旦实际密度 $ K $ 达到这个值时，即可认为路段存在拥堵风险。

1. 实时监测：

2. 在观测点 $ P_3 $ 和 $ P_4 $ 处，如果在过去的 10 分钟内，流量 $ Q $ 持续小于某个阈值（例如 800 veh/h），并且密度 $ K > K_{c} $，则发出拥堵预警。

3. 持续拥堵判断：

4. 如果在该路段的车流形成的密度持续大于 $ K_{c} $ 的时间超过30分钟，则可以判定为“持续拥堵”（可用公式表示为）

上面的公式用于判断在警示时间前是否可能发生持续拥堵。

（3）利用视频数据验证所建模型的有效性

最后，结合视频数据来验证模型预测的准确性，可以通过以下步骤进行：

1. 数据收集：从四个视频监测点获取实际的交通流量、速度和密度数据。

2. 模型输出对比：将以上模型的预测结果与视频观察到的实际交通流参数进行对比，通过时间序列分析计算模型的误差：

1. 明确指标：使用真实车流图像监控的数据，对关键时期的拥堵发生情况进行标记，并计算预测的准确率和灵敏度。

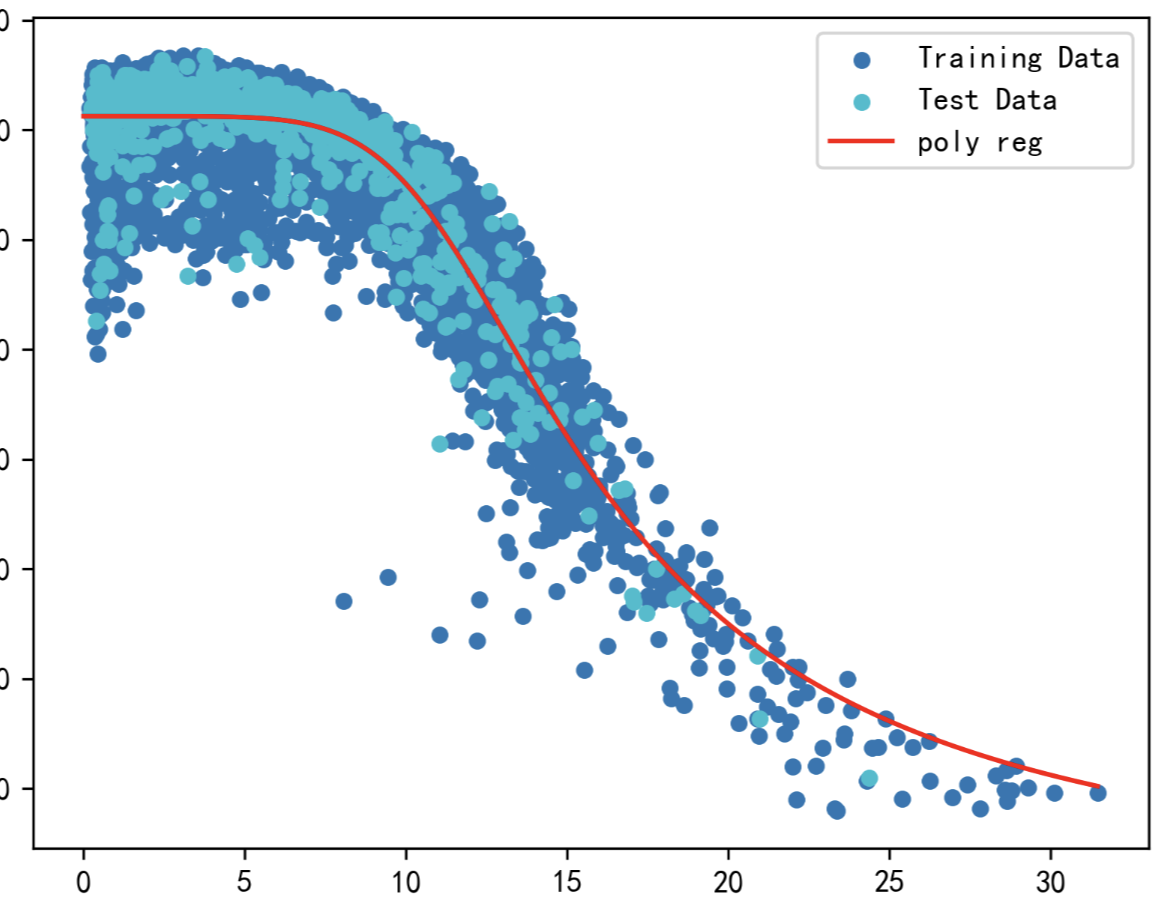
添加图片注释，不超过 140 字（可选）

以上步骤通过系统的数据收集、动态监测和有效模型构建，旨在为高速公路交通流管理提供科学依据，以在出现拥堵之前发出预警，最大限度地优化道路资源的利用。

利用四个视频观测点的数据进行交通流分析与建模

（1）交通流参数统计

针对四个观测点的交通流参数（车流密度、流量、速度）的变化规律，我们可以在以下几个方面进行统计分析：

1. 车流密度 ($D$)：车流密度是单位长度道路上的车辆数，可通过视频监控数据计算得到。假设每个观测点在时间$t$内记录到的车辆数为$N_t$，则车流密度可以表示为： 其中，$L$为单位长度（通常为100米或200米）。

2. 流量 ($Q$)：流量是单位时间内通过某一点的车辆数，通常以车辆/小时计。在每个观测点一定时间段内 ($\Delta t$) 的流量可以计算为： 其中，$N_{\Delta t}$为在时间$\Delta t$内经过观测点的车辆总数。

3. 速度 ($V$)：车速通常可通过流量和密度的关系来推导。根据基本的交通流理论，流量、速度和密度之间的关系为： 由此，我们可以求得速度： 通过对四个观测点在不同时段的数据收集，我们可以分析这些参数随时间的变化趋势。

（2）交通流拥堵模型

为了建立交通流拥堵的预测模型，我们可以采用基于连续监测数据的动态系统模型。设定以下参数：

• $D_i(t)$：观测点$i$在时间$t$的车流密度

• $Q_i(t)$：观测点$i$在时间$t$的车流量

• $V_i(t)$：观测点$i$在时间$t$的车速

我们可以利用以下模型来预测未来的拥堵状态。对于需要预警的条件，我们可以设定：

1. 当观测点3到观测点4的车流密度超过某一预设阈值（例如$D_{threshold}$），同时流量低于某一临界值（例如$Q_{low_threshold}$），则可以预测将会出现拥堵：

2. 持续时间和提前预警时间的设定：可以设定持续监控时间，例如持续时间为$t=30$分钟，并在预测出现拥堵的10分钟前进行预警。

（3）模型的有效性验证

为了验证所建立的交通流拥堵模型有效性，我们可以进行以下步骤：

1. 数据比对：将模型预测的拥堵时间与实际监控视频中观察到的拥堵时间进行比对，利用交叉验证法评估模型的准确性。

2. 统计分析：使用统计量（如均方根误差 RMSE、绝对误差等）对模型的预测结果与实际结果进行定量分析，以评估模型的性能。

3. 时间序列分析：利用时间序列的自相关和交叉相关分析，验证不同观测点之间的车流状态是否有一致性。

通过以上方法，我们可以初步分析和预测交通流动态，为实时交通管理提供有效的决策依据，减少道路拥堵的可能性。 针对第一个问题，我们将详细讨论如何利用四个视频观测点的数据进行交通流参数的分析和建模。以下是针对三个小问的具体解答：

(1) 统计交通流参数随时间的变化规律

交通流参数包括车流密度（$k$）、流量（$q$）和速度（$v$）。可以通过视频监测每个观测点的数据，计算上述参数随时间的变化规律。

• 车流密度 $k$： 其中 $N$为单位时间内通过观测点的车辆数量，$L$为观测段的长度（可设定为100米，比如：$L = 100 m$）。</