强化学习（一）：强化学习与马尔科夫决策过程

1. 强化学习概念

1.1. 负反馈控制

在经典的自动控制原理中，控制信号$u$是根据被控对象的状态进行控制的，同时再考虑被控量的理想值，最终能使被控量的实际值 和 理想值达到一致。

这样的控制作用基于经典的 负反馈思想

$$u(t)=K(y(t)-y_s)$$

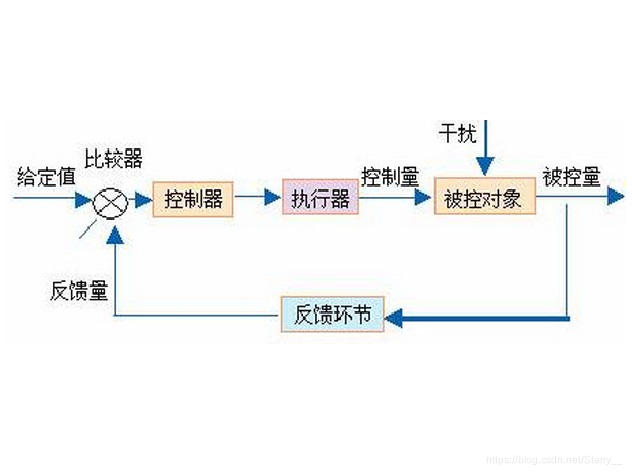
而对于离散系统，在$k$时刻施加的控制信号$u(k)$ 是指在 $k$时刻观测到了系统状态$x(k)$之后施加的控制信号，从而使系统状态由$x(k)$变成$x(k+1)$。而$u(k)$的设计一定是使系统状态与预期值达到一致。

这样控制器和被控对象的交互就构成了一个序列：
$$x(k),u(k),x(k+1),u(k+1),...$$

控制作用就取决于$u(k)$的式子了，经典控制中$u(k)$的表达式是确定的，例如经典PID中的参数是先通过阶跃曲线法调好在加入控制回路中，LQR中的增益K也是提前计算好的。

同时也可以不断实验以调整$u(k)$实现对系统的控制，最终得到针对某个特定系统的控制信号$u(k)$，这就是强化学习的思想。

1.2. 强化学习

强化学习的思路是是使智能体不断地控制，不断地从控制结果调整控制信号$u(k)$，最终完成控制。只不过强化学习的目标不再是使被控量收敛至预定值，而是达到最大的累积奖励。

比如你在写作业，在不知后果的情况下去打游戏，发现最后会被你妈打一顿。下次在写作业的时候，又去打游戏，然后又被打。长此以往你就知道了，跑去打游戏会被妈妈打，于是你选择继续写作业而不是去打游戏。强化学习就是基于这样的奖励机制调整控制策略的。

• 状态 State：即系统状态$x(k)$。

• 动作 Action：针对当前状态施加的控制信号$u(k)$，从而智能体到达一个新的状态$x(k+1)$

• 奖励 Reward：在状态$x(k)$下应用某种动作$u(k)$转移至另一个状态$x(k+1)$，会给出一个奖励值$reward[x(k),u(k)]$

• 值函数 Value function：在状态$x(k)$下应用某种动作$u(k)$会给出一个到达终止状态的累积奖励的期望$valueFunction[x(k),u(k)]$

  值函数和奖励的区别在于，奖励只表达这一步行动的奖励值，值函数表达的是 这一步为开始，最终到达终止状态的所有奖励的和的期望值。即值函数衡量的是这一步对整体的贡献。当然值函数一定包括这一步的奖励。

• 策略 Policy：根据当前状态得出动作的方法，是基于值函数最大得出的动作，即$u(k)=Policy(x(k),valueFunction())$。强化学习关注的是长远的利益而非眼前的奖励。

因此强化学习的目标就是得到 策略Policy，使智能体在任意状态下 达到最大的累积收益。

而这个策略的得出，则需要不断地训练调整得出。就需要智能体不断地探索数据，探索每一步的未来的累积收益如何，并利用这些探索的数据进行策略更新。

参考资料

1. 强化学习(一)：简介

2. 马尔科夫决策过程(Markov decision process, MDP)

马尔科夫决策过程 是强化学习中智能体应用策略的过程，与离散系统的控制类似，在当前状态施加一个行为，得到新的状态，并得到一个收益。
$$x(k),u(k),reward(k+1),x(k+1),u(k+1),...$$

2.1. 定义

典型的MDP包含如下五个要素

其中

• $S$：系统状态的有限集合
• $A$：系统可采取的行动的的有限集合
• $\pi (a|s)$：表示在状态$s$下选择动作$a$的概率，可看作在该状态下的随机策略。$\pi (s)$表示状态$s$下选择的动作，为确定性策略。用$\pi$表示任意状态下的动作策略。
• $R(s,a,s^{\prime })$：收益，表示在状态$s$下采取动作$a$到达新状态$s^{\prime }$而获得的奖励。
• $G$：回报，在时间$[1,T]$内所有行动的收益累积

因此MDP就是在状态$s$下根据$\pi (a|s)$求得行为 a a