强化学习之马尔科夫决策

引言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

---

一、算法介绍

强化学习（Reinforcement Learning, RL） 是一类用于训练智能体（agent）与环境交互并获得最佳决策策略的机器学习方法。在这个过程中，智能体通过行动影响环境，并根据环境反馈（奖励或惩罚）来调整自己的决策。强化学习的目标是找到一个策略，使得在长期内获得的累计奖励最大化。

马尔科夫决策过程（Markov Decision Process, MDP） 是强化学习的数学框架。MDP通过状态、动作、奖励和转移概率描述了智能体与环境的交互过程。

MDP由五元组$(S,A,P,R,\gamma )$定义：

• $S$：状态空间，表示智能体所处的所有可能的状态集合。
• $A$：动作空间，表示智能体在某个状态下可以选择的所有可能的动作。
• $P(s^{\prime }|s,a)$：转移概率函数，表示智能体在状态$s$下执行动作$a$后转移到状态$s^{\prime }$的概率。
• $R(s,a)$：奖励函数，表示智能体在状态$s$执行动作$a$后获得的即时奖励。
• $\gamma$：折扣因子，取值范围为$0\le \gamma \le 1$，用于平衡当前奖励和未来奖励的相对重要性。

强化学习的目标是找到一个策略$\pi (s)$，使得智能体能够最大化其期望累计奖励。累计奖励通常定义为从当前状态开始到未来某个时刻的所有奖励的加权和，表达式为：

$$G_t=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$

其中，$G_t$为从时间步$t$开始的累计回报，$\gamma$为折扣因子，表示未来奖励的重要性。

二、算法原理

MDP的核心问题在于通过策略$\pi (s)$最大化每个状态的期望奖励。为此，可以使用**贝尔曼方程（Bellman Equation）**来递归定义状态值函数$V(s)$和动作值函数$Q(s,a)$：

1. 状态值函数：表示在状态$s$下，按照策略$\pi$执行时的期望累计奖励。状态值函数的贝尔曼方程为：

$$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)\sum _{s^{\prime }\in S}P(s^{\prime }|s,a)[R(s,a)+\gamma V^{\pi }(s^{\prime })]$$

2. 动作值函数：表示在状态$s$下执行动作$a$时的期望累计奖励。动作值函数的贝尔曼方程为：

$$Q^{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })$$

通过上述递归方程，我们可以计算每个状态或状态-动作对的期望值，进而选择使期望值最大的动作来形成最优策略。

策略迭代和值迭代是解决MDP问题的两种主要方法。

• 策略迭代（Policy Iteration）：通过不断估计当前策略的值函数并改进策略来找到最优策略。
• 值迭代（Value Iteration）：直接通过更新状态值函数来找到最优策略。

三、案例分析：多城市天气旅行决策

1. 问题描述

假设有一个旅行者正在两个城市之间来回旅行，这两个城市分别是城市A和城市B。每个城市都有三种天气状态：晴天、小雨、暴雨，并且旅行者需要根据当前的天气状态选择采取某种行动，例如：

• 在当前城市停留。
• 从城市A前往城市B，或者从城市B前往城市A。
• 在当前城市的不同天气条件下采取相应的行动（如带伞、留在室内等）。

旅行者的目标是尽可能获得最高的长期回报，其中每个行动的回报取决于天气、城市和所采取的行动。具体来说，旅行者希望在晴天时享受外出活动（高奖励），而在暴雨时选择避免不必要的旅行（高惩罚）。

2. MDP定义

2.1 状态空间 $S$

• 状态表示当前城市和天气组合，共有6种状态：
  • $S=\{(\text{A, 晴天}),(\text{A, 小雨}),(\text{A, 暴雨}),(\text{B, 晴天}),(\text{B, 小雨}),(\text{B, 暴雨})\}$

2.2 动作空间 $A$

• 旅行者在每种天气状态下的可选行动如下：
  • 在当前城市停留（停留）
  • 从城市A前往城市B，或从城市B前往城市A（旅行）
  • 在当前天气下外出活动（外出）
  • 在当前天气下留在室内（室内）

动作空间为：

• A = { 停留 , 旅行 , 外出 , 室内 } A = \{ \text{停留}, \text{旅行}, \text{外出}, \text{室内} \} A={停留,旅行,外出,室内}

2.3 转移概率 $P(s^{\prime }|s,a)$

• 天气变化和城市之间的转移遵循一定的概率。假设：
  • 在城市A或城市B的晴天，下一时刻有30%的概率转变为小雨，10%的概率转变为暴雨。
  • 小雨有20%的概率转变为暴雨，40%的概率转变为晴天。
  • 暴雨有50%的概率转变为小雨，50%的概率继续暴雨。
  • 在进行城市间旅行时，旅行者到达目标城市后会受到该城市当前天气的影响。

2.4 奖励函数 $R(s,a)$

• 奖励与天气和行动相关：
  • 晴天外出：$R=10$（获得较大乐趣）
  • 小雨外出：$R=5$（享受有限）
  • 暴雨外出：$R=-20$（大惩罚，极度不适）
  • 室内活动：$R=0$（无奖惩）
  • 在暴雨中进行城市旅行：$R=-50$（大惩罚，旅行非常不便）
  • 在小雨中旅行：$R=-10$
  • 在晴天旅行：$R=0$（无奖惩）

2.5 折扣因子 $\gamma$

• 折扣因子$\gamma =0.95$，表示长期奖励较为重要。

3. 代码实现

我们将基于上述MDP模型，使用值迭代算法来求解最优策略。

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimSun']
plt.rcParams['axes.unicode_minus'] = False

# 定义状态、动作、转移概率和奖励函数
states = ['A_晴天', 'A_小雨', 'A_暴雨', 'B_晴天', 'B_小雨', 'B_暴雨']
actions = ['停留', '旅行', '外出', '室内']

# 定义转移概率
transition_probabilities = {
    'A_晴天': {'停留': [0.6, 0.3, 0.1], '旅行': [0.6, 0.3, 0.1], '外出': [0.6, 0.3, 0.1], '室内': [0.6, 0.3, 0.1]},
    'A_小雨': {'停留': [0.4, 0.4, 0.2], '旅行': [0.4, 0.4, 0.2], '外出': [0.4, 0.4, 0.2], '室内': [0.4, 0.4, 0.2]},
    'A_暴雨': {'停留': [0.5, 0.5, 0.0], '旅行': [0.5, 0.5, 0.0], '外出': [0.5, 0.5, 0.0], '室内': [0.5, 0.5, 0.0]},
    'B_晴天': {'停留': [0.6, 0.3, 0.1], '旅行': [0.6, 0.3, 0.1], '外出': [0.6, 0.3, 0.1], '室内': [0.6, 0.3, 0.1]},
    'B_小雨': {'停留': [0.4, 0.4, 0.2], '旅行': [0.4, 0.4, 0.2], '外出': [0.4, 0.4, 0.2], '室内': [0.4, 0.4, 0.2]},
    'B_暴雨': {'停留': [0.5, 0.5, 0.0], '旅行': [0.5, 0.5, 0.0], '外出': [0.5, 0.5, 0.0], '室内': [0.5, 0.5, 0.0]},
}

# 定义奖励函数
rewards = {
    'A_晴天': {'停留': 0, '旅行': 0, '外出': 10, '室内': 0},
    'A_小雨': {'停留': 0, '旅行': -10, '外出': 5, '室内': 0},
    'A_暴雨': {'停留': 0, '旅行': -50, '外出': -20, '室内': 0},
    'B_晴天': {'停留': 0, '旅行': 0, '外出': 10, '室内': 0},
    'B_小雨': {'停留': 0, '旅行': -10, '外出': 5, '室内': 0},
    'B_暴雨': {'停留': 0, '旅行': -50, '外出': -20, '室内': 0},
}

gamma = 0.95  # 折扣因子

# 初始化状态值函数
V = {state: 0 for state in states}

# 值迭代算法
def value_iteration(states, actions, transition_probabilities, rewards, gamma, iterations=1000):
    for _ in range(iterations):
        new_V = V.copy()
        for state in states:
            Q_values = []
            for action in actions:
                Q_value = rewards[state][action] + gamma * sum(
                    [p * V[next_state] for p, next_state in zip(transition_probabilities[state][action], states)]
                )
                Q_values.append(Q_value)
            new_V[state] = max(Q_values)
        V.update(new_V)
    return V

# 运行值迭代
optimal_values = value_iteration(states, actions, transition_probabilities, rewards, gamma)
print("各状态的最优值：", optimal_values)

# 提取最优策略
def extract_policy(states, actions, transition_probabilities, rewards, gamma, V):
    policy = {}
    for state in states:
        Q_values = []
        for action in actions:
            Q_value = rewards[state][action] + gamma * sum(
                [p * V[next_state] for p, next_state in zip(transition_probabilities[state][action], states)]
            )
            Q_values.append(Q_value)
        policy[state] = actions[np.argmax(Q_values)]
    return policy

optimal_policy = extract_policy(states, actions, transition_probabilities, rewards, gamma, optimal_values)
print("最优策略：", optimal_policy)

# 状态值函数可视化
def plot_value_function(optimal_values):
    states = list(optimal_values.keys())
    values = list(optimal_values.values())

    plt.figure(figsize=(8, 5))
    plt.bar(states, values, color='skyblue')
    plt.xlabel('状态 (城市_天气)')
    plt.ylabel('值函数 V(s)')
    plt.title('不同状态下的最优值函数')
    plt.show()

# 调用可视化函数
plot_value_function(optimal_values)

4.结果分析

运行代码后得到如下结果：

各状态的最优值：

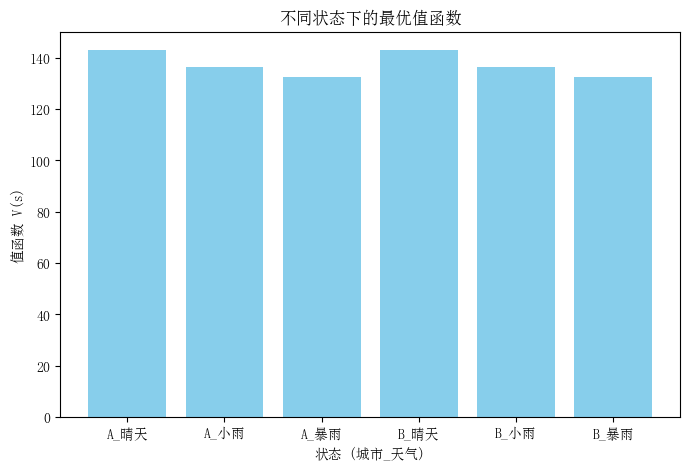
{‘A_晴天’: 142.82961173780058, ‘A_小雨’: 136.2258139116578, ‘A_暴雨’: 132.5513271834927, ‘B_晴天’: 142.82961173780058, ‘B_小雨’: 136.2258139116578, ‘B_暴雨’: 132.5513271834927}

最优策略：

{‘A_晴天’: ‘外出’, ‘A_小雨’: ‘外出’, ‘A_暴雨’: ‘停留’, ‘B_晴天’: ‘外出’, ‘B_小雨’: ‘外出’, ‘B_暴雨’: ‘停留’}

绘制不同状态下的最优值函数柱状图如下：

四、总结

通过这篇文章，我们可以看到，MDP模型在复杂环境中的应用十分广泛，无论是在天气预测、自动驾驶还是机器人控制等领域，MDP都能有效帮助智能体进行合理决策。未来的研究方向可以进一步扩展到更加复杂的实际场景，优化算法，增强系统的计算效率和实际应用能力。