BZOJ1143[CTSC2008] 祭祀river

原题链接：https://www.lydsy.com/JudgeOnline/problem.php?id=1143

祭祀river

Description

在遥远的东方，有一个神秘的民族，自称Y族。他们世代居住在水面上，奉龙王为神。每逢重大庆典， Y族都会在水面上举办盛大的祭祀活动。我们可以把Y族居住地水系看成一个由岔口和河道组成的网络。每条河道连接着两个岔口，并且水在河道内按照一个固定的方向流动。显然，水系中不会有环流（下图描述一个环流的例子）。

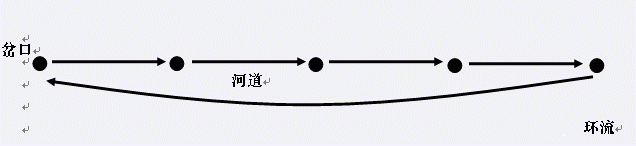
由于人数众多的原因，Y族的祭祀活动会在多个岔口上同时举行。出于对龙王的尊重，这些祭祀地点的选择必须非常慎重。准确地说，Y族人认为，如果水流可以从一个祭祀点流到另外一个祭祀点，那么祭祀就会失去它神圣的意义。族长希望在保持祭祀神圣性的基础上，选择尽可能多的祭祀的地点。

Input

第一行包含两个用空格隔开的整数N、M，分别表示岔口和河道的数目，岔口从1到N编号。

接下来M行，每行包含两个用空格隔开的整数u、v，描述一条连接岔口u和岔口v的河道，水流方向为自u向v。
N≤100M≤1000

Output

第一行包含一个整数K，表示最多能选取的祭祀点的个数。

Sample Input

4 4
1 2
3 4
3 2
4 2

Sample Output

2

HINT

【样例说明】

在样例给出的水系中，不存在一种方法能够选择三个或者三个以上的祭祀点。包含两个祭祀点的测试点的方案有两种：

选择岔口1与岔口3（如样例输出第二行），选择岔口1与岔口4。

水流可以从任意岔口流至岔口2。如果在岔口2建立祭祀点，那么任意其他岔口都不能建立祭祀点。

但是在最优的一种祭祀点的选取方案中我们可以建立两个祭祀点，所以岔口2不能建立祭祀点。对于其他岔口至少存在一个最优方案选择该岔口为祭祀点，所以输出为1011。

题解

这道题求的是最长反链，在$\mathcal{DAG}$中与最小链覆盖等价。

但我们不能直接求出最小链覆盖，所以先用一个$\mathcal{Floyd}$传递闭包将能到达的点直接连在一起，新建的图上的最小路径覆盖等于原图的最小链覆盖。

怎么求最小路径覆盖呢？？？

我们将每个点拆成两份，如果可达则连边，样例建出来的图如下，图中边权都为$1$：

建图可以这么理解：初始每个点位单独的链，每流过一单位流量就相当于把一条链接到另一条链上，链的数目$-1$，所以最终答案为$n-maxflow$。

代码

#include<bits/stdc++.h>
using namespace std;
const int M=10005,inf=0x3f3f3f3f;
struct sd{int to,fl;}ed[M];
bool sq[M][M];
int s,t,n,m,id,d[M];
vector<int>mmp[M];
queue<int>dui;
void add(int f,int t,int w){mmp[f].push_back(id);ed[id++]=(sd){t,w};mmp[t].push_back(id);ed[id++]=(sd){f,0};}
bool bfs()
{
    memset(d,0,sizeof(d));d[s]=1;dui.push(s);int hh,to,fl,f;
    while(!dui.empty())
    {
        f=dui.front();dui.pop();
        for(int i=mmp[f].size()-1;i>=0;--i){hh=mmp[f][i],to=ed[hh].to,fl=ed[hh].fl;if(d[to]||!fl)continue;d[to]=d[f]+1;dui.push(to);}
    }
    return d[t];
}
int dfs(int v,int e,int minn)
{
    if(v==e||!minn)return minn;int ans=0,tmp,hh,fl,to;
    for(int i=mmp[v].size()-1;i>=0;--i)
    {
        hh=mmp[v][i],to=ed[hh].to,fl=ed[hh].fl;
        if(d[to]!=d[v]+1||!fl)continue;
        tmp=dfs(to,e,min(fl,minn-ans));
        if(!tmp)continue;
        ed[hh].fl-=tmp,ed[hh^1].fl+=tmp;ans+=tmp;
    }
    return ans;
}
void in(){int a,b;scanf("%d%d",&n,&m);for(int i=1;i<=m;++i)scanf("%d%d",&a,&b),sq[a][b]=1;}
void ac()
{
    t=(n<<1)+1;int ans=0;
    for(int j=1;j<=n;++j)for(int i=1;i<=n;++i)for(int k=1;k<=n;++k)if(sq[i][j]&&sq[j][k])sq[i][k]=1;
    for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)if(i!=j&&sq[i][j])add(i,j+n,1);
    for(int i=1;i<=n;++i)add(s,i,1),add(i+n,t,1);
    while(bfs())ans+=dfs(s,t,inf);
    printf("%d",n-ans);
}
int main(){in();ac();}