（详解）无指针AC自动机

在经历了一上午的奋斗以后，博主的AC自动机总算过了，其实在有了对KMP算法理解后，是很容易就能理解AC自动机的，Trie树的结构也跟博主的上一篇博客讲的差不多，插入的函数可以说是一模一样的，主要难度在于bfs求构造fail和最后匹配的时候的跳转。
无指针的AC自动机跟带指针的比起来，时间复杂度稍微多了一点（大概两倍。。。），不过一般不会被卡掉,开O2优化还可以比带指针的快一点。值得一提的是，博主的非指针代码消耗的空间只有不加任何优化的指针代码消耗空间的十分之一甚至更少（虽然博主这个蒟蒻并不知道为什么）。再加上无指针代码比较好懂，博主的代码也比较适合初学者参考（毕竟水平相近。。），所以博主对这篇博客的质量还是比较有信心，希望大家能通过我的这篇博客学会/理解AC自动机。

下面进入正题：
　AC自动机详解

例题链接在此：洛谷P3796，本篇博客使用的代码都是基于这道例题的，建议大家先戳进去看一下。
　　前置技能：
　　·KMP单模匹配算法
　　·Trie树（字典树）
　　（还不懂的小伙伴请参照博主前面的博客（虽然水的一匹））
　　简介（粘自百度）：
　　Aho-Corasick automaton，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。
　　要学会AC自动机，我们必须知道什么是Trie，也就是字典树。Trie树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。
　　原理简述：
　　如题，这里仅仅简述一下，更详细的部分需要在后面代码实现板块结合代码讲解，请读者耐心看下去
　　AC自动机运用了KMP的思想，相当于把next数组变成了fail指针，把所有需要匹配的模式串都装进Trie树里。匹配的时候直接将文本串放进去Trie树里跑就行了，复杂度大概为O(n+∑m)即文本串和模式串长度之和，同样是线性的，充满科学性。在失配的时候沿着fail指针跳转，可以利用已有的匹配信息继续匹配，从而大大降低复杂度。
　　代码实现+详细讲解：
　　根据题目的要求，定义结构体如下：

struct node{
	int son[30],cot,x,fail;
	//son表示子节点的编号，0~25表示a~z
	//cot表示该字符的出现次数
	//x表示该节点对应的单词编号，仅在have为真时有效
	//fail就是失配指针
	bool have;//have表示该节点是否存在单词
};

再开如下几个数组：

char txt[1000005],ch[155][75 ;//txt为文本串，ch保存模式串
//不知道为什么把ch数组的最后一个右括号打上后代码块就没有颜色了
//所以这里少打了一个右括号
int ti[155],num,maxn;//ti[i]保存第i个单词的出现次数
//num为编号，maxn为最多的出现次数
node trie[20005];//Trie树

接下来是简单的插入操作，跟Trie树基本一样：

void insert(char ch[],int hh)
{//ch为要插入的字符串，hh为该字符串的编号
	int len=strlen(ch);
	int a=0,b;
	for(int i=0;i<len;++i)
	{//顺着字符串向下构造
		b=ch[i]-'a';
		if(!trie[a].son[b])
		{//如果这个节点还没有出现过，赋一个编号num
			trie[a].son[b]=++num;
		}
		a=trie[a].son[b];//继续向下
	}
	trie[a].have=1;//把终点的have标成true，表示这儿存在单词
	trie[a].x=hh;//指向对应的单词
}

初步构造出的Trie树如图（以存入单词abc，abax，abay，c，bcd，bce为例）：
　　

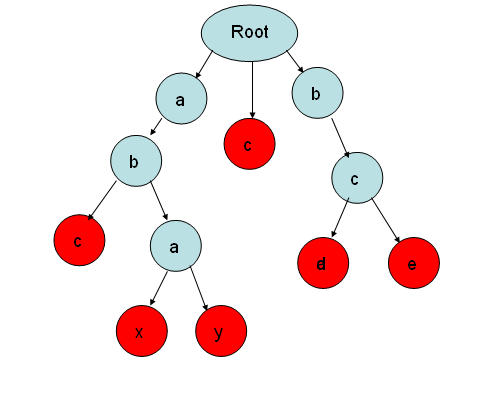
红色的点的have为真，表示这里存在一个单词，这就是一棵纯种的Trie树（详见上一篇博客）。
　　那么接下来就需要添加fail指针了，这也是AC自动机的精髓所在，是减少复杂度的关键，可以通过bfs实现，详解见后：

void getfail()
{
	queue<int>dui;//bfs队列
	dui.push(0);//先把根节点放入队列
	int a;
	while(!dui.empty())
	{
		a=dui.front();
		dui.pop();//bfs基本操作
		for(int i=0;i<26;++i)
		{//遍历所有节点
			if(trie[a].son[i])
			{
				if(a==0)
				{//当节点为第一层节点时，fail肯定指向0啦
					trie[trie[a].son[i]].fail=0;
				}
				else
				{//然后就根据已经求出了的fail指针跳转
					int p=trie[a].fail;
					while(p!=-1)
					{
						if(trie[p].son[i])
						{//如果字符可以匹配
						//那么这个fail就为当前最优解，至于为什么后面有讲解
							trie[trie[a].son[i]].fail=trie[p].son[i];
							break;
						}
						//如果没找到就一直跳转
						p=trie[p].fail;
					}
					if(p==-1)
					{//如果已经跳到根节点了，就让fail指向根节点
						trie[trie[a].son[i]].fail=0;
					}
				}
				dui.push(trie[a].son[i]);
			}
		}
	}
}

在调用getfail函数以后，Trie会变成下图这样（图中紫色的箭头为新构造的fail指针的指向），博主将结合此图进行讲解，也请读者在阅读时参考代码，对照原理与代码：
　　
　　
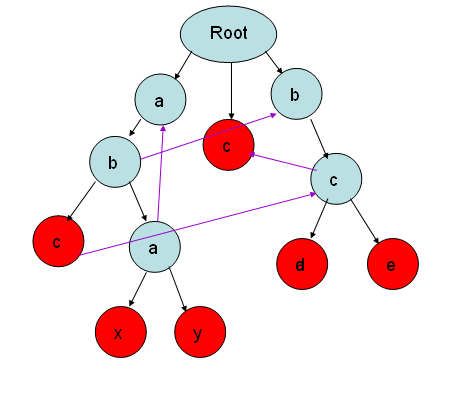
　　·fail指针指向的到底是什么呢？
　　fail指针指向的是跟当前节点所代表的字符串的后缀相同的最长的字符串的末尾编号（反复阅读，反复阅读！）
　　相信大家多半是一脸懵逼的，别急，博主的详解马上到。举个例子来讲，正如图中所示，字符串abc的c指向了bc的b，我们按照上面的那句话一一对照如下：
　　fail指针指向的是跟当前节点（c）所代表的字符串（abc）的后缀（bc）相同的最长的字符串（bc）的末尾（c）编号。
　　
　　·fail指针有什么作用？
　　通过fail指针，我们可以在匹配一个串时，“顺便”将另外一个跟自己的后缀相同的字符串匹配了，失配时也可以直接沿着fail指针进行跳转。
　　
　　·fail指针如何实现这个作用？
　　在匹配时，如果串abc都能被匹配，那么作为abc子串的bc自然就可以匹配，字符串c也同理。在失配时，也可以通过fail指针跳到另一个串利用上一次匹配的成果继续匹配，比如下面这个情况：
　　
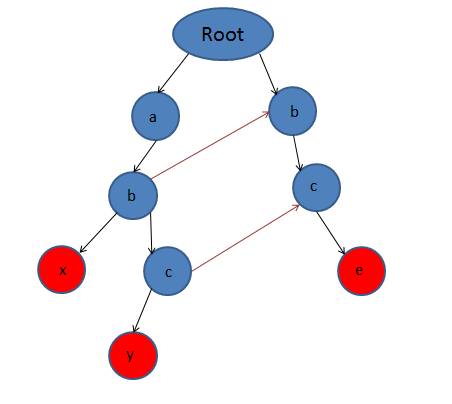
　　当匹配字符串时，当匹配到左边的节点c时，下一个字符是e，那么便无法匹配y，于是通过fail指针跳转到右边的c节点，于是就匹配到了字符串bce。
　　
　　·怎么求出fail指针？
　　我们的主要思路就是利用已经求出来的fail指针进行递推，初始情况就是第一层的节点全部指向根节点。因为前面的fail指针已经匹配成功，那么如果下一个字符相同，则又可以在下一个字符间建立fail指针，此时的fail指针指针就是当前的最优解了（参考上图中的b->b，c->c）。
　　
　　针对getfail函数的讲解总算是告一段落了，那么有了对于fail指针的深刻理解理解，再结合kmp算法，匹配函数就好理解多了，让我们来看看代码：

void cmp(char ch[])
{//传的参数是文本串
	int len=strlen(ch);
	int a=0,b;
	for(int i=0;i<len;++i)
	{
		b=ch[i]-'a';
		while(a!=0&&!trie[a].son[b])
		{//如果失配了，就沿着fail指针跳转直到可以匹配
			a=trie[a].fail;
		}
		if(trie[a].son[b])
		{//匹配成功后就继续向下
			a=trie[a].son[b];
		}
		int p=a;
		while(p!=0)
		{//“顺便”将fail指针指向的字符串一起匹配了
			if(trie[p].have)
			{//如果这里存在单词，进行统计
				++ti[trie[p].x];//出现次数计数
				maxn=max(ti[trie[p].x],maxn);//求最大出现次数
				//（可以放在最后做，应该快一点，博主懒得改）
			}
			p=trie[p].fail;//跳呀跳。。。
		}
	}
}

针对模板题的温馨提示：
　　模板例题中，输出的字符串是要按输入的顺序的（没有看题的人可能不知道我在说什么），所以最后排序找出现次数最多的几个串的时候会打乱顺序，莫名WA。。。除了博主的解决思路（较快），还可以再写一个查找函数或再跑一遍（两者时间复杂度差不多但相当于是重复操作了，复杂度乘2，所以博主自以为自己的方法还是很不错的）。由于是算法讲解，所以针对例题不多讲，反正是板子题，大家还可以自己看题解。
　　例题AC代码如下：

#include<bits/stdc++.h>
using namespace std;
const int M=1e6+5,N=155;
char ch[N][N],txt[M];
int t[N],mx,n,tot,son[N*N][27],id[N*N],fail[N*N];
bool is[N*N];
queue<int>dui;
void insert(int num,int len)
{
	int v=0,s;
	for(int i=1;i<=len;++i)
	{
		s=ch[num][i]-'a';
		if(!son[v][s])son[v][s]=++tot;
		v=son[v][s];
	}
	is[v]=1;id[v]=num;
}
void bfs()
{
	int v,p;dui.push(0);
	while(!dui.empty())
	{
		v=dui.front();dui.pop();
		for(int i=0;i<26;++i)
		{
			if(!son[v][i])continue;
			if(!v)fail[son[v][i]]=0;
			else{for(p=fail[v];~p;p=fail[p])if(son[p][i]){fail[son[v][i]]=son[p][i];break;}if(p==-1)fail[son[v][i]]=0;}
			dui.push(son[v][i]);
		}
	}
}
void cmp()
{
	int len=strlen(txt+1),v=0,s,p;
	for(int i=1;i<=len;++i)
	{
		s=txt[i]-'a';
		while(v&&!son[v][s])v=fail[v];
		if(son[v][s])v=son[v][s];
		for(p=v;p;p=fail[p])if(is[p])++t[id[p]],mx=max(mx,t[id[p]]);
	}
}
void reset(){tot=mx=0;memset(t,0,sizeof(t));memset(son,0,sizeof(son));memset(is,0,sizeof(is));memset(id,0,sizeof(id));memset(fail,0,sizeof(fail));fail[0]=-1;}
void in(){for(int i=1;i<=n;++i)scanf("%s",ch[i]+1),insert(i,strlen(ch[i]+1));scanf("%s",txt+1);}
void ac()
{
	bfs();cmp();printf("%d\n",mx);
	for(int i=1;i<=n;++i)if(t[i]==mx)printf("%s\n",ch[i]+1);
}
int main(){while(scanf("%d",&n)&&n)reset(),in(),ac();}

感谢各位老爷能够坚持看到这里，之前一直说的粗长AC自动机详解总算是写完了。其实博主也是一边打博客一边对代码加深理解，希望各位可以多打几遍代码来加深理解。AC自动机确实是一个非常巧妙的算法，能够想出这样的算法确实是天犇了，不过算法已经被构想出来了，结合KMP与Trie树的相关知识，理解还是不难的。希望本篇博客能帮到大家。