本文探讨了DDPM（深度变分自编码器中的扩散模型）的反向扩散过程中的局限性，提出DDIM方法，通过跳过马尔可夫步骤来加速推理。DDIM利用高斯噪声和U-Net的不变性，即使在不改变正向扩散过程的情况下，也能提供高效且生成质量稳定的反向扩散。
DDPM的重大缺陷在于其在反向扩散的过程中需要逐步从xtx_txt倒推到x0x_0x0，因此其推理速度非常缓慢。相反，DDPM的训练过程是很快的，可以直接根据x0x_0x0到xtx_txt添加的高斯噪声ϵ\epsilonϵ完成一次训练。
为了解决这个问题，就有了DDIM，且包括Stable Diffusion在内的现今广泛使用的Diffusion模型都在使用DDIM。
在DDPM中，我们利用P(xt−1∣xt)P(x_{t-1}|x_{t})P(xt−1∣xt)来逐步倒推至最开始的x0x_0x0，这一过程是遵守马尔可夫过程的，即每个时刻的状态只跟上一个时刻的状态有关，因此只能一步步的倒退回去。而实际上，我们最初就是简化了加噪过程，从x0x_0x0到xtx_txt直接一步到位，并没有使用P(xt∣xt−1)P(x_t|x_{t-1})P(xt∣xt−1)这样按部就班的马尔可夫过程。那么，能不能在倒推的时候也采用类似的思路进行“跳步”，从而达到加快推理的目的呢？
假设我们现在想直接从kkk时刻跳到sss时刻，且有s<k−1s<k-1s<k−1，那么仿照DDPM我们可以写出下列式子
P(xs∣xk,x0)=P(xk∣xs,x0)P(xs∣x0)P(xk∣x0)
P(x_s|x_k,x_0)=\frac{P(x_k|x_s,x_0)P(x_s|x_0)}{P(x_k|x_0)}
P(xs∣xk,x0)=P(xk∣x0)P(xk∣xs,x0)P(xs∣x0)
其中P(xs∣x0)P(x_s|x_0)P(xs∣x0)和P(xk∣x0)P(x_k|x_0)P(xk∣x0)满足的分布都好说，可以从正向扩散公式中得出。不知道怎么表示的这一项P(xk∣xs,x0)P(x_k|x_s,x_0)P(xk∣xs,x0)因为反正整个模型都没有用过，所以可以先不考虑。（这个解释确实很神奇，但是他有用啊）其实就是说DDIM打破了马尔可夫链从000开始逐个往前扩散的模型，而是直接采用从x0x_0x0到xtx_txt的直接公式作为整个模型的backbone，因此从sss到kkk的正向过程可以“按需定义”，而不必采用DDPM里的公式，所以在这里就直接被忽略了。
言归正传，我们尝试求解一下上面的式子。参考DDPM，我们也可以假设P(xs∣xk,x0)P(x_s|x_k,x_0)P(xs∣xk,x0)是满足正态分布的，其均值为xkx_kxk和x0x_0x0的加权和，记为
P(xs∣xk,x0)∼N(nx0+mxk,σ2)
P(x_s|x_k,x_0)\sim\mathcal{N}(nx_0+mx_k, \sigma^2)
P(xs∣xk,x0)∼N(nx0+mxk,σ2)写出xsx_sxs的表达式
xs=(nx0+mxk)+σϵ,ϵ∈N(0,1)
x_s=(nx_0+mx_k)+\sigma\epsilon,\epsilon\in\mathcal{N}(0,1)
xs=(nx0+mxk)+σϵ,ϵ∈N(0,1)将xk=α‾kx0+1−a‾kϵ′x_k=\sqrt{\overline{\alpha}_k}x_0+\sqrt{1-\overline{a}_k}\epsilon'xk=αkx0+1−akϵ′代入，可得
xs=(nx0+mxk)+σϵ=(n+ma‾k)x0+(m1−a‾kϵ′+σϵ)=(n+ma‾k)x0+m2(1−a‾k)+σ2ϵ′′
\begin{aligned}
x_s&=(nx_0+mx_k)+\sigma\epsilon\\
&=(n+m\sqrt{\overline{a}_k})x_0+(m\sqrt{1-\overline{a}_k}\epsilon'+\sigma\epsilon)\\
&=(n+m\sqrt{\overline{a}_k})x_0+\sqrt{m^2(1-\overline{a}_k)+\sigma^2}\epsilon''
\end{aligned}
xs=(nx0+mxk)+σϵ=(n+mak)x0+(m1−akϵ′+σϵ)=(n+mak)x0+m2(1−ak)+σ2ϵ′′注意到这个的形式与从x0x_0x0直接到xsx_sxs的公式很像，即xs=α‾sx0+1−a‾sϵx_s=\sqrt{\overline{\alpha}_s}x_0+\sqrt{1-\overline{a}_s}\epsilonxs=αsx0+1−asϵ，所以我们可以将这两个系数对应起来求解，得
m=1−α‾s−σ21−α‾k,n=α‾s−1−α‾s−σ21−α‾kα‾k
m=\frac{\sqrt{1-\overline{\alpha}_s-\sigma^2}}{\sqrt{1-\overline{\alpha}_k}},n=\sqrt{\overline{\alpha}_s}-\frac{\sqrt{1-\overline{\alpha}_s-\sigma^2}}{\sqrt{1-\overline{\alpha}_k}}\sqrt{\overline{\alpha}_k}
m=1−αk1−αs−σ2,n=αs−1−αk1−αs−σ2αk将上面的结果带入xsx_sxs的均值nx0+mxknx_0+mx_knx0+mxk，可得
μ=α‾sx0+1−α‾s−σ21−α‾k(xk−α‾kx0)
\begin{aligned}
\mu=\sqrt{\overline{\alpha}_s}x_0+\frac{\sqrt{1-\overline{\alpha}_s-\sigma^2}}{\sqrt{1-\overline{\alpha}_k}}(x_k-\sqrt{\overline{\alpha}_k}x_0)
\end{aligned}
μ=αsx0+1−αk1−αs−σ2(xk−αkx0)这样我们就求得了P(xs∣xk,x0)P(x_s|x_k,x_0)P(xs∣xk,x0)满足的正态分布N(μ,σ2)\mathcal{N}(\mu,\sigma^2)N(μ,σ2)，其中只剩σ\sigmaσ为变量，x0x_0x0可以像DDPM一样反解为 xkx_kxk的表达式代入，通过预测加噪的噪声来得到一个确定的μ\muμ。
至于方差σ\sigmaσ，一般有两种取值，取000时方差为000，这个反向扩散就成了一个确定过程，对应标题中所说的“多样性换运行效率”，此时σ=0\sigma=0σ=0的状态就是我们通常所说的DDIM。而σ=1−at1−a‾t−11−a‾t\sigma=\frac{\sqrt{1-a_t}\sqrt{1-\overline{a}_{t-1}}}{\sqrt{1-\overline{a}_t}}σ=1−at1−at1−at−1，即在DDPM中推出来的方差时，整个过程会退化为DDPM的倒推过程。
需要注意的是，这里的σ\sigmaσ可以自由取值是因为我们假设P(xs∣xk,x0)P(x_s|x_k,x_0)P(xs∣xk,x0)是一个均值μ\muμ未知，方差为σ2\sigma^2σ2的高斯分布，通过求解μ\muμ得到了一个只有σ\sigmaσ为自由变量的xsx_sxs的表达式。可以把σ\sigmaσ视作一个超参数，只是通过实验发现在σ=0\sigma=0σ=0时效果最好。而DDPM中的方差是通过三个已知的正态分布计算来的，本身就是靠计算得来的确定的方差，所以不能随便更改，如果在DDPM的过程中使σ=0\sigma=0σ=0，效果会非常差。
而从实验结果来看，σ=0\sigma=0σ=0的时候还是效果最好的，FID最低。在SSS取505050或100100100，即加速10−2010-2010−20倍时保持相近的生成质量。
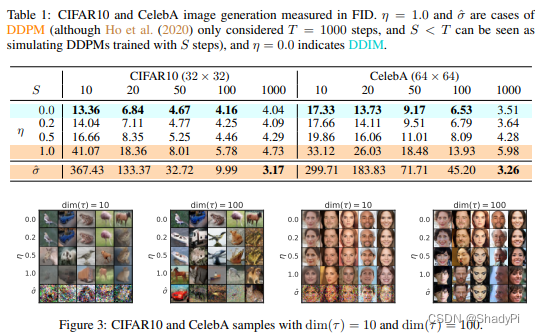
更妙的是，因为DDPM中的U-Net预测的是加在xtx_txt上的噪声ϵ\epsilonϵ，这个是基于正向扩散的公式来的。而DDIM并没有改变这一过程，因此一个训练好的DDPM中的U-Net也可以直接拿到DDIM里面，甚至不需要额外训练。DDIM只是更改了DDPM反向扩散的过程，通过跳步加速推理。
扫一扫
5100
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
