【详解】树状数组

目录：
一、问题引入
二、树状数组
1.实现原理
2.lowbit(x)求解
三、树状数组的应用
1.单点修改
2.区间求和
3.建立树状数组
四、树状数组的扩展
1.求解逆序对
2.二维树状数组
3.初始化
4.树状数组求区间最大/小值
5.区间修改+单点查询+区间查询

一、问题引入

【问题描述】
给定$n$个数$a[1],a[2],a[3],...,a[n]$，现在有下面两种操作：
$（1）$询问区间 $[x,y]$ 的和，并输出。
$（2）$将下标为$x$的数增加$val$。
一共进行$m$次操作。
$1\le n，m\le 100000$，保证每个数在 $int$ 范围内。

方法一：暴力枚举
定义数组$a$存储$n$个数。求区间和的时间复杂度为$O(n)$，将$a[x]$增加$val$的时间复杂度为$O(1)$，总时间复杂度为$O(nm)$。
方法二：前缀和
定义数组$sum$，表示前缀和。求区间和的时间复杂度为$O(n)$，将$a[x]$增加$val$的时间复杂度为$O(n)$，因为每进行增加操作，就需要更新所有前缀和，总时间复杂度为$O(nm)$。

为什么两种方法的时间复杂度都这么高呢？
第一种方法，数组$a$的元素存储的信息只包含一个数，管的太少，所以求和慢。
第二种方法，数组$sum$的元素存储的信息包含了前面的所有数，管的太多，导致修改数值时牵扯到的元素很多，所以修改慢。
因此，那么我们就找一个数组存储的信息包含的数不多，也不少就可以了，这就是——树状数组。

不太多，也不太少这种思想，其实刚好是树状数组的神奇之处。这也是程序设计中的一种思路，取折中后最后的，因此会有这种复杂度$O(logN)，O(\sqrt{N})$，都是在几个操作的极限情况下，找最佳平衡方案。

二、树状数组

1. 实现原理

树状数组是使用二进制来决定包含元素数量的，添加一个数组$c$。
$c[x]$——存储区间结尾为$a[x]$，区间长度为$lowbit(x)$的和，即表示区间$a[x-lowbit(x)+1]$ ~ $a[x]$的和。
$lowbit(x)$——表示$x$二进制最低为$1$的值。
如：$x=110_{(2)}=6_{(10)}，lowbit(x)=10_{(2)}=2_{(10)}$，
再如 ：$x=1000_{(2)}=8_{(10)}，lowbit(x)=10_{(2)}=2_{(10)}$）
例子：如果数组$a$包含$8$个元素，树状数组的形态如下，$c[x]$表示的区间和，$x$的二进制，$lowbit(x)$如下表：

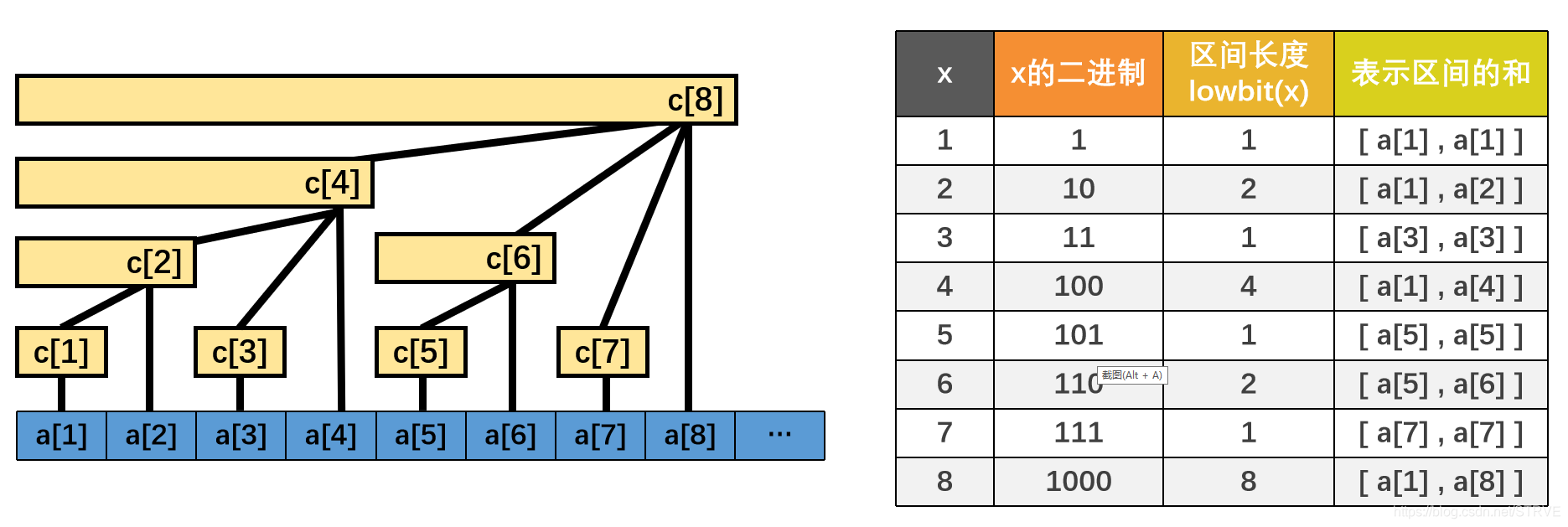
$c$数组最后的形态就像树一样，这就是树状数组名称的由来。
通过这幅图与这张表，可以得出下面的结论：

1. 每个内部结点$c[x]$保存以它为根的子树中所有叶结点的和。
   如：$c[6]，lowbit(6)=2$，保存长度为$2$，结尾为$a[6]$的区间和，$c[6]=a[5]+a[6]$。
   $c[8]，lowbit(8)=8$，保存长度为$8$，结尾为$a[8]$的区间和，$c[6]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]$。
2. 每个内部结点$c[x]$的子结点个数等于$lowbit(x)$的大小。
3. 除树根外，每个内部结点$c[x]$的父亲为$c[x+lowbit(x)]$。
   如$c[3]$与$c[4]$，$3_{(10)}+lowbit(3)=11_{(2)}+1_{(2)}=100_{(2)}=4_{(10)}$，其他结点也类似，有了这个关系，单点修改就容易多了。
4. 树的深度为$O(logN)$，$N$为处理的元素个数。

2. lowbit(x)求解方法

使用位运算，设$x$的第$k$位为$1$，第$0$ ~ $k-1$位都是$0$。
$（1）$先把$x$取反，此时第$k$为变为$0$,第$0$ ~ $k-1$位都为$1$。
$（2）$再令$x=x+1$，此时因为进位，第$k$位变为$1$，第$0$ ~ $k-1$位都为$0$。同时，因为取反操作，第$k+1$位到最高位都与原来相反。
$（3）$再进行与运算，此时，除了第$k$位为$1$，其余全为$0$。
表示为：

lowbit(x)=x&(~x+1)

又因为，在计算机中通常使用补码进行储存，负数的补码是其对应正数二进制所有位取反后加1。因此：~$x=-x+1$。

lowbit(x)=x&(~x+1)=x&(-x)

计算过程大家可以举一个例子在草稿纸上模拟一边。
实现程序：

int lowbit(x)
{
	return x&(-x);		//也可以写成return x&(~x+1);
}

注意：
树状数组能够处理的下标为$1$~$n$，不能出现下标为$0$的情况，$lowbit(0)=0$会陷入死循环。因此，如果出现下标为$0$的情况，可以全部右移一个单位。

三、树状数组应用

1. 单点修改

如果对$a[x]$增加 $val$，那么包含 $a[x]$ 的 $c$ 数组都会改变，通过上图可以知道，即$c[x]$和$c[x]$的祖先结点都增加$val$，可以通过$x+lowbit(x)$求解$x$的父结点。
【程序实现】：

void update(int x,int val)	//a[x]增加val 
{
    for(int i=x;i<=n;i+=lowbit(i))	//i的父结点为i+lowbit(i)
        c[i]+=val;
}

时间复杂度为：O(logN)。

2. 求修改后的区间和

求解区间 $[x,y]$ 的和。
我们发现$c$数组只包含了部分元素，现在我们先求解区间 $[1,x]$ 的和，即前缀和。
对于任意正整数可以写成关于2的不重复次幂相加的形式。
若正整数$x=21$,二进制表示为$10101$，$x=2^4+2^2+2^0$。
对于区间$[1,x]$，根据二进制表示，可以分解成$log(x)$个小区间：
(1)长度为$2^4$的小区间：$[1,2^4]$。
(2)长度为$2^2$的小区间：$[2^4+1,2^4+2^2]$。
(3)长度为$2^0$的小区间：$[2^4+2^2+1,2^4+2^2+2^0]$。
分解出的小区间有个共同特点：
若区间结尾为y，则区间长度就等于lowbit(y)。
所以前缀和$sum[21]=c[2^4+2^2+2^0]+c[2^4+2^2]+c[2^4]$
$c$数组下标y有什么变化呢，每次减少$lowbit(y)$，即求解出二进制每个$1$表示的大小，对应$c$数组。
【程序实现】：

int sum(int x)		//求前缀和a[1]~a[x] 
{	
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        ans+=c[i];
    return ans;
}

知道前缀和，自然就求解出区间$[x,y]$的和$sum(y)-sum(x-1)$。
时间复杂度为：$O(logN)$。

3. 建立树状数组

初始时，将$a$数组的所有元素全部看作为$0$，每输入一个数$a[i]$，可以看作下标为$i$的数增加$a[i]$。
建立树状数组，实际就是$n$次单点更新操作，a数组实际也可以不需要定义。
【程序实现】：

for(int i=1;i<=n;i++)
{
	cin>>a;
	update(i,a);
}

时间复杂度为：$O(NlogN)$。

四、树状数组扩展

1.求逆序对

树状数组也可以用来求解逆序对问题。
对于给定$n$个数$a[1]，a[2]，a[3]......a[n]$，求出有多少对逆序对？
【解决方法】
（1）定义数组$s$，$s[x]$表示数值为$x$出现的次数，即桶计数。
再定义树状数组$c$，$c[x]$表示数值在区间$[x-lobit(x)+1,x]$的个数。
（2）逆序访问$n$个数（$a[n],a[n-1],...a[1]$）,对于$a[i]$，统计前缀和$sum(i-1)$，表示值范围在$1$ ~ $i-1$的个数，因为逆序访问，前缀和包含的数全部比$a[i]$小，且在$a[i]$后面，形成了逆序对$sum[i-1]$个。
（3）将每次前缀和相加，就是最后的答案。
（4）访问完a[i]，就执行单点增加，数值为a[i]的个数+1，即s[a[i]]+1。
如果数值太大，桶装不下怎么办呢？可以使用离散化，所谓离散化就是把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。
例如：我需要求解序列：99999999 199999999 88888888的逆序对，实际可以看作是求序列：1 3 2的逆序对，因为逆序对跟大小关系有关，和具体的值无关。
【程序实现】：
这里的s数组相当于树状数组中的a数组，可以不使用，方便大家理解。

#include<bits/stdc++.h>
#define N 500100
using namespace std;
int n,c[N],a[N],maxn;
int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int val)
{
    for(int i=x;i<=maxn;i+=lowbit(i))	
        c[i]+=val;
}
int sum(int x)
{
    int ans=0;
   for(int i=x;i>0;i-=lowbit(i))
        ans+=c[i];
    return ans;
}
int main()
{
    scanf("%d",&n);
    long long ans=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        maxn=max(maxn,a[i]);	//最大值 
    }
    for(int i=n;i>=1;i--)
    {
        ans+=(long long)sum(a[i]-1);
        update(a[i],1);
    }
    cout<<ans<<endl;
    return 0;
 } 

2.二维树状数组

树状数组也能够在二维数组上也可以应用。
在一维树状数组中， $c[x$]代表的是记录区间尾为x ，长度为$lowbit(x)$的区间和。
所以在二维树状数组当中，定义$c[x][y]$记录的是右下角为$(x,y)$ ，长为$lowbit(x)$,宽为 $lowbit(y)$的区间和。
所以单点修改和区间查询的操作就改成了二维的了。

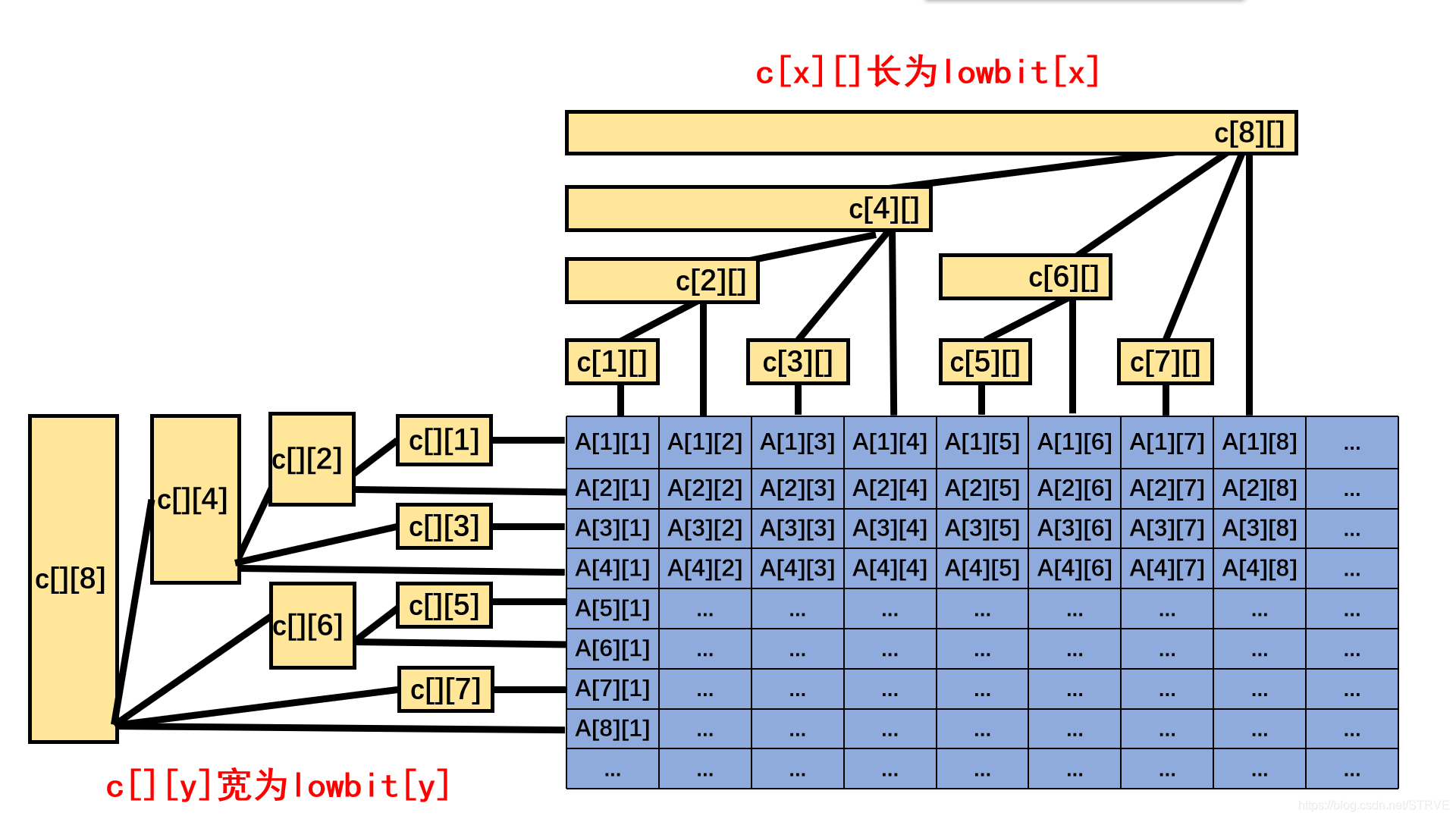
【程序实现】
n行m列的序列

void  update(int x,int y,int val)	//a(x,y)增加val
{
	for(int i=x;i<=n;i+=lowbit(i))	
		for(int j=y;j<=m;j+=lowbit(j))
	     		c[i][j]+=val;
}

int  sum(int x,int y)	//求右下角为(x,y)，长为lowbit(x)，宽为lowbit(y)
{
	int ans=0;
	for(int i=x;i<=n;i+=lowbit(i))	
		for(int j=y;j<=m;j+=lowbit(j))
	     		ans+=c[t][j];
	
	return ans;
}

3.初始化

初始时，可以默认a数组为0，每输入$a[i]$，相当于执行$update(i,a[i])$，实际复杂度为$O(NlogN)$。
我们知道，$c[x]$表示区间结尾为$a[x]$，长度为$lowbit(x)$的区间和，那么可以使用前缀和预处理的方法:
$c[x]=summ[x]-summ[x-lowbit(x)]$
时间复杂度为O(N)。

4.树状数组求前缀最大/小值

使用c[x]维护区间结尾为$a[x]$，长度为$lowbit(x)$的最大值。

void update(int x,int val)	 	//将a[x]更新为val，更新c数组最大值
{
    for(int i=x;i<=n;i+=lowbit(i))	//i的父结点为i+lowbit(i)
        c[i]=max(c[i],val)
}

int sum(int x)			//a[1]~a[x]的最大值
{	
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        ans=max(ans,c[i]);
    return ans;
}

5.区间修改+单点查询+区间查询

区间修改
如果要对某一个区间整体修改怎么办呢？
如果一个一个单点修改，时间复杂度比较高。
这里可以是使用差分数组，将区间修改变为两次单点修改。
如果存在序列$a$的差分数组$s$，对区间$[x,y]$增加$val$，可以视为差分数组：$s[x]+=val，s[y+1]-=val$。
单点查询
求修改后的$a[x]$的值。（差分数组）
实际上就是差分数组的前缀和。
区间查询
知道每个元素a[x]的值，求区间的和，再次使用前缀和即可。（差分数组）