【题解】求后序遍历（二叉树遍历，递归）

题面

【题目描述】
给出二叉树的先序遍历和中序遍历，求后序遍历。
【输入】
输入共两行，第一行一个字符串，表示树的先序遍历，第二行一个字符串，表示树的中序遍历。树的结点一律用小写字母表示。字符串长度小于$100$。
【输出】
输出仅一行，表示树的后序遍历序列。
【样例输入】

abdec
dbeac

【样例输出】

debca

算法分析

二叉树有三种遍历方法：
先序遍历：（1）访问根节点；（2）先序遍历左子树；（3）先序遍历右子树。
中序遍历：（1）中序遍历左子树；（2）访问根节点；（3）中序遍历右子树。
后序遍历：（1）后序遍历左子树；（2）后序遍历右子树；（3）访问根节点。

已知先序遍历和中序遍历：

对于先序遍历，第一个结点为根节点$a$。接下来找出中序遍历的根结点，根据中序遍历的顺序，可以知道，根节点$a$左边为$a$的左子树，右边为$a$的右子树：

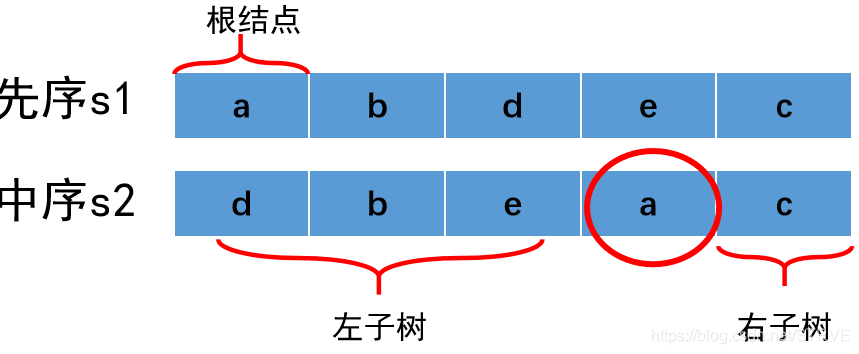
对于先序遍历，根节点$a$后紧跟的为$a$的左子树，左子树访问完之后为$a$的右子树。可以知道，$a$的左子树的结点数目是固定的，那么可以通过中序遍历根节点$a$左边的结点数目，即左子树的结点总数，从而在先序遍历中找到左子树的区间，对于样例，先序遍历中，根节点$a$后$3$个结点为$a$的左子树，剩下的为右子树。
因此左子树的先序遍历为：$bde$，左子树的中序遍历为：$dbe$；
右子树的先序遍历为：$c$，左子树的中序遍历为：$c$；
根结点为$a$。
按照同样的方法，继续对左右子树进行拆分。
假设先序遍历的下标区间为$l_1$~r1r_1