【NOIP2016提高A组五校联考1】道路规划

最新推荐文章于 2022-03-15 22:55:48 发布

SSLGZ_yyc

最新推荐文章于 2022-03-15 22:55:48 发布

阅读量93

点赞数

CC 4.0 BY-SA版权

分类专栏：动态规划 c++ jzoj比赛

本文链接：https://blog.youkuaiyun.com/SSLGZ_yyc/article/details/94565882

c++ 同时被 3 个专栏收录

372 篇文章

订阅专栏

jzoj比赛

206 篇文章

订阅专栏

动态规划

119 篇文章

订阅专栏

本文探讨了如何通过最长下降子序列算法解决特定几何问题，即判断多条线段是否互不相交。通过分析线段相交条件，将问题转化为求解最长下降子序列，给出详细的算法实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

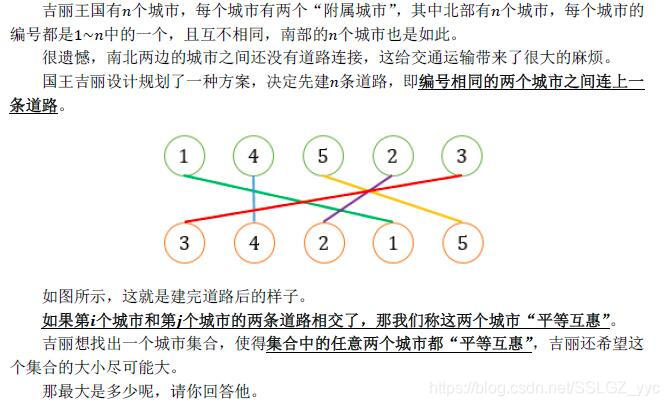
Description

在这里插入图片描述
Input

Output
在这里插入图片描述

Sample Input
5
1 4 5 2 3
3 4 2 1 5

Sample Output
3

Data Constraint
在这里插入图片描述

Hint
在这里插入图片描述

.
.
.
.
.
.
.
分析
我们考虑在什么情况下，
两对点的连线相交。
就是南北两边它们的顺序相反。

再考虑如果两条线段已经相交，
第三条线段在什么情况下是都与它们相交。
就是这条线段的两个端点都跨过了原来的两条线段。

进一步就可以发现这道题目就是求最长下降子序列。

.
.
.
.
.
程序：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

int n,a[100010],b[100010],f[100010],ans=0;

void lds() 
{
    memset(f,127,sizeof(f));
    for (int i=1;i<=n;i++)
		if (a[i]<f[ans])
        {
            ans++;
            f[ans]=a[i];
        } else
        {
    		int l=1,r=ans;
            while (l<r)
            {
                int mid=(l+r)/2;
                if (f[mid]<=a[i]) r=mid; else l=mid+1;
            }
            f[l]=a[i];
        }
}

int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	for (int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x); 
		b[x]=i;
	}
	for (int i=1;i<=n;i++)
		a[i]=b[a[i]];
	lds();
	printf("%d",ans);
	return 0;
}