最小比例(ratio)

Description
图中共有N个点的完全图，每条边都有_权值，每个点也有_权值。要求选出M个点和M-1条边，构成一棵树，使得：

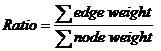
即所有边的权值与所有点的_权值之和的比率最小。

给定N和M，以及N个点的_权值，和所有的边权，要求M个点的最小比率生成树。

Input
第一行包含两个整数N和M(2<=N<=15，2<=M<=N)，表示点数和生成树的点数。

接下来一行N个整数，表示N个点的边_权。

最后N行，每行N列，表示完全图中的边_权。所有点权和边权都在[1,100]之间。

Output
输出最小比率生成树的M个点。当答案出现多种时，要求输出的第一个点的编号尽量小，第一个相同，则第二个点的编号尽量小，依次类推，中间用空格分开。编号从1开始。

Sample Input
输入1：

3 2

30 20 10

0 6 2

6 0 3

2 3 0

输入2：

2 2

1 1

0 2

2 0

Sample Output
输出1：

1 3

输出2：

1 2

Data Constraint
对于30%数据，N<=5。

.
.
.
.
.
.
分析
这是一个相对简单的题。由于n很小，所以直接深搜出m个点的取法，对于每一种取法构成的子图，求其最小生成树，记录边权和比点权和最小的那棵树即可。

.
.
.
.
.
.
程序：