【NOIP2016提高A组五校联考1】排队

最新推荐文章于 2020-08-11 16:12:46 发布

原创最新推荐文章于 2020-08-11 16:12:46 发布 · 151 阅读

0 ·

CC 4.0 BY-SA版权

c++ 同时被 3 个专栏收录

372 篇文章

订阅专栏

jzoj比赛

206 篇文章

订阅专栏

树

31 篇文章

订阅专栏

本文探讨了优先级堆和倍增算法在处理特定数据结构问题中的应用，通过实例详细解析了如何利用这两种算法优化操作效率，实现快速查找和更新。

Description
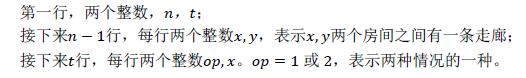
在这里插入图片描述

Input
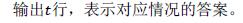
在这里插入图片描述

Output
在这里插入图片描述

Sample Input
5 4
1 2
1 3
3 4
3 5
1 4
2 4
1 2
2 5

Sample Output
3
1
1
2

Data Constraint

在这里插入图片描述

Hint
在这里插入图片描述

.
.
.
.
.
.
分析
首先每个点的优先级是固定的。即，每次新来一个人必定去优先级最高的没人的点
所以我们预处理出每一个点的优先级，就是下一个走进来的人会走到当前优先级最小的那个点，那么我们可以用一个堆来维护，每一次进一个人就出一次堆
对于操作2，我们可以用倍增来找到当前位置上面的一个最接近根节点的一个有人的节点，那么就等于这个节点的人直接走到删除的那个节点那里去了
注意在操作2完了之后要维护一下堆
那么两个操作都是log级别的

.
.
.
.
.
程序：

#include<iostream> 
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;

int dfsx[100010],p[100010],b[100010],dui[400010];
vector<int> a[100010];
int deep[100010],f[100010][20],tot=0,cnt=0;
bool bz[100010];

bool cmp(int x,int y) 
{
	return dfsx[x]<dfsx[y];
}

int js(int x)
{
	int t=0;
	while (x!=0)
	{
		t++;
		x/=2;
	}
	return t-1;
}

void dfs(int x,int father)
{
	f[x][0]=father;
	deep[x]=deep[father]+1;
	for (int i=0;i<=a[x].size()-1;i++)
		if (a[x][i]!=father) dfs(a[x][i],x); 
	dfsx[x]=++cnt;
}

void insert(int x)
{
	tot++;
	dui[tot]=x;
	for (int i=tot;i>=2;i/=2)
		if (p[dui[i]]<p[dui[i/2]]) swap(dui[i],dui[i/2]); else break;
}

int get()
{
	int x=dui[1],i=1;
	dui[1]=dui[tot];
	dui[tot]=0;
	tot--;
	while (1)
	{
		int l=i*2,r=i*2+1,wz;
		if (!((p[dui[i]]>p[dui[l]]&&l<=tot)||(p[dui[i]]>p[dui[r]]&&r<=tot))) break;
		if (r>tot||p[dui[l]]<p[dui[r]]) wz=l; else wz=r;
		swap(dui[i],dui[wz]);
		i=wz;
	}
	return x;
}

int findup(int x)
{
	for (int i=js(deep[x]);i>=0;i--)
		if (bz[f[x][i]]==true) x=f[x][i];
	return x;
}

int main()
{
	int n,t;
	scanf("%d%d",&n,&t);
	for (int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		a[x].push_back(y);
		a[y].push_back(x);
	}
	for (int i=1;i<=n;i++)
	{
		b[i]=i;
		sort(a[i].begin(),a[i].end());
	}
	dfs(1,0);
	
	for (int j=1;j<=js(n);j++)
		for (int i=1;i<=n;i++)
			f[i][j]=f[f[i][j-1]][j-1];
			
	sort(b+1,b+n+1,cmp);
	for (int i=1;i<=n;i++)
		p[b[i]]=i;
	for (int i=1;i<=n;i++)
		insert(i);
	
	for (int i=1;i<=t;i++)
	{
		int op,x;
		scanf("%d%d",&op,&x);
		if (op==1)  
		{
			int w;
			for (;x;x--)
			{
				w=get();
				bz[w]=true;
			}
			printf("%d\n",w);
		} else
		{
			int y=findup(x);
			printf("%d\n",deep[x]-deep[y]);
			insert(y);
			bz[y]=false;
		}
	}
	return 0;
}