回归模型中残差非正态性的诊断与处理

作为一名数据分析师或科研人员，线性回归无疑是你武器库中最常用、最强大的工具之一。我们熟练地操作软件，得到一长串结果，然后迫不及待地看向那个决定性的p值，以此判断模型的“成功”与否。然而，一个严谨的分析师都知道，p值并非审判模型的唯一法官，模型背后的基本假设——尤其是残差的正态性——才是保证所有统计推断（如系数检验、置信区间）稳健可靠的基石。

我们会在SPSSAU等软件中进行线性回归分析，可勾选“保存残差和预测值”进行正态性检验。但当检验结果无情地显示p < 0.05，即残差拒绝服从正态分布时，我们该怎么办？是模型失效了，还是数据本身有问题？本文将带你深入问题的核心，提供一套从诊断到修复的完整行动方案。

一、 为什么线性回归要求残差服从正态分布？

简单来说，线性回归模型可以表示为：Y = β₀ + β₁X₁ + ... + βₖXₖ + ε。这里的 ε 就是我们常说的随机误差项，或残差。它代表了模型无法解释的部分。我们对于回归系数 β 的显著性检验（t检验、F检验），以及构建置信区间，在数学推导上都基于一个核心假设：这些残差 ε 是独立同分布，且服从均值为0、方差为常数的正态分布。

如果这个假设不成立，会产生什么后果？

1. 系数检验失效：我们计算出的p值可能不再准确。原本不显著的变量可能变得“显著”，或者反之，导致我们做出错误的科学结论。
2. 置信区间失准：我们构建的95%置信区间可能不再是真正的95%，其覆盖真实参数的概率会发生变化，区间估计变得不可靠。
3. 模型预测偏差：在进行预测时，预测区间会变得不准确，无法真实反映预测值的不确定性。

因此，检验残差的正态性并非可有可无的“走过场”，而是模型诊断中至关重要的一环。

二、 诊断：如何系统地检验残差的正态性？

在SPSSAU中，我们可以在进行线性回归时，直接勾选“保存残差和预测值”的选项。分析结束后，SPSSAU会在我们的原始数据中生成两列新的数据：残差和预测值。接下来，我们就可以利用这些保存下来的残差进行系统的正态性检验。

一个完整的诊断流程，应该结合图形观察和统计检验，如下图所示：

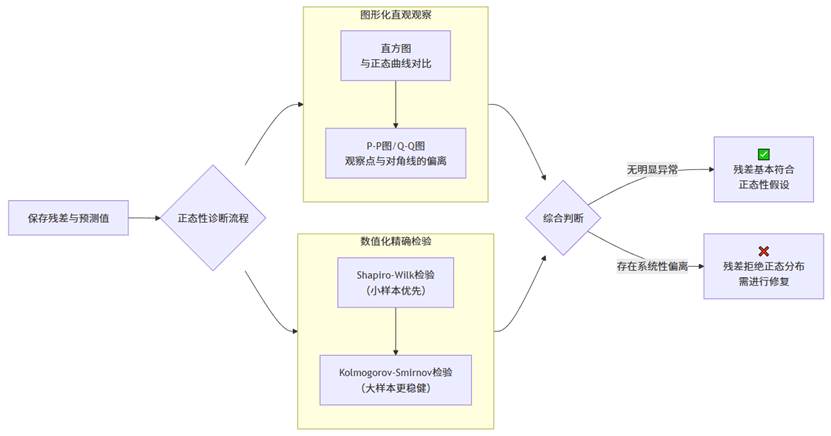
我们的诊断流程分为“图形法”和“统计检验法”两条路径。

• 图形法（如直方图、P-P/Q-Q图） 的优势在于直观，能帮助我们识别非正态的具体模式（如偏态、尖峰、离群点）。
• 统计检验法（如S-W检验、K-S检验） 则提供一个客观的数值标准。最终需要将两者结合，做出综合判断。如果图形显示有明显偏离，或统计检验p值小于显著性水平（如0.05），则判定为残差非正态。

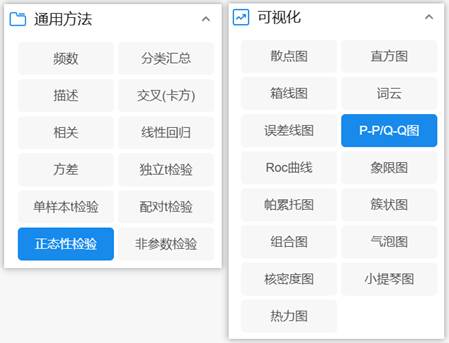
SPSSAU操作：在SPSSAU的“可视化”栏目中，你可以轻松绘制残差的直方图、P-P图或Q-Q图。同时，在“通用方法”的“正态性检验”中，将残差项拖入分析框，即可得到S-W或K-S检验的结果。这种一体化的流程设计，极大地简化了我们的诊断工作。

三、 修复：当残差非正态时，我们有哪些选择？

诊断出问题只是第一步，更重要的是如何修复。面对非正态的残差，我们绝不能简单地忽略它。以下是一套从易到难、从数据到模型的系统性解决路径。

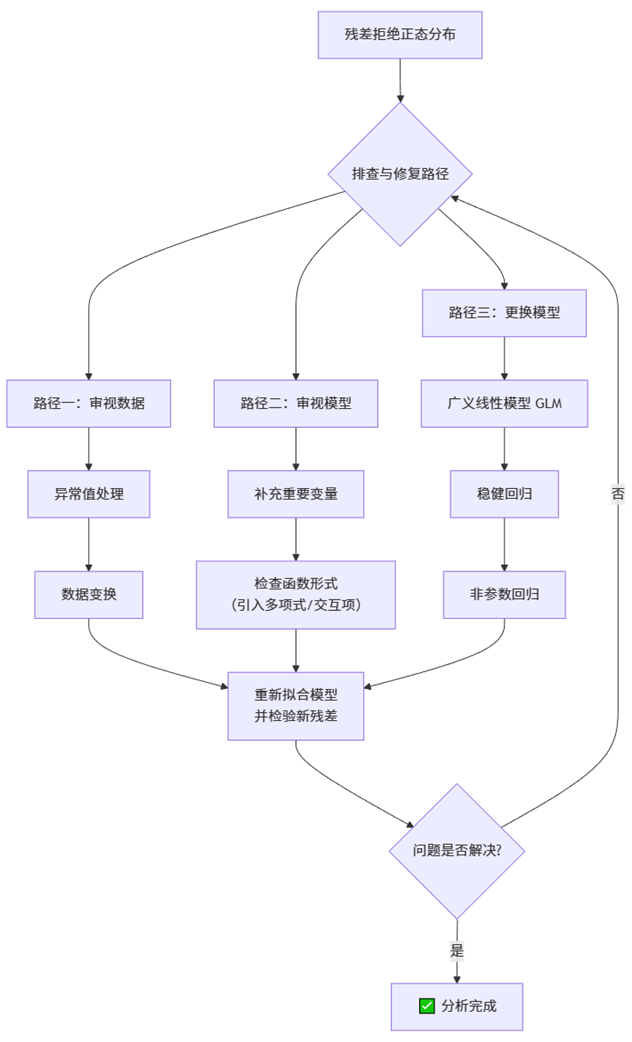
这是一个迭代的修复过程。我们首先从最简单的数据层面入手，检查异常值和进行变量变换。如果无效，则考虑模型设定，看看是否遗漏了重要变量或错误的函数形式。若问题依然存在，则可能需要彻底更换模型框架，放弃普通最小二乘法（OLS），转向更高级的模型。每一步操作后，都需要重新拟合模型并检验新残差，直到问题解决。

下面，我们详细展开每一条路径：

路径一：审视与处理数据

（1）异常值处理：

一个或几个极端的离群值会严重扭曲回归线，导致残差分布出现拖尾，破坏正态性。绘制残差与预测值的散点图，观察是否有明显远离主体数据分布的点。谨慎地检查这些异常值。如果是录入错误，则修正；如果是特殊个案（如公司CEO的薪资），可以考虑将其单独分析或使用虚拟变量控制；如果确实是非代表性极端值，在充分说明理由后可以剔除。切记，剔除数据必须有理有据，并报告处理过程。

（2）数据变换：
这是处理非正态残差（特别是偏态分布）和最常用的方法之一。通过对因变量Y进行数学变换，可以改变其尺度，使数据更符合线性模型的假设。

• 对数变换（Log Transformation）：适用于右偏分布（大量小值，少数极大值）的数据，如收入、房价、人口等。公式：Y_new = log(Y)。如果数据含0，可用 log(Y+1)。
• 平方根变换（Square Root Transformation）：适用于轻度右偏的计数数据。
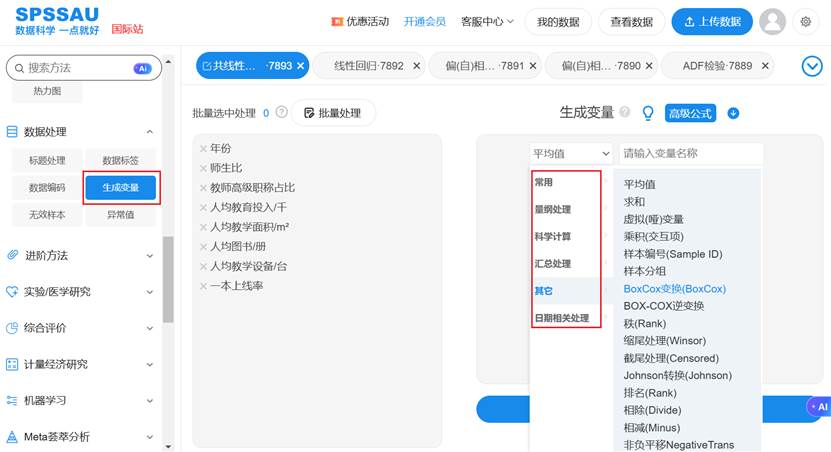
• Box-Cox变换：一种自动选择最佳变换参数的强大方法。它能找到一个λ值，使得变换后的数据 (Y^λ - 1)/λ 最接近正态分布。SPSSAU【生成变量】算法可以一键生成变换后的新变量，非常方便。

路径二：审视与修正模型设定

很多时候，残差的非正态性源于模型本身的设定错误，即“错误的模型”拟合了“真实的关系”。

（1）遗漏重要变量：

问题：如果模型中遗漏了一个与当前自变量相关的关键解释变量，那么这个被遗漏变量的影响就会被迫进入残差项中，导致残差出现系统性模式（而非随机），从而破坏正态性。

解决：基于领域知识，重新审视模型，考虑是否有可能遗漏了重要的预测变量，并将其加入模型。

（2）错误的函数形式：

问题：真实世界的关系未必是直线。如果我们用直线 Y = a + bX 去拟合一个曲线关系（如 Y = a + bX + cX²），那么模型无法解释的非线性部分就会进入残差，造成非正态。

诊断：绘制残差与预测值的散点图。如果 points 呈现明显的曲线 pattern（如U型或倒U型），则暗示存在非线性。

解决：在模型中加入自变量的高阶项（如 X²）、或进行分段回归。也可以考虑对自变量进行变换。

路径三：更换建模框架——放弃OLS

如果以上方法都无法奏效，我们可能需要承认数据本身就不适用于经典的线性回归（OLS），此时应转向更强大的模型。

（1）广义线性模型（GLM）：

核心思想：GLM放宽了“因变量必须连续且正态”的严格限制。它通过一个“连接函数”，将因变量的期望值与自变量的线性组合联系起来，并允许残差服从指数族分布（包括正态、泊松、二项分布等）。

应用场景：如果因变量是计数数据（如一年内发病次数），残差很可能呈泊松分布，应使用泊松回归。如果因变量是二分类数据（如成功/失败），应使用Logistic回归。如果因变量是比例数据（如市场份额），应使用Beta回归。

SPSSAU支持：在“进阶方法”栏目中，SPSSAU提供了丰富的GLM模型，如Logistic回归、泊松回归等，可以轻松应对不同类型的因变量。

（2）稳健回归（Robust Regression）：

这类方法不直接处理非正态性，而是通过降低异常值在估计回归系数时的权重，来得到一个受异常值影响更小的、更稳健的模型。即使残差非正态，它也能给出相对可靠的系数估计。当你认为数据中存在异常值，但又无法或不希望将其剔除时，稳健回归是极佳的选择。

（3）非参数回归：

当对数据分布和关系形式完全未知时，可以考虑使用非参数方法，如核回归、局部加权回归等。它们对模型假设的要求极低，但计算复杂且结果解释性稍差。

四、 实例演示：在SPSSAU中完成完整流程

假设我们研究公司销售额与广告投入的关系，建立线性回归模型后，保存残差。

1. 诊断：对残差进行S-W检验，p值为0.003 (<0.05)，拒绝正态性假设。同时，残差直方图呈现明显的右偏。
2. 修复：由于销售额通常为正且可能右偏，我们尝试对因变量“销售额”进行对数变换。在SPSSAU中，使用【数据预处理->生成变量】功能，输入公式ln(销售额)，创建新变量。
3. 重新建模：以ln(销售额)为新因变量，广告投入为自变量，重新进行线性回归，并再次保存新残差。
4. 再次诊断：对新残差进行正态性检验，发现S-W检验p值变为0.125 (>0.05)，且直方图和Q-Q图都显示接近正态分布。问题得到完美解决。
5. 结果解释：此时，我们的模型是一个“对数-线性”模型，回归系数的解释需要变化：广告投入每增加1个单位，销售额平均增加 (exp(b) - 1) * 100%。

五、 总结

面对回归模型中残差不服从正态分布的问题，我们绝不应束手无策或视而不见。一个严谨的数据分析师应当像一位侦探，遵循一套系统的流程：

• 第一步，确证：利用SPSSAU等工具，通过图形和统计检验，确凿地诊断问题。
• 第二步，溯源：从数据（异常值、分布）和模型（变量遗漏、形式错误）两个层面追溯问题根源。
• 第三步，修复：根据溯源结果，选择最合适的策略——从简单的数据变换，到复杂的模型更替。

记住，一个好的模型，不在于它的结果看起来多么“显著”，而在于它是否真实、稳健地反映了数据背后的故事。而确保残差“听话”，正是我们讲好这个故事的关键前提。