分层回归分析全解析：SPSSAU带你掌握模型构建与因果推断

一、分层回归：什么是“分层”？为何要“回归”？

分层回归（Hierarchical Regression）是多元线性回归的拓展形式，通过分阶段引入自变量来考察每个变量集对因变量的独特贡献。与传统回归不同，分层回归强调变量引入的理论顺序与逻辑层次，广泛应用于心理学、管理学、经济学等领域的因果机制探索。

SPSSAU的分层回归模块实现了流程化、可视化的分析体验，用户只需设定分层顺序，系统即可自动完成模型比较、贡献度分解与结果解读，极大降低了方法应用的门槛。

下面通过一个完整的分析流程图，展示SPSSAU中分层回归的实现路径：

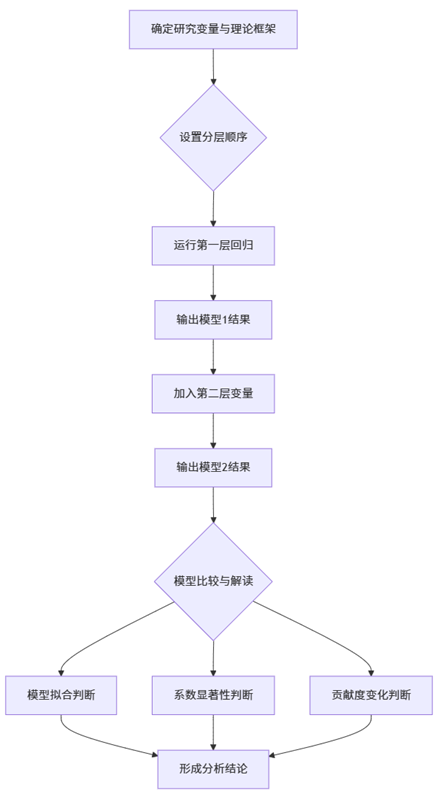
流程解读：分析伊始，研究者需明确因变量与自变量，并基于理论或研究假设确定变量引入的层级顺序。SPSSAU依次运行各层回归，并输出每层的模型拟合指标、系数估计与统计检验结果。最后，通过比较层间变化，判断新增变量的贡献与模型的优化程度。

二、分层回归的核心指标系统：从模型拟合到系数解读

SPSSAU的分层回归输出包含丰富的统计指标，可分为模型拟合指标、回归系数指标与模型比较指标三大类。理解这些指标的含义与关联，是正确解读结果的关键。

1. 模型拟合指标

拟合指标反映模型整体对数据的解释力，主要包括：

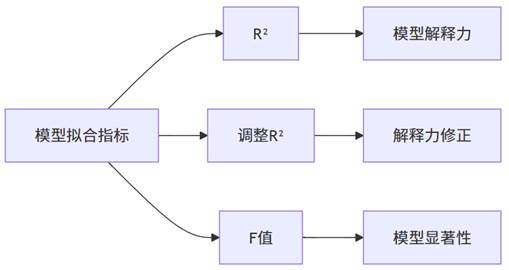
• R²（决定系数）：反映模型所有自变量共同解释的因变量方差比例。R²越高，模型拟合度越好。
• 调整R²：考虑自变量个数后的修正R²，防止因变量增加而虚假提高解释力。
• F值：检验模型整体显著性的统计量，对应p值若小于0.05，表明模型显著成立。

2. 回归系数指标

系数指标考察每个自变量的独立影响：

指标	含义与解读
非标准化系数(B)	自变量每变化1单位，因变量的原始变化量
标准化系数(β)	消除量纲后的影响强度，可用于比较变量重要性
t值	系数显著性检验统计量
p值	若p<0.05，表明该自变量影响显著
VIF值	方差膨胀因子，检验多重共线性（通常<5即可）

3. 模型比较指标

比较指标用于评估新增变量的贡献：

指标	含义
△R²	新增变量带来的R²增加量
△F值	检验△R²显著性的统计量

SPSSAU输出分层回归部分结果示例如下：

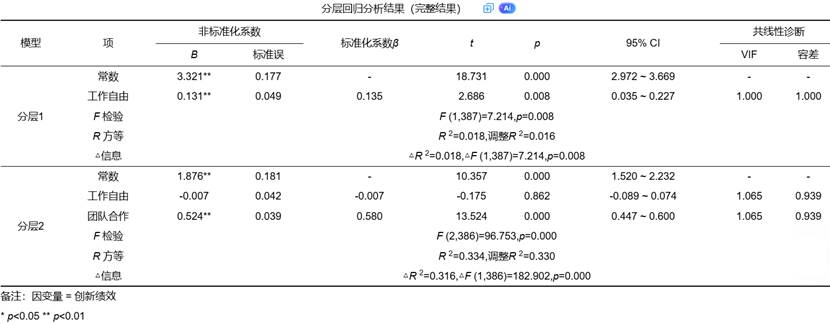
三、模型结构的逻辑关系

以 SPSSAU 报告为例，模型结构可以抽象为以下层次逻辑：

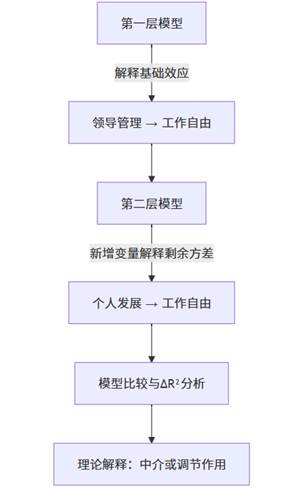
理论层面解释：

1. 第一层模型 通常放入控制变量或核心预测变量；
2. 第二层模型 加入新的自变量、调节变量或中介变量；
3. 若第二层模型显著改善解释力，则表明新变量具有“额外贡献”。

这种“层层推进”的设计，使研究者能分清：哪些变量是“基础影响”，哪些是“增量影响”。

四、分层回归在中介与调节分析中的作用

除了传统的模型构建，分层回归更是中介效应与调节效应检验的基础方法。SPSSAU为这两类分析提供了专用模块【问卷研究】模块->【调节作用】【中介作用】分析，大幅简化了检验流程。

1. 中介效应检验

中介效应考察“X如何通过M影响Y”的机制问题。使用分层回归进行中介检验的步骤如下：

• 步骤1：建立X对Y的回归（总效应）
• 步骤2：建立X对M的回归
• 步骤3：建立X和M对Y的回归（直接效应）
• 判断准则：若步骤1、2、3中X系数均显著，且步骤3中M系数显著，则存在中介效应。

1. 调节效应检验

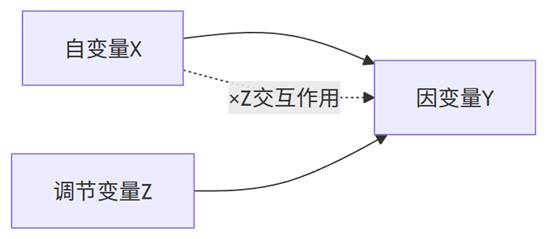
调节效应考察“W如何影响X与Y之间的关系”的边界条件。分层回归中的检验步骤：

• 步骤1：建立X和W对Y的回归
• 步骤2：加入X与W的交互项（乘积项）
• 判断准则：若交互项系数显著，则调节效应存在。

SPSSAU的调节效应模块自动完成中心化、乘积项生成与简单斜率分析，使这一复杂过程变得简单易行。

五、指标体系分类与关系梳理

分类	指标	理论意义	相互关系
模型拟合指标	R²、调整R²、F值	衡量模型整体解释力	随变量增多而变化，用于层间比较
增量效应指标	ΔR²、ΔF	衡量新变量引入的贡献	反映第二层相对于第一层的改进
显著性检验	t值、p值	判断自变量对因变量的影响是否显著	与回归系数共同解释影响强度
回归系数	B、β	描述影响方向与大小	β用于比较变量影响权重
稳定性诊断	VIF、容差	检测多重共线性问题	过高VIF提示变量冗余或相关性过强
数据有效性	样本量、有效样本率	确保分析结果可靠	有效样本为模型建立基础

这些指标相互关联，共同构成一个从“数据质量—模型拟合—显著性检验—稳定性诊断”的闭环体系。

七、SPSSAU的智能化分层分析体验

在传统统计软件中（如SPSS、Stata、R），分层回归需要手动建立多个模型、计算ΔR²与ΔF、生成VIF表格，整个过程繁琐且易出错。

而在 SPSSAU 平台：上传数据 → 选择“分层回归”；设定分层顺序（拖拽即可）；点击“开始分析”，即可得到全套报告。SPSSAU分层回归操作示例如下图：

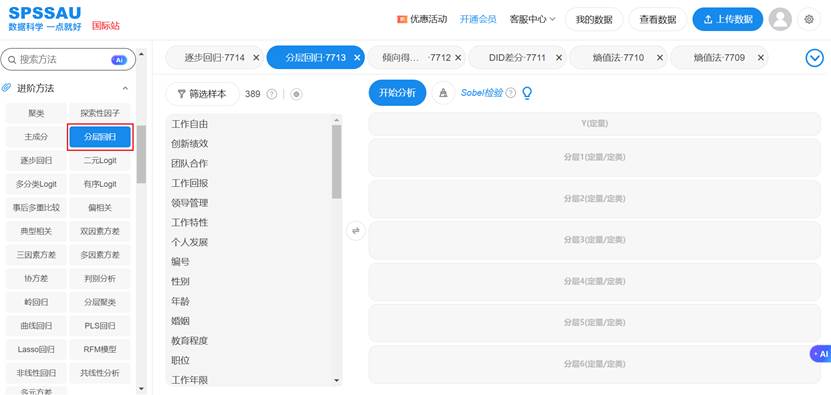
分层回归通过分层次、递进式的模型构建策略，使研究者能够基于理论假设，系统考察变量集的独立贡献与增量效度。它不仅是一种统计技术，更是一种研究思维——强调变量引入的理论依据与逻辑顺序。

SPSSAU将这一复杂方法转化为直观、易用的分析流程，使研究者能够专注于理论构建与结果解读，而非计算细节。无论你是正在进行学术研究，还是从事商业分析，SPSSAU都能为你提供专业、可靠、高效的分层回归分析支持。