最大方差法和最优斜交法在因子分析中的区别是什么？

在社会科学、心理学、市场研究等领域，因子分析是一种常用的多变量统计方法，用于探索数据集中的潜在结构。它通过降维技术，将多个观测变量简化为少数几个因子，从而揭示变量之间的内在关联。然而，因子分析的结果往往依赖于旋转方法的选择，其中最大方差法（Varimax）和最优斜交法（Promax）是两种广泛应用的旋转技术。本文将从基础概念出发，深入探讨这两种方法的原理、流程、区别及实际应用，并结合SPSSAU软件的操作示例，帮助读者在研究中做出更明智的选择。

一、因子分析基础：为什么需要旋转？

因子分析的核心在于从原始变量中提取公共因子，这些因子能够解释数据中的大部分方差。在EFA中，初始因子解往往难以解释，因为因子载荷矩阵可能显示多个变量在多个因子上都有较高载荷，导致因子结构模糊。这时，因子旋转就显得至关重要。

因子旋转通过调整因子轴的方向，使因子载荷矩阵更易于解释。旋转方法主要分为两类：正交旋转和斜交旋转。正交旋转假设因子之间不相关，而斜交旋转允许因子之间存在相关关系，这更符合现实世界中变量的复杂性。最大方差法是一种典型的正交旋转方法，而最优斜交法则属于斜交旋转的范畴。选择哪种旋转方法，取决于研究假设和数据特性。例如，在SPSSAU进行探索性因子分析时，用户可以在分析前灵活选择这两种旋转方法，以确保结果的可解释性和准确性。

二、最大方差法：正交旋转的经典之选

最大方差法（Varimax）由Kaiser于1958年提出，是一种最常用的正交旋转方法。其核心思想是最大化因子载荷矩阵的方差，使得每个变量在尽可能少的因子上有高载荷，从而简化因子结构。这种方法适用于因子间相互独立的假设，常用于心理学或教育测量中，其中潜在特质被视为不相关的。

最大方差法的原理与步骤

最大方差法通过数学优化，调整因子载荷矩阵，使每个因子的载荷平方的方差最大化。具体来说，它强调“简单结构”——即每个变量只在一个因子上有高载荷，而在其他因子上载荷接近零。这有助于提高因子的可解释性。

最大方差法的优点在于其简单性和稳定性。由于假设因子正交，结果易于解释和报告，尤其适用于初学者的研究。然而，它的局限性也很明显：如果真实数据中因子之间存在相关性，最大方差法可能强行将不相关的因子分离，导致结果失真。例如，在人格测验中，如果“外向性”和“开放性”因子实际相关，使用最大方差法可能掩盖这种关联，从而影响理论的构建。

在实际应用中，最大方差法常与主成分分析结合，用于量表开发或维度缩减。根据SPSSAU的文档，该方法在因子分析中的计算效率高，适合大规模数据集。但用户需注意，如果因子间相关性较高（例如，相关系数大于0.3），则可能需要考虑斜交旋转方法。

三、最优斜交法：斜交旋转的灵活替代

最优斜交法（Promax）是一种高效的斜交旋转方法，由Hendrickson和White于1964年提出。它通过先进行正交旋转（如最大方差法），再施加斜交变换，允许因子之间相关。这种方法更适用于现实世界中的复杂数据，其中潜在因子往往不是完全独立的，例如在社会科学或生物学研究中。

最优斜交法的原理与步骤

最优斜交法的核心是追求“最优”简单结构，同时容忍因子间的相关性。它使用一个参数（通常称为“幂”参数）来控制旋转的斜交程度：值越高，旋转越斜交，因子结构越简单，但可能过度拟合；值越低，则更接近正交旋转。最优斜交法通常分两步：首先应用最大方差法获得初始解，然后通过最小化目标函数来调整因子轴，使载荷矩阵更接近简单结构。

最优斜交法的优势在于其灵活性：它能够捕捉因子之间的自然关联，提高模型的现实适用性。例如，在市场细分研究中，消费者态度因子可能相互影响，使用最优斜交法可以更准确地反映这种复杂结构。然而，它的缺点也很突出：因子相关矩阵的引入增加了结果解释的难度，且可能因过度拟合而导致不稳定。此外，最优斜交法对参数选择敏感，在SPSSAU中，软件通常提供默认参数，但高级用户可以根据数据特性调整幂值以优化结果。

从计算角度看，最优斜交法比最大方差法更复杂，但在现代统计软件如SPSSAU中，这一过程已高度自动化。用户只需在探索性因子分析前选择“Promax”，即可获得详细的输出，包括因子载荷和因子间相关系数，从而进行深入分析。

四、最大方差法与最优斜交法的核心区别

在理解了两种方法的基本原理后，我们可以从多个维度对比它们的区别。这些区别不仅影响方法的选择，还直接关系到研究结论的可靠性。

1. 理论基础：正交vs斜交

最大方差法基于正交假设，因子轴相互垂直，因子间相关系数为零。这简化了模型，但可能不符合现实；最优斜交法则基于斜交假设，允许因子相关，更灵活但复杂。例如，在心理学中，如果研究假设人格特质独立，最大方差法更合适；但如果特质间存在重叠（如焦虑和抑郁），最优斜交法更能反映真实情况。

2. 结果解释与简单结构

最大方差法通过最大化方差，倾向于产生“干净”的因子载荷矩阵，每个变量明显归属于一个因子，解释直观。最优斜交法虽然也追求简单结构，但由于因子相关，载荷矩阵可能显示变量在多个因子上的交叉载荷，解释时需要同时考虑因子相关矩阵。在SPSSAU的输出中，最大方差法通常提供旋转后的因子载荷表，而最优斜交法则额外提供因子相关矩阵，帮助用户评估因子间关系。

3. 适用场景与数据特性

最大方差法适用于因子间独立性高的数据，例如标准化测试或理论驱动的研究；最优斜交法则更适合探索性研究，其中因子关系未知或已知相关。根据SPSSAU的用户指南，如果因子间相关系数低于0.3，最大方差法可能足够；但如果高于0.3，建议尝试最优斜交法以避免偏差。

4. 计算复杂性与稳定性

最大方差法计算简单、稳定，不易受数据噪声影响；最优斜交法由于迭代优化和参数依赖，可能对异常值敏感，但在大样本中通常稳健。在SPSSAU中，两种方法都经过优化，确保快速计算，但用户应注意样本量建议（通常n>100）。

5. 实际应用中的选择

在实践中选择旋转方法时，研究者应考虑研究目标、理论框架和数据探索结果。SPSSAU在探索性因子分析模块中提供了这两种选项，并附带解释说明，帮助用户根据KMO检验、Bartlett球形检验等指标做出决策。例如，如果初步分析显示因子相关性显著，切换到最优斜交法可能改善模型拟合。

五、SPSSAU实践指南：如何应用这两种旋转方法

SPSSAU作为一款用户友好的在线统计分析工具，简化了因子分析的过程，包括旋转方法的选择。以下是一个简要的操作示例，展示如何在SPSSAU中应用最大方差法和最优斜交法。

首先，用户上传数据后，进入“探索性因子分析”模块。在参数设置中，旋转方法选项包括“最大方差法（Varimax）”和“最优斜交法（Promax）”。选择前者时，SPSSAU会自动执行正交旋转，输出因子载荷矩阵和方差解释率；选择后者时，软件会先进行初始正交旋转，再应用斜交变换，输出载荷矩阵和因子相关矩阵。

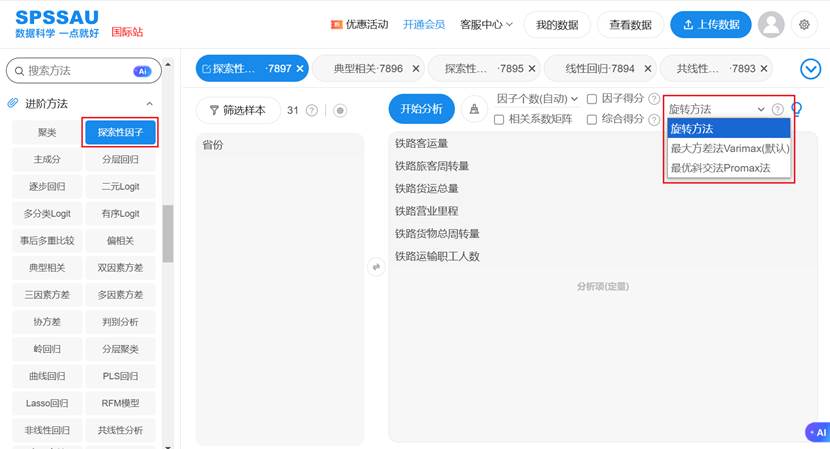
例如，在一项市场研究中，用户可能使用SPSSAU分析消费者问卷数据。如果初始分析显示因子间相关性低，选择最大方差法可得到清晰的品牌态度因子；但如果因子如“价格敏感度”和“品质追求”相关，则最优斜交法能提供更真实的洞见。SPSSAU的输出还包括图表和拟合指标，如累积方差贡献率，帮助用户评估旋转效果。