正态性检验全流程深度解析：统计检验、图示检验、峰度偏度

一、引言：正态性检验的重要性

正态性检验是统计学中的基础性工作，在参数检验、回归分析、质量控制和科学研究中具有举足轻重的地位。数据是否服从正态分布，直接关系到统计方法的选择和结论的可靠性。作为一款专业的统计分析平台，SPSSAU为用户提供了完整的正态性检验解决方案，涵盖从图形观察到统计检验的全套方法，让这一复杂过程变得简单而高效。

正态分布又称高斯分布，是自然界和社会现象中最常见的分布形式。许多统计方法如t检验、方差分析、线性回归等都建立在数据正态分布的假设基础上。因此，在进行这些分析前，进行正态性检验是必不可少的步骤。SPSSAU通过智能化的分析流程和丰富的输出结果，帮助用户全面评估数据的分布特性，为后续分析奠定坚实基础。

二、正态性检验方法体系

SPSSAU中的正态性检验形成了完整的方法体系，用户可以根据研究需求和数据特点选择合适的方法。以下是正态性检验的完整分析框架：

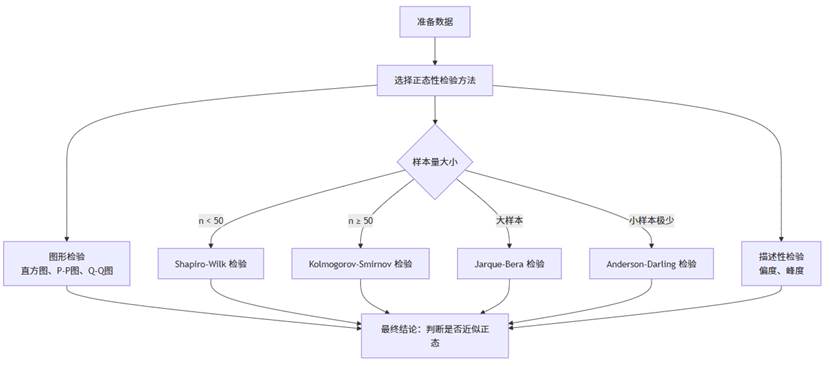
这张图展示了在真实分析中推荐采用的“多方法交叉验证”流程。统计检验、图示、偏度峰度各有优劣。SPSSAU 正是按照这样的逻辑，将统计检验与图示检验同步输出，方便用户形成综合判断，而不是盲目依赖单一 p 值。

三、正态性检验方法分类详解

3.1 正态性统计检验方法

统计检验方法通过计算特定的统计量并对分布假设进行检验，提供客观的判据标准。SPSSAU提供四种主要的正态性检验方法，各具特色，适用于不同场景。

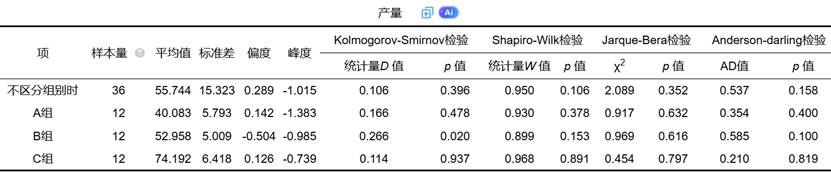
（1）Kolmogorov-Smirnov检验（K-S检验）

基于经验分布函数与理论分布函数的比较，适用于大样本情况。其检验统计量D值表示两个分布函数之间的最大垂直距离，当D值对应的p值大于显著性水平时，接受正态性假设。

（2）Shapiro-Wilk检验

被认为是检验功效最强的正态性检验方法之一，特别适用于小样本场合（通常n<50）。该检验通过计算数据与理论值的相关性来评估正态性，W统计量越接近1，表明数据越符合正态分布。

（3）Jarque-Bera检验

基于样本偏度和峰度的联合检验，在大样本情况下具有良好性质。该检验本质上是通过比较样本偏度、峰度与正态分布的期望值（偏度为0，峰度为3）的差异来构建检验统计量。

（4）Anderson-Darling检验

是K-S检验的改进版本，对分布的尾部差异更为敏感，在样本量较少时（如n<25）仍保持较好的检验功效。该检验通过加权的方式更加关注分布两端的拟合情况。

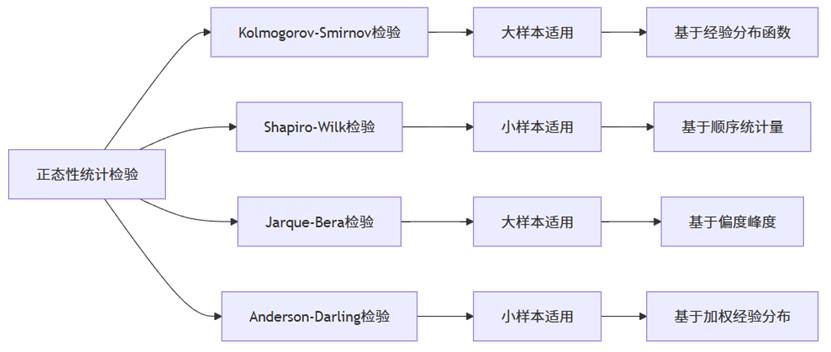
各种正态性检验方法基于不同的统计原理，适用于不同的样本规模。K-S检验和Anderson-Darling检验基于经验分布函数理论，通过比较样本累积分布与理论累积分布的差异来检验正态性；Shapiro-Wilk检验基于顺序统计量的相关性，特别适合小样本情况；Jarque-Bera检验则从分布形态的偏度和峰度特征入手，在大样本情况下效果良好。SPSSAU同时提供这四种方法，让用户能够根据自身数据特点选择最合适的检验方式，或通过多种方法相互印证，提高判断的准确性。

3.2 可视化图形检验方法

图形化方法通过视觉直观地展示数据分布特征，是正态性检验中不可或缺的组成部分。SPSSAU提供三种主要的图形工具，从不同角度呈现数据分布信息。

（1）直方图

是最直观的分布展示工具，通过矩形高度表示频数，可以快速了解数据的集中趋势、离散程度和分布形态。在直方图上叠加正态分布曲线，可以直观比较数据分布与理论正态分布的吻合程度。

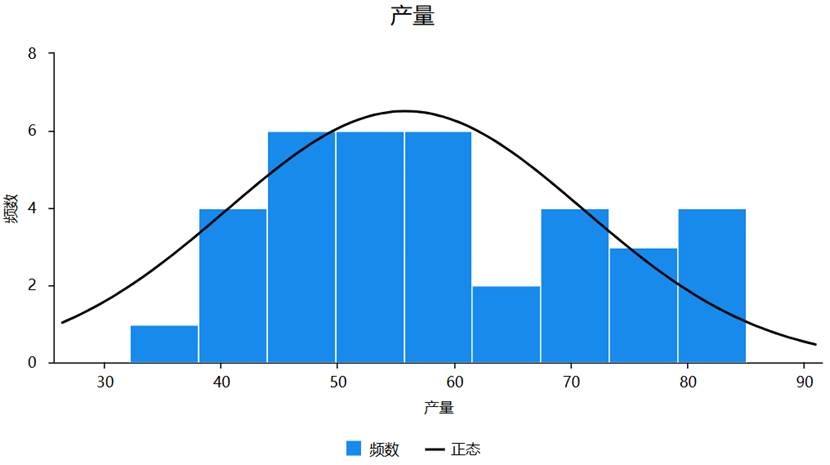
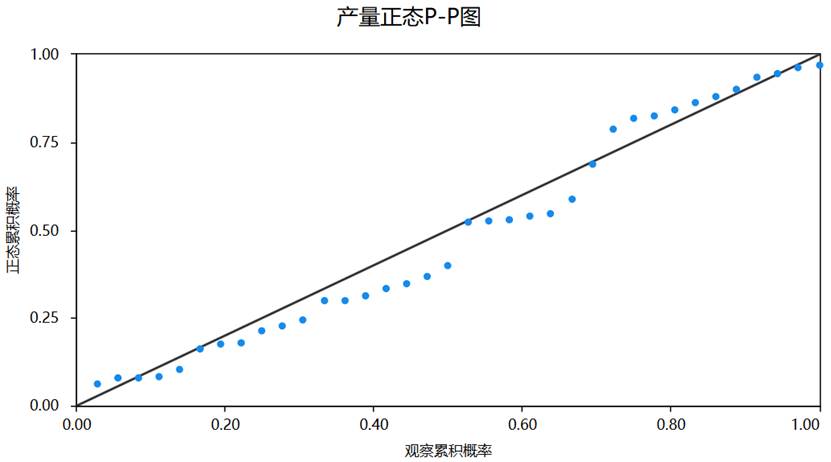
（2）P-P图（概率-概率图）

通过比较样本累积比例与理论正态分布累积比例的一致性来检验正态性。如果数据服从正态分布，散点应当近似分布在一条对角直线上。P-P图对分布中间部位的拟合情况较为敏感。

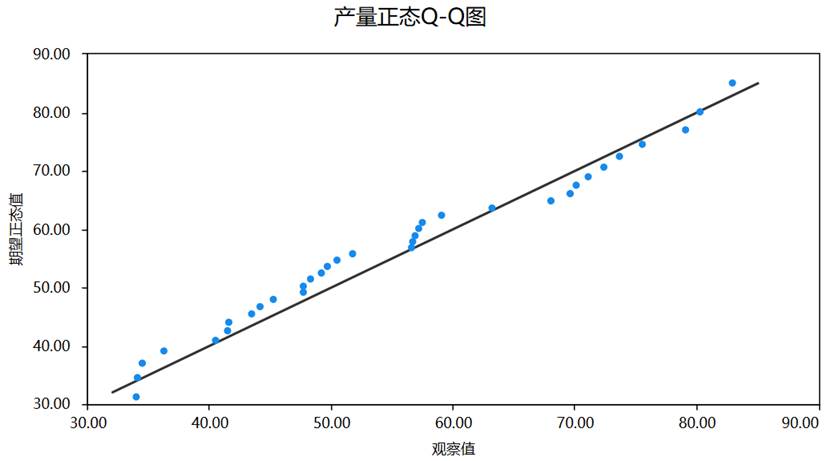
（3）Q-Q图（分位数-分位数图）

是另一种重要的正态性诊断工具，通过比较样本分位数与理论正态分布分位数的关系来评估正态性。与P-P图相比，Q-Q图对分布尾部的差异更加敏感，能够更好地检测极端值与正态分布的偏离。

3.3 峰度偏度检验法

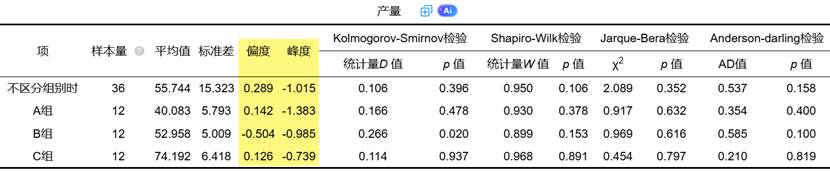
峰度和偏度是描述分布形态的重要指标，为正态性检验提供补充信息。

（1）偏度衡量分布不对称性的方向和程度。正偏度表示分布右侧有长尾，负偏度表示分布左侧有长尾，而对称分布的偏度接近0。正态分布是对称分布，偏度理论上为0。

（2）峰度描述分布形态的陡峭程度，反映数据在均值附近的集中程度。高峰度表示分布比正态分布更陡峭，低峰度表示分布比正态分布更平坦。正态分布的峰度理论上为3（超额峰度为0）。

通过偏度和峰度的联合分析，可以初步判断数据分布与正态分布的形态差异，一般认为如果峰度绝对值小于10并且偏度绝对值小于3，则说明数据虽然不是绝对正态，但基本可接受为正态分布。

四、总结

正态性检验的目的从来不是单纯“看 p 值”，而是：

• 明确数据是否满足参数检验前提
• 判断是用 t 检验还是非参数检验
• 判断是否要对数据进行变换
• 理解数据形态及其背后机制

而 SPSSAU 之所以更适合论文和科研，是因为它把所有结果整合在一张表里，并自动提供图示与建议，让用户无需反复查书、查文档，大幅提升效率。