正交试验设计，正交表生成与极差分析

在工程优化、工艺改进、新材料研发等领域，我们常常面临这样的困境：影响结果的因素众多，每个因素又有多个可能取值。如果对所有可能的组合进行“全面实验”，其工作量将是天文数字。例如，仅对一个7因素3水平的工艺进行探究，全面实验就需要进行 3^7 = 2187 次！这在实际中几乎无法实现。

那么，是否存在一种方法，能从这浩如烟海的组合中，智能地挑选出一小部分最具代表性的实验，从而高效、准确地锁定关键因素和最优参数？答案是肯定的。正交试验设计 正是为解决这一“多因素优化”难题而生的强大统计学工具。

本文将系统解析正交试验设计的核心思想、关键工具——正交表，以及分析实验结果的两大方法：直观的极差分析与严谨的方差分析，助你掌握这套化繁为简的科研与工程利器。

一、正交试验

在深入细节之前，我们必须理解正交试验要解决的核心矛盾：因素的多样性与实验资源的有限性。传统“每次只改变一个因素”的方法（即控制变量法）效率低下，且无法考察因素间的交互作用；而全面实验法则因成本过高而不可行。

正交试验设计的基本思路，是在均衡分散与整齐可比两大原则指导下，从全面实验点中选取一部分有代表性的点进行实验。这部分实验点构成的集合，虽然数量很少，却能提供关于各个因素及其水平对结果影响的丰富信息。

整个过程遵循一个清晰的逻辑闭环，我们可以通过下图一览其全貌：

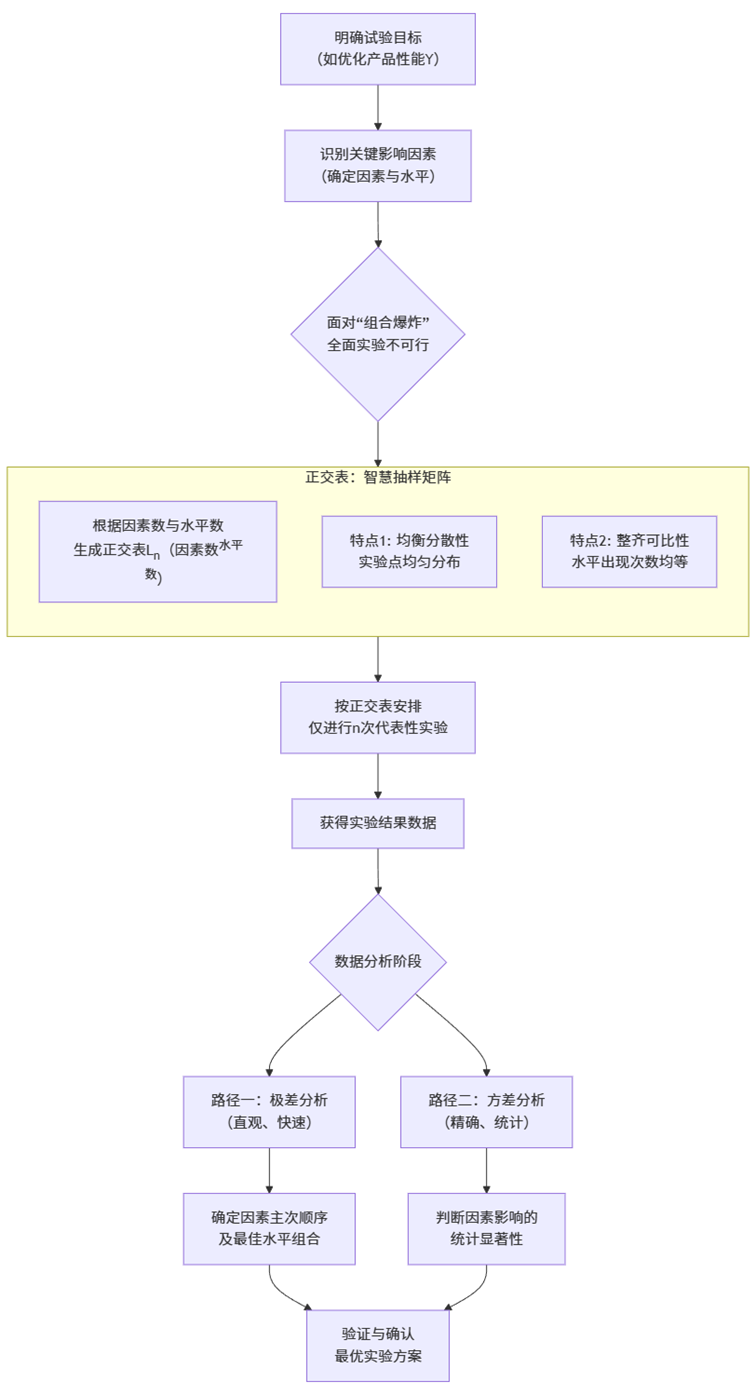
如图所示，正交试验设计如同一座桥梁，连接了复杂的问题空间与可行的解决方案。它的起点是明确的目标与因素分解，终点是经过数据验证的最优方案。接下来，我们将深入剖析这座桥梁的核心构件——正交表。

二、正交表

正交表是正交试验设计的灵魂，它是一种依据组合数学与数理统计原理预先编制好的标准化表格。其表现形式通常为 Lₙ（因素数^水平数），例如 L₉（3⁴）表示一个需要做9次实验，最多可安排4个3水平因素的表。

正交表的两大基石性质

1. 均衡分散性（均匀性）： 这是正交表最精妙之处。它保证所选取的实验方案（即表中的每一行）在全部可能的实验方案中均匀分布。用几何语言描述，如果将每个因素作为一个坐标轴，每个水平作为一个刻度，那么全面实验点构成一个高维网格。正交表所选的实验点，就像在这个高维网格中均匀撒下的“采样点”，没有任何区域被过分集中或忽略。这意味着，这一小部分实验能够最大限度地“代表”全局。
2. 整齐可比性（正交性）： 这是进行科学比较的基础。对于正交表中任意一列（即某一个因素），它的各个水平出现的次数是相同的；对于任意两列（即任意两个因素），它们的不同水平组合出现的次数也是相同的。这带来的巨大好处是：当我们在比较某个因素不同水平的优劣时，其他因素的影响是“平等”地作用于各个水平的。换言之，其他因素的效应在比较中被“抵消”了，从而可以清晰、无偏地估计出该因素自身的效应。这就好比在比较两种肥料的效果时，确保使用这两种肥料的土地在其他条件（如光照、水分）上完全一致。

正交表的生成与灵活性

需要明确的是，对于给定的因素数和水平数，正交表并非唯一。数学家们已经构造出大量的标准正交表。在实际应用中，研究者通常无需自己构造，而是可以借助专业的统计软件（如 SPSSAU 的【正交实验】功能）直接生成。软件会根据用户输入的因素和水平数量，自动匹配最合适的标准正交表，极大降低了使用门槛。

SPSSAU正交表生成软件操作如下：

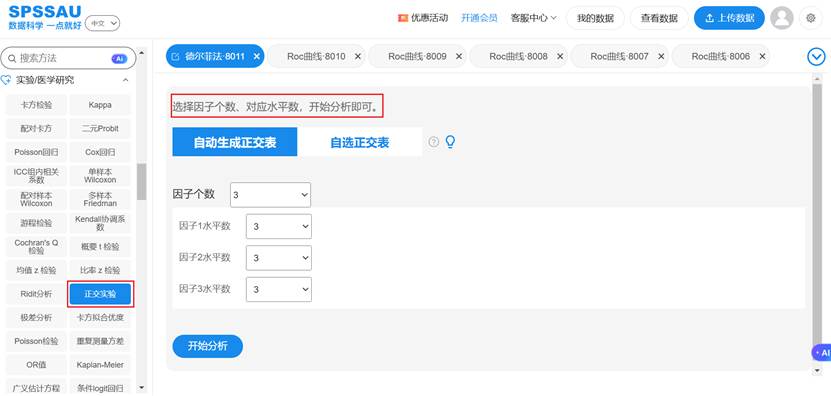
当遇到非标准情况（如各因素水平数不等）时，还可以采用拟水平法、组合法、并列法等对标准表进行改造，展现了正交试验设计体系的灵活性。

三、极差分析

在通过正交表完成少量实验并获得数据后，首要任务是从中提取有价值的信息。极差分析法（又称直观分析法）是最常用、最直观的首选工具。它的核心思想是将每个因素不同水平导致的效应差异进行量化比较。SPSSAU极差分析软件操作如下：

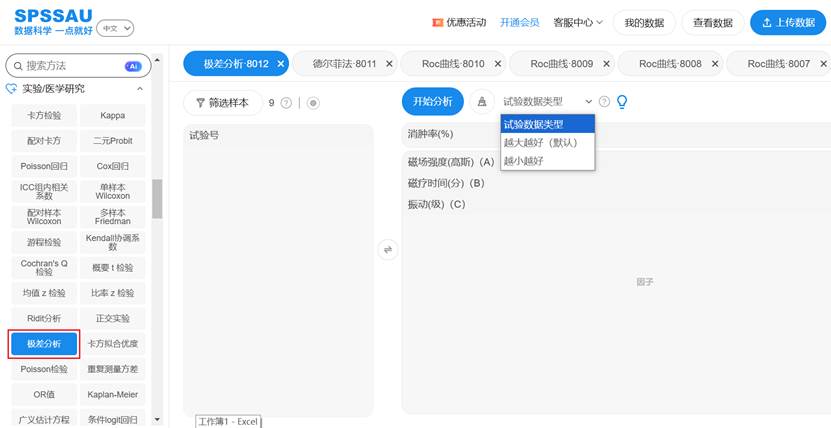
1、极差分析的核心计算

极差分析通常生成一个包含以下关键指标的结果表：

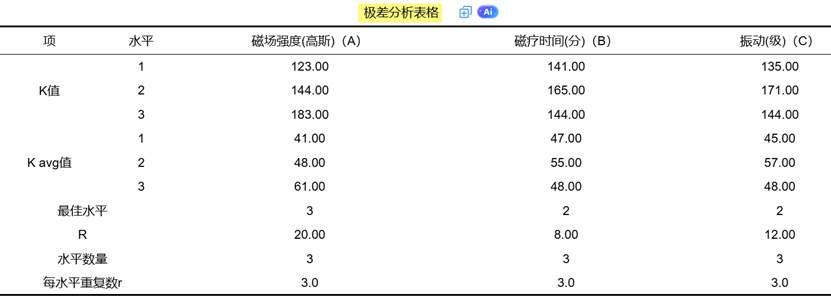
• K值（水平数据和）： 某因素取同一水平时，所有对应实验结果的总和。它反映了在该水平下，所有实验结果的累积效应。
• k值（水平数据均值）： 即 K 值除以该水平出现的次数。这是剔除了实验次数影响后的纯水平效应，是直接比较不同水平优劣的核心指标。对于希望结果“越大越好”（如产量、强度）的指标，k值最大的水平通常为最优水平；对于希望“越小越好”（如杂质含量、磨损率）的指标，则反之。
• 极差（R值）： 某因素所有k值中的最大值与最小值之差。这是极差分析中最具诊断意义的指标。

2、极差R的理论意义

它衡量了该因素对实验结果影响力的大小。 极差越大，说明该因素的不同水平切换时，实验结果的变化幅度越大，即该因素是一个“敏感”因素、主要矛盾。反之，极差越小，则说明该因素水平的变化对结果影响甚微，是一个次要因素或不敏感因素。通过比较各因素的极差R，我们可以清晰地对所有考察因素进行主次排序，从而抓住问题的关键。

3、极差分析的优势与局限性

极差分析法的魅力在于其简洁性与直观性。它无需复杂的统计假设，计算简单，结果一目了然——一张表、一张图（如各因素水平均值趋势图）就能清晰地指出最优组合和因素主次。

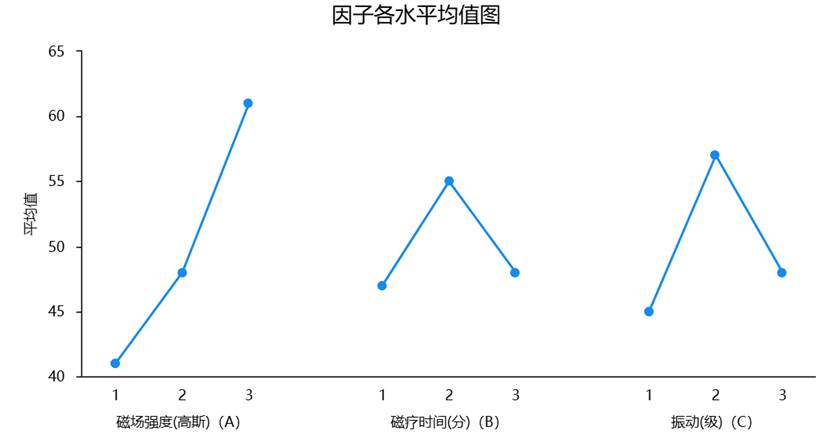
然而，极差分析也有其局限性。它本质上是一种描述性分析，虽然能告诉我们因素影响的大小和顺序，但无法回答一个关键问题：这种影响是真实的系统效应，还是可能由随机误差（实验波动）引起的？ 换言之，它缺乏一个统计学的“显著性检验”。当一个因素的极差看起来“有点大”但又不是特别大时，我们难以做出果断判断。这就需要引入更强大的工具——方差分析。

四、方差分析：为结论加上“统计保险”

方差分析是建立在数理统计基础上，对正交试验结果进行深入分析的标准方法。它超越了极差分析的描述层面，进入了统计推断的领域。

方差分析的核心思想是分解总变异。它将所有实验结果的总波动（总离差平方和），分解为两大部分：

1. 由各因素水平变化引起的波动（因素效应）。
2. 由随机误差引起的波动（误差效应）。

通过比较这两部分波动的大小，来判断因素效应是否显著大于随机误差。

F检验：统计显著性的判决书

方差分析输出的核心是 F值 及其对应的 p值。

• F值：其本质是“因素的均方”（因素效应方差）与“误差的均方”（随机误差方差）的比值。F值越大，说明该因素造成的系统波动远大于随机噪音，该因素的影响就越“突出”。
• p值：这是在原假设（“该因素无影响”）成立的前提下，观察到当前甚至更大F值的概率。通常，我们设定一个显著性水平（如α=0.05）。若p值小于0.05，我们就有足够的统计证据拒绝原假设，认为该因素的影响是“统计显著”的。 这个结论带有概率保证，而非仅仅基于直观感觉。

极差分析与方差分析的对比与协作

我们可以将二者的关系类比于临床诊断：

• 极差分析 如同 “量体温、测血压” 。它能快速发现异常指标（极差大的因素），指出大概的问题所在（最优水平），操作简单，即时可得。但它不能确诊疾病（不能断定影响是否真实存在）。
• 方差分析 如同 “拍CT、做活检” 。它过程更复杂，但能提供确凿的病理证据（p值），明确告诉你异常是否具有统计学意义，精确判断病情的严重程度（各因素的贡献率）。

在实践中，二者并非互斥，而是优势互补、分阶段协作的关系：

1. 初步探索阶段：优先使用极差分析，快速绘制出“影响地形图”，识别出主要因素和潜在最优区。
2. 精确验证与决策阶段：对极差分析找出的关键因素，使用方差分析进行显著性检验。特别是当实验存在不可忽略的随机误差，或需要对优化结论的可靠性进行严格论证（如在学术论文或关键工艺认定中）时，方差分析是不可或缺的。

现代数据分析平台（如 SPSSAU）已将这两种分析流程无缝集成。用户在完成正交实验数据录入后，可以轻松地一键完成极差分析，查看直观的图表结果；同时也可以直接进行方差分析，获得包含F值、p值的详细统计报表。这种集成化操作使得研究者能自由地在“快速扫描”和“深度诊断”两种模式间切换，极大地提升了从实验设计到结论产出的整体效率与科学性。