熵值法与层次分析法：两种常用权重计算方法的原理、流程与应用全解析

综合评价体系中，权重的确定始终是最关键的环节之一。熵值法与层次分析法（AHP）分别代表“客观赋权”与“主观赋权”，两者广泛用于学术研究、政务规划、指数构建、区域评价及工程管理。

一、熵值法：基于信息量的客观权重计算方法

熵值法（Entropy Weight Method）来自信息论。它认为：数据差异越大，信息量越大，指标越重要；数据差异越小，指标越不重要。换句话说，一个指标在各评价对象之间差距很明显，那么它就更有“区分能力”，权重自然更高。

1. 熵值法的核心原理（通过一段话讲清）

熵值法基于信息熵的思想。信息熵原本衡量系统“混乱程度”，但在评价中，它反过来衡量指标“区分能力”。当某指标在不同地区（或企业、个人）中的变动极小，这说明它不能有效区分对象，携带的信息量很低，熵值则高；而变动越大说明信息量越高，熵值越低。熵值法就是通过“1 - 熵值”得到指标的有效信息量，并以此确定权重。因此，熵值法不需要专家参与，权重随数据波动自动调整。

2. 熵值法的计算步骤流程图

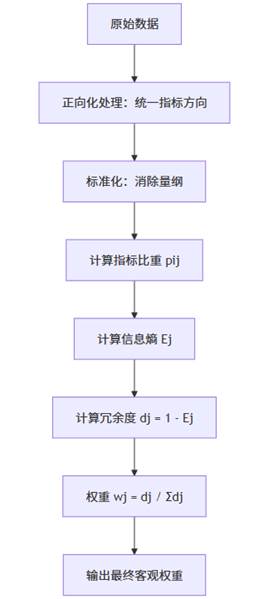
熵值法的计算步骤从数据标准化开始。由于不同指标通常具有不同的量纲和方向（比如“越大越好”的指标，例如收入水平，和“越小越好”的指标，例如污染水平），在计算前必须对所有指标进行无量纲化转换，使其可比。

熵值法计算公式如下：

• 完成标准化后，需要计算各指标在样本中的比例，这一比例反映了各样本在该指标上的相对贡献，是熵值法后续计算的输入。
• 基于比例值，就可以计算指标的熵值。熵值的数学形式源于信息熵公式，将各比例乘以其对数项并求和，最终得到熵值。熵值越大，表示指标的差异越小；熵值越小，说明指标变异度越大。
• 为了让指标的区分能力在权重中体现，熵值法进一步计算“差异度”或称“冗余度”（1−熵值），它代表指标携带的有用信息量，熵值越小则冗余度越大。
• 有了冗余度之后，各指标权重便可通过其冗余度占总冗余度的比例得出。这个过程其实就是一种带有逻辑解释的“归一化”。

3. 熵值法适用场景

熵值法适用于：

• 数据差异本身具有研究意义，例如区域经济差异
• 指标数量较多，人工判断困难
• 评价需要“客观、可重复、无人工干预”

例如绿色发展指数、城市竞争力指数、环境质量评价等，都是典型应用。

二、层次分析法 AHP：让专家和逻辑决定权重的主观方法

层次分析法 AHP 是一种“结构化判断方法”。它强调：复杂决策问题可以拆分成层次，通过两两比较确定相对重要性。其核心在于，将抽象判断转化为数学结果，同时保持判断逻辑的一致性。

1. AHP 的思想原理

AHP 认为复杂决策可以分解成多个层次：目标层 → 准则层 → 指标层。专家不直接给权重，而是使用 1–9 的标度体系，两两比较指标的重要性，例如“指标 A 比指标 B 重要 3 倍”。这些定性的判断构建成判断矩阵。矩阵经过特征值计算后得到权重，同时通过一致性检验确保判断不矛盾。其优势在于逻辑性强、可解释性好，尤其适合需要专家参与的场景，如政策评估、战略决策、风险管理等。

2. AHP 的计算步骤流程图

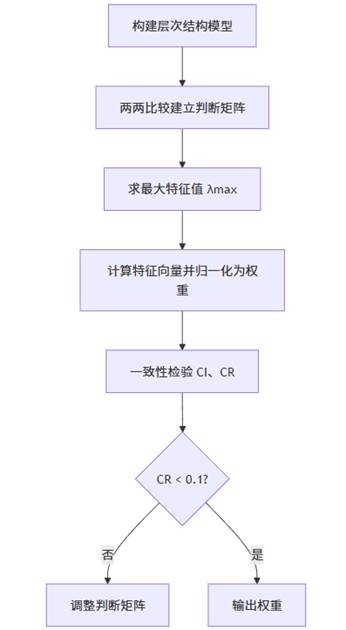
• AHP 的第一步是构建层次结构模型。在实际评价中，复杂的问题往往包含多个目标与子目标。
• 第二步是构建两两比较判断矩阵。AHP 的核心机制并不是直接给出绝对权重，而是通过对任意两个指标进行比较，判断哪一个更重要、重要程度有多强。
• 在判断矩阵构建完毕后，需要通过线性代数方法计算权重。AHP 的权重不是简单求平均，而是通过矩阵的最大特征值及其对应的特征向量来推导。
• 为了确保专家判断是逻辑一致的，AHP 引入了一致性检验。一般 CR 小于 0.1 即认为可接受。

3. 判断矩阵

AHP 使用的 1–9 标度法例如：

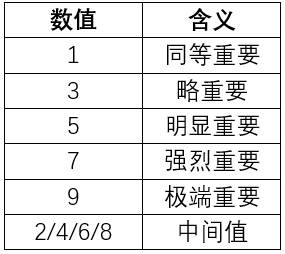
萨蒂提出的 1–9 比例法，将判断等级划分为从“同等重要”到“极端重要”的九个等级，这样专家可以根据经验与专业判断，逐对比较每个指标的重要程度。比较结果形成一个正互反矩阵，即若 A 相对于 B 的重要性是 3，那么 B 相对于 A 的重要性就是 1/3。

4. AHP 的公式核心

AHP层次分析法包括和积法和方根法两类计算方法：

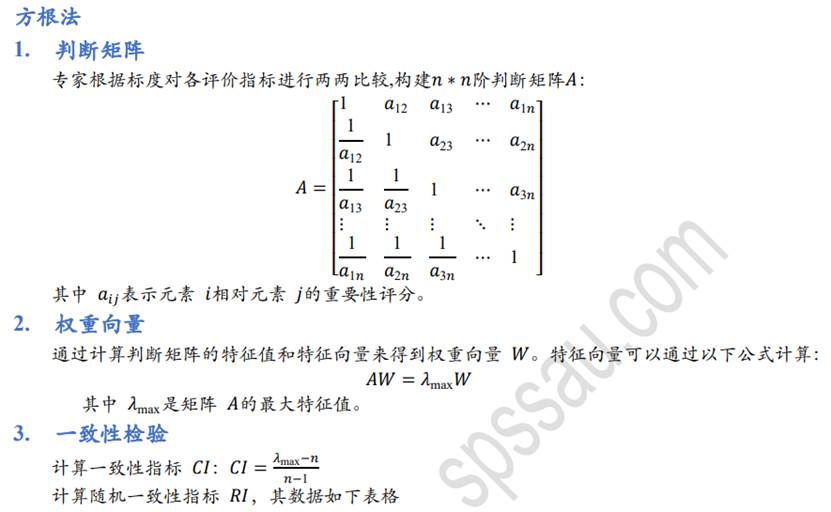
完整版计算公式可查看SPSSAU帮助手册提供的算法公式。

三、客观与主观赋权的差异

熵值法与 AHP 两者代表了权重体系两种完全不同的哲学路径。熵值法认为指标的重要性应由数据内部变异度决定，因而数据差异越大，指标贡献越高。AHP 则认为专家能对指标重要性做更合理判断，因此权重应由人而非数据导向。这两种思想并不矛盾，而是适用于不同的研究目标和数据条件。

在实际应用中，熵值法的优势是客观、透明、可重复。任何人使用同样的数据都会得到同样的权重。它非常适合样本量大、数据充分、指标体系结构稳定的情况。

SPSSAU输出熵值法权重计算结果示例如下：

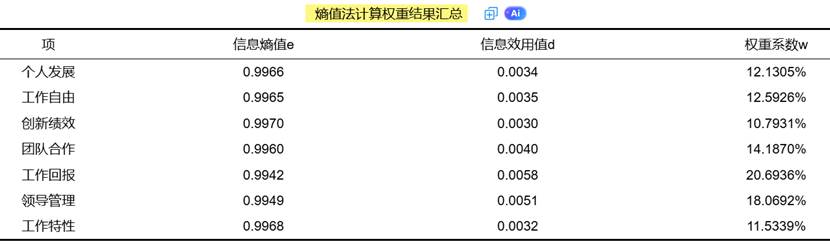
而 AHP 的优势则在于可解释性和灵活性。许多决策类、战略类的评价指标无法依靠数据差异度来决定其重要性。例如衡量城市可持续发展的指标中，“创新能力”和“交通便利度”究竟哪个更重要，本质上是一个政策偏好问题，不是统计变异度能决定的。此时专家判断比纯数据更有解释力。

SPSSAU输出AHP层次分析法结果示例如下：

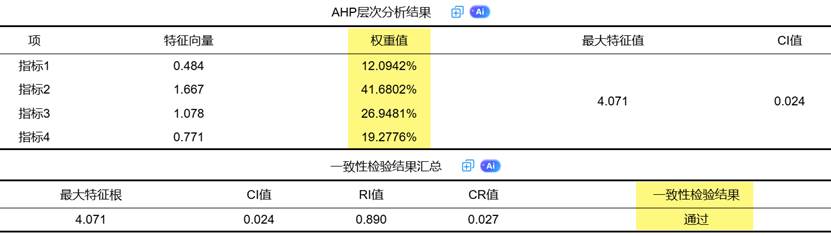
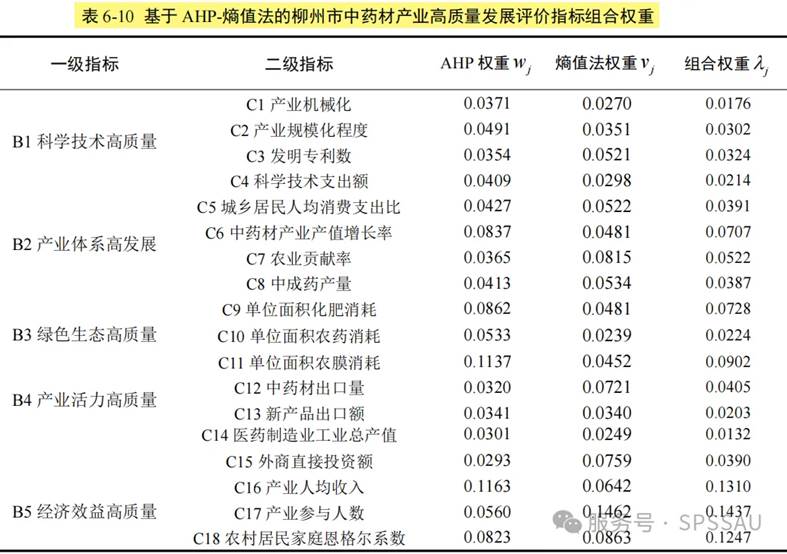
因此，在许多综合评价体系中，研究者常常会选择将两者结合。例如可以先用 AHP 确定一级指标的结构性权重，再用熵值法确定二级指标的客观权重，然后通过层次加权组合，构建一种“主客观结合权重体系”。示例如下：