AHP-熵值法组合权重分析：理论与SPSSAU实现

原创于 2025-12-08 11:01:09 发布 · 192 阅读

CC 4.0 BY-SA版权

文章标签：

1 引言：权重分析方法概述

在多指标决策分析中，如何科学地确定各指标权重一直是研究者关注的核心问题。主观赋权法与客观赋权法各有优劣，而将两者结合的组合赋权法能够有效弥补单一方法的局限性。本文将通过SPSSAU分析平台，深入探讨AHP层次分析法与熵值法的理论基础、分析流程及其组合应用。

在决策科学中，权重确定方法主要分为两大类：主观赋权法依赖于专家经验判断，如AHP层次分析法、FAHP模糊层次分析法、优序图法等；客观赋权法基于数据本身变异程度，如熵值法、CRITIC权重、变异系数法等。

2 AHP层次分析法：理论与SPSSAU实现

2.1 AHP方法基本原理

AHP（Analytic Hierarchy Process）层次分析法是由美国运筹学家T.L.Saaty提出的一种系统化、层次化的多准则决策方法。其核心思想是将复杂问题分解为多个层次和因素，通过两两比较的方式确定各因素的相对重要性。

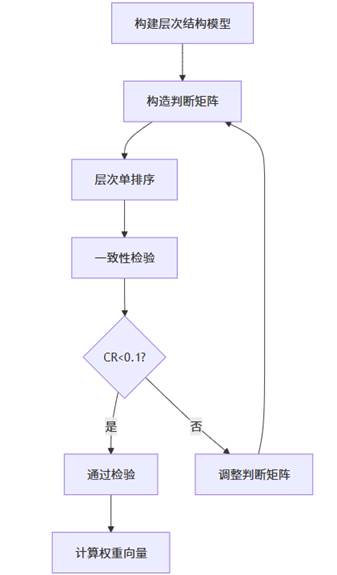
如上图所示，AHP分析流程包括层次结构构建、判断矩阵构造、权重计算和一致性检验四个关键环节。SPSSAU平台自动化地完成了这些复杂计算过程，用户只需输入判断矩阵即可获得专业分析结果。

2.2 AHP核心指标解析

在SPSSAU的AHP分析结果中，包含多个关键指标，每个指标都具有明确的理论意义：

在SPSSAU平台上，这些指标的计算完全自动化，用户无需手动计算复杂的矩阵特征值和特征向量，大大提高了分析效率。

SPSSAU输出AHP层次分析法结果示例如下：

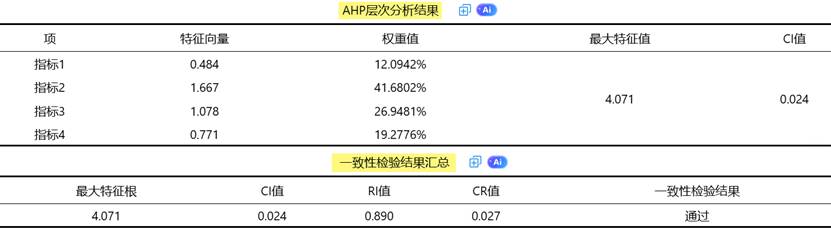
3 熵值法：理论与SPSSAU实现

3.1 熵值法基本原理

熵值法是一种基于信息熵理论的客观赋权方法。在信息论中，熵是衡量系统不确定性的指标，数据离散程度越大，信息熵越小，该指标提供的信息量越大，其权重也应越高。

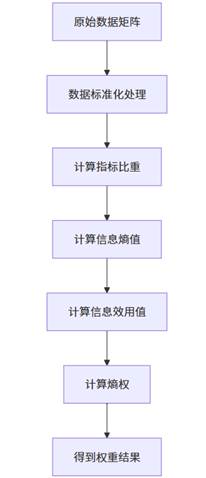
熵值法的计算流程如上图所示，主要包括数据标准化、指标比重计算、熵值计算和权重确定等步骤。SPSSAU平台内置了完整的熵值法计算模块，能够自动完成权重计算。

3.2 熵值法核心指标解析

SPSSAU熵值法分析提供了三个核心指标：

熵值法的核心优势在于其客观性，权重完全由数据本身的特征决定，不受人为主观因素的影响。SPSSAU在计算过程中自动处理了数据标准化、缺失值等问题，确保结果的科学性。SPSSAU输出熵值法计算结果示例如下：

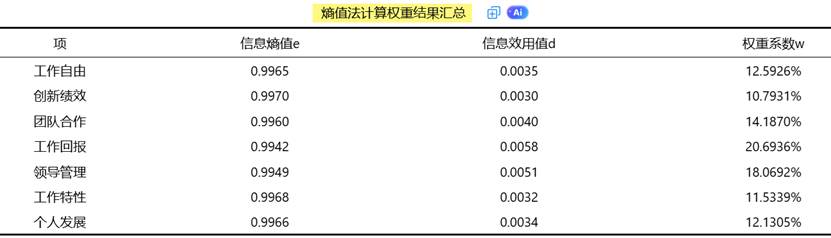
4 AHP-熵值法组合权重分析

组合权重理论框架：单一赋权方法各有局限性，AHP法受主观因素影响较大，而熵值法可能忽视指标的实际重要性。将两者结合的组合赋权法能够兼顾主观经验与客观数据，获得更科学的权重结果。下图为组合权重计算流程图：

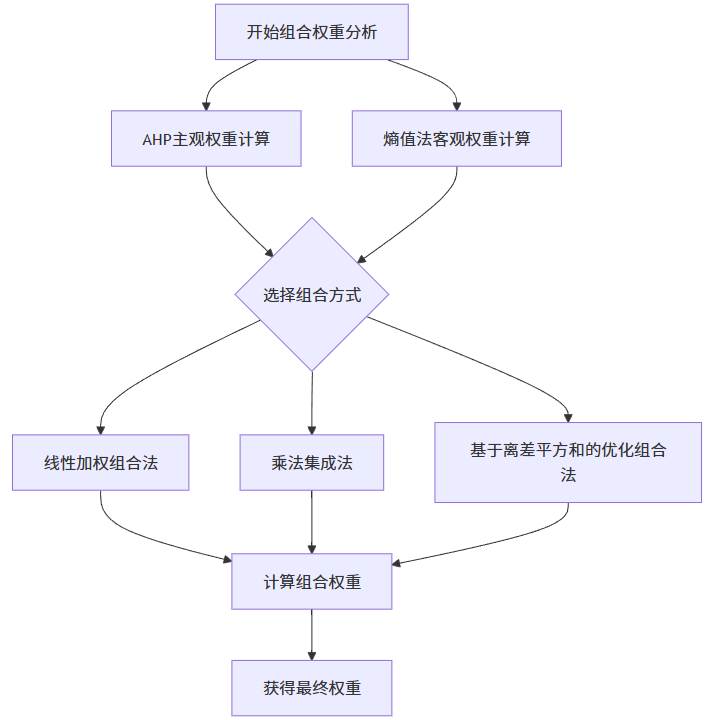
5 组合权重计算方法详解

5.1 线性加权组合法

线性加权是最常用的组合方法，计算公式为：

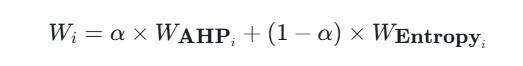
其中，Wi为第i项指标的组合权重，Wahp为AHP法得到的权重，Wentropy为熵值法得到的权重，α为偏好系数(0≤α≤1)。

偏好系数α的确定可以基于专家经验，也可以采用数学优化方法，如基于离差平方和最大化的方法。用户可以根据研究需要调整主客观权重的相对重要性。

5.2 乘法集成法

乘法集成法的计算公式为：

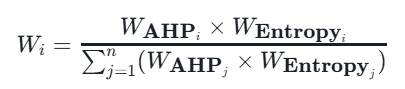
这种方法强调主客观权重的一致性，当某指标在主客观权重中均具有较高值时，其组合权重会进一步增大。

5.3 组合权重的优势

组合权重法综合了主客观赋权的优点：

AHP-熵值法组合权重分析有效整合了主客观信息，是多指标决策分析中较为科学的方法。通过SPSSAU平台，研究者可以轻松实现这一复杂分析过程，无需关注繁琐的计算细节，而将更多精力投入到指标体系的构建和结果解释中。

未来，随着大数据和人工智能技术的发展，权重分析方法将更加智能化。SPSSAU平台也将持续更新算法库，为用户提供更先进、更便捷的分析工具，推动科学研究与决策分析的发展