聚类分析完全解读：理论与SPSSAU实践指南

最新推荐文章于 2025-12-04 22:05:42 发布

原创最新推荐文章于 2025-12-04 22:05:42 发布 · 446 阅读

CC 4.0 BY-SA版权

文章标签：

聚类分析作为探索性数据分析的重要方法，在市场细分、用户画像、生物分类等领域有着广泛应用。它能够根据数据的相似性自动将样本分组，为研究者发现数据内在结构提供有力工具。本文将系统介绍聚类分析的理论框架、核心指标及其在SPSSAU平台上的实现过程。

一、聚类分析的基本原理

聚类分析（Cluster Analysis）是一种典型的无监督学习方法。它不依赖先验标签，而是通过计算样本之间的相似性或距离，将数据自动划分为若干组，使得同组样本内部的差异最小、组间差异最大。在统计学理论中，这种“相似性”可基于数值距离、类别差异或混合特征而定义。SPSSAU 将这一复杂原理转化为一套直观、智能的操作流程：

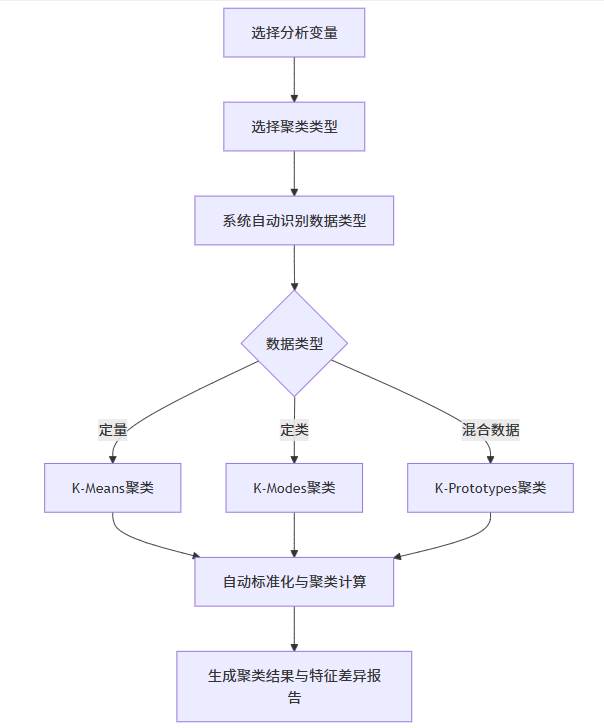
SPSSAU中的智能聚类选择

SPSSAU根据数据类型自动选择合适的聚类算法：

单独定量数据使用 K-Means 聚类；
单独定类数据使用 K-Modes 聚类；
混合型数据使用 K-Prototypes 聚类；
分析前系统可自定义聚类个数，默认自动标准化处理，并保存聚类类别列，便于后续分析。

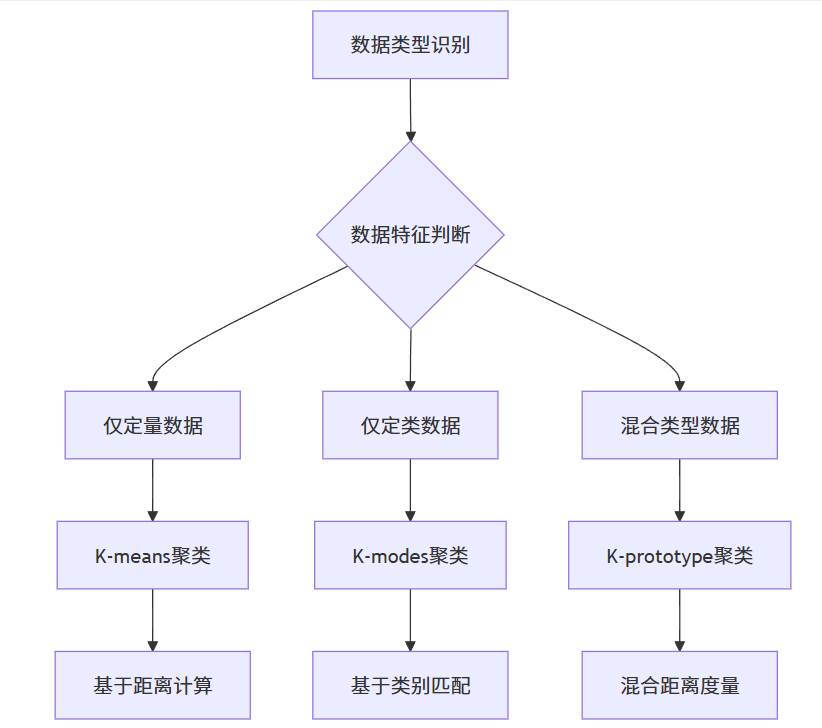
这种智能化算法选择确保了各种数据类型都能获得最合适的聚类处理方案。SPSSAU进行聚类分析页面如下：

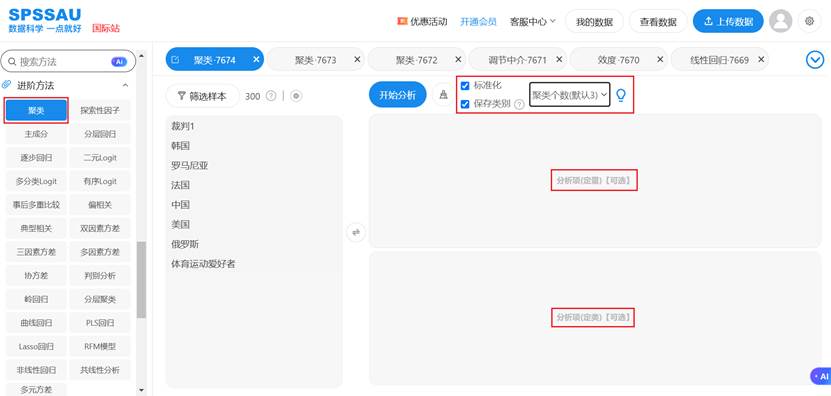
二、聚类分析完整流程

在SPSSAU中进行聚类分析遵循清晰的逻辑流程：

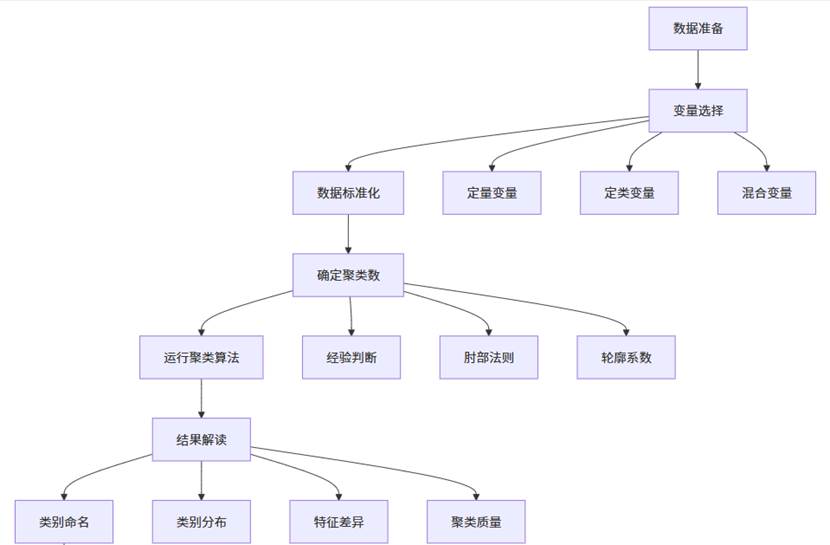
这一完整流程确保了聚类分析的系统性和结果的可解释性。SPSSAU平台将这一复杂过程自动化，用户只需拖拽变量即可获得专业级的聚类分析结果。系统自动完成所有计算与检验，输出图表和文本化分析建议，让研究者既能理解算法逻辑，又能快速形成报告。

三、聚类分析核心指标解析

聚类分析涉及多类统计指标，它们共同构成了完整的聚类效果评估体系。以下是这些指标的系统分类：

1. 聚类基本情况指标

指标类别	具体指标	理论意义
类别分布	频数	每个聚类类别包含的样本数量
	百分比	各类别在总样本中的占比
分布评估	均匀性	各类别样本分布的平衡程度

类别分布指标反映了聚类结果的样本分配情况，理想的聚类应该避免某些类别样本过少或过多。

2. 聚类效果评估指标

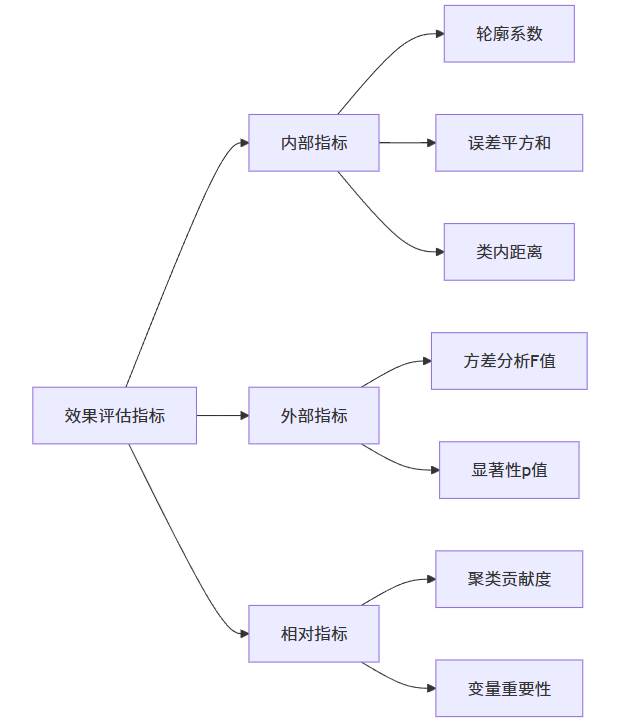
轮廓系数衡量每个样本与自身类别及其他类别的相似程度，取值范围通常为-1到1，值越大表明聚类效果越好。
误差平方和反映各类别内样本的紧密程度，SSE值越小表明类内样本越相似。
方差分析结果通过检验各类别在聚类变量上的差异显著性，验证聚类效果的有效性。

3. 聚类中心指标

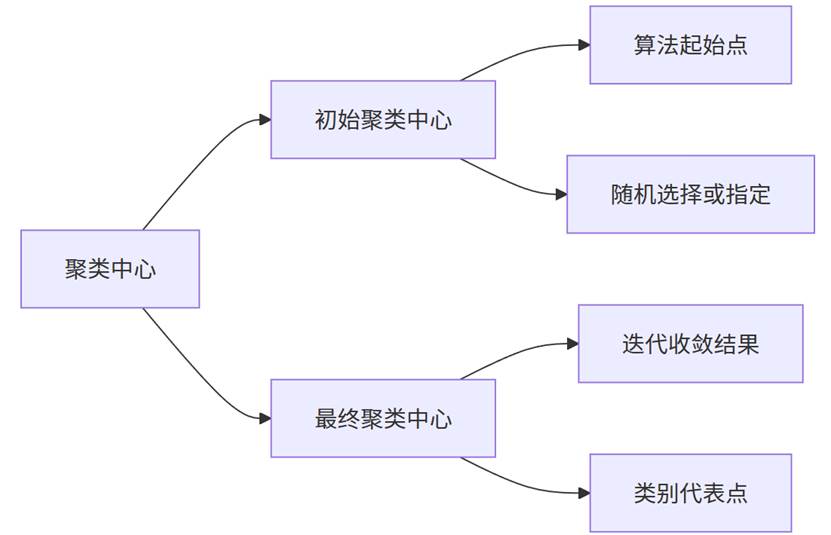
聚类中心是各类别的代表性点，反映了该类别的典型特征。在K-means聚类中，聚类中心是各类别样本的均值点。

4. 变量贡献度指标

聚类贡献度通过图形化方式展示各变量对聚类形成的贡献大小，帮助识别关键区分变量。

四、SPSSAU分析结果表格介绍

1、聚类类别基本情况汇总：结果的“第一层含义”

“聚类类别基本情况汇总”是最直观的结果呈现表。它显示了各个聚类类别的数量和占比，用以描述分群结构是否平衡。说明如下：

若各群体比例相对接近，说明聚类划分较为均衡；
若极度不平衡，可能意味着聚类数过多或变量贡献偏单；
每个聚类代表一类“同质化”的个体群体，是后续差异分析与特征命名的基础。

SPSSAU系统自动生成聚类类别（Cluster_1、Cluster_2……），并在数据表中新增“聚类类别”变量列，方便在后续交叉分析或回归模型中直接使用。

2、差分析差异对比：揭示“为什么不同”

聚类之后，SPSSAU 会自动进行“聚类类别方差分析差异对比”，通过比较不同群体在各个变量上的均值差异，判断每个群体的显著特征。

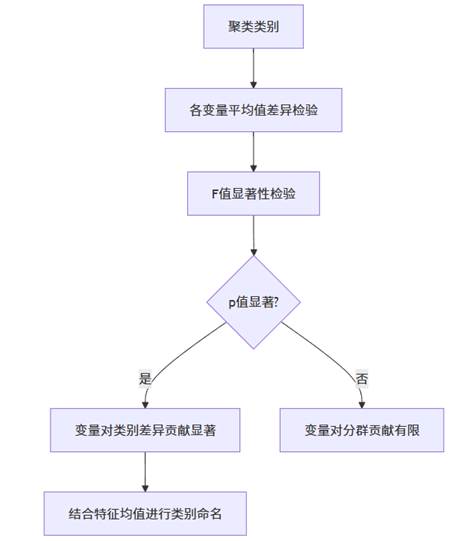
F值（方差比）：用于判断不同类别的平均值是否存在显著差异；
p值：显著性检验标准（常以0.05为界），表示群体差异是否具统计意义；
均值差异：反映每个类别的核心特征，可用于命名或解释聚类。

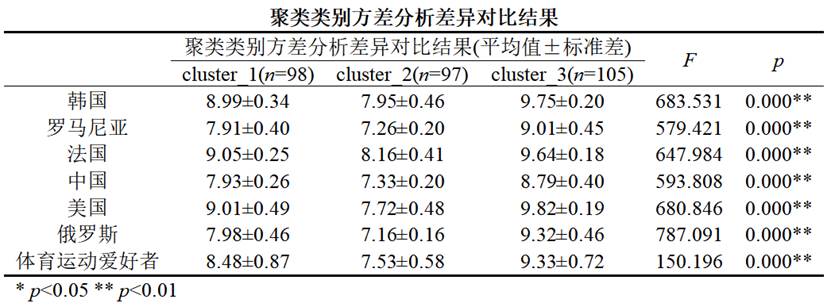
在SPSSAU中，系统智能判断所有研究项的显著性，并提示是否需要对变量进行重新筛选或聚类优化。方差分析是聚类解释的“放大镜”，帮助研究者理解每个类别的特质，进而给出符合语义的群体命名（如“高满意度群体”“理性消费型”“创新导向型”等）。

3、聚类中心表：算法的“数学核心”

聚类中心（Cluster Center）是 K-Means / K-Prototypes 算法的计算核心。它记录了每个类别在各个变量维度上的中心位置，即该群体的“代表点”。

初始聚类中心是算法的起点；
通过迭代更新，系统不断减少误差平方和（SSE），寻找最优分组；
最终聚类中心代表各群体在多维空间中的“质心”，可理解为该群体的典型特征轮廓。

SPSSAU自动输出初始与最终聚类中心值对比，并自动显示误差平方和（SSE）与平均轮廓系数。

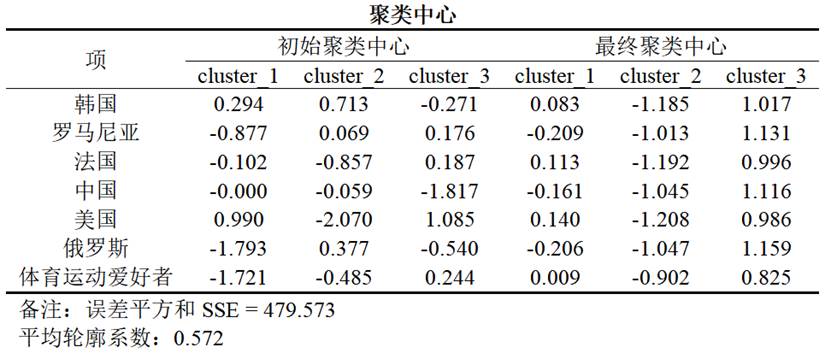
SSE（Sum of Squared Errors）：反映聚类紧密度；
轮廓系数（Silhouette Coefficient）：反映聚类分离度与合理性（越高越理想）。

4、聚类贡献分析：找出“最有价值的变量”

SPSSAU 还会在结果中给出“聚类贡献可视化”，展示各变量对聚类形成的影响程度。

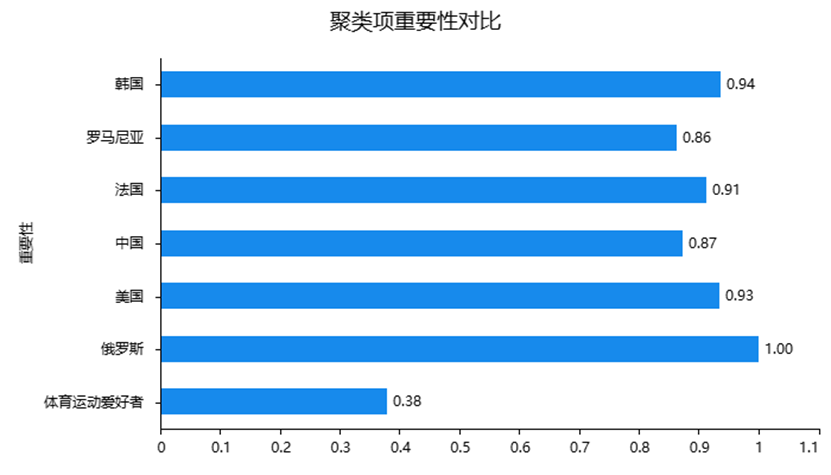
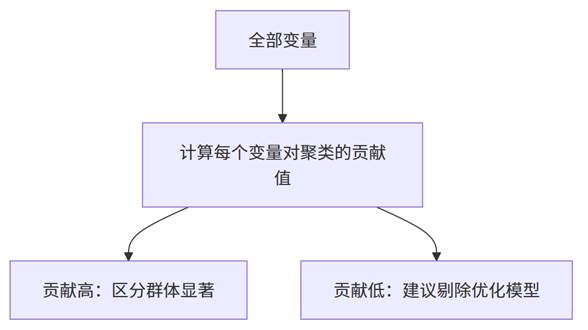
变量贡献越高，说明其在不同群体间差异越大，是区分类别的关键维度；
贡献极低的变量则可能对分群结果无意义，甚至产生噪声；
研究者可根据该结果在SPSSAU中重新选择分析变量，以获得更稳定的聚类结构。

五、SPSSAU 的智能化优势

SPSSAU 聚类模块不仅提供算法，更注重“结果的解释性”与“研究者思维的连贯性”。

1. 一键识别数据类型：无需手动选择算法，系统自动识别变量类型（定量/定类/混合），匹配最优算法。

2. 自动标准化与保存聚类结果：为避免尺度差异影响结果，SPSSAU 默认对定量数据进行标准化处理，同时自动保存“聚类类别”变量，方便继续做交叉分析、回归或判别分析。

3. 智能输出报告：报告自动包含类别分布与比例、差异显著性表、聚类中心变化、变量贡献图、可直接引用的智能结论。

聚类分析作为探索数据内在结构的重要方法，为研究者提供了发现数据自然分组的有力工具。通过本文的系统介绍，我们可以看到，一个规范的聚类分析涉及变量选择、数据预处理、算法选择、结果验证和业务解读等多个环节，每个环节都有其特定的方法学要求。

在实践应用中，研究者应当综合考虑统计指标和业务意义，既要关注聚类质量的数学度量，也要重视聚类结果的业务可解释性和应用价值。SPSSAU平台提供的多角度验证和可视化展示，为这一综合评估提供了有力支持。