空间杜宾模型（SDM）入门与实战：从理论到SPSSAU分析全解析

原创于 2025-12-04 10:14:49 发布 · 476 阅读

CC 4.0 BY-SA版权

文章标签：

空间杜宾模型（Spatial Durbin Model, SDM）是现代空间计量经济学中一颗璀璨的明珠。它以其模型的包容性和解释力的丰富性，在区域经济学、环境科学、公共卫生等众多领域占据了核心地位。对于研究者而言，理解SDM不仅意味着掌握一种先进的统计工具，更意味着获得了一把解开变量间复杂空间互动关系的钥匙。

本文将从理论出发，系统剖析空间杜宾模型的构成、估计、检验与解读框架，并展示如何借助SPSSAU这一智能化分析平台，将复杂的理论转化为清晰、可执行的分析流程。

一、空间杜宾模型（SDM）的理论内核

在传统回归分析中，一个基本假设是样本之间相互独立。然而，“地理学第一定律”指出：任何事物都是相互关联的，距离越近的事物关联性越强。忽视这种空间依赖性，会导致模型估计偏误和结论失真。

空间杜宾模型通过一个优雅的数学公式，将这种空间依赖关系内化于模型之中：

y = ρWy + Xβ + WXθ + ε

这个公式是SDM的灵魂，让我们逐一拆解：

y：我们所关心的因变量（如犯罪率、GDP增长率等）。
X：自变量矩阵，代表可能影响y的一系列因素。
W：空间权重矩阵，这是整个空间计量模型的基石，它量化了不同空间单元之间的“邻近”关系。SPSSAU支持多种构建方式（如邻接、距离反比等），并自动完成行标准化处理，为后续分析奠定基础。
ρWy：因变量的空间滞后项。系数 ρ 衡量了邻近地区的因变量值对本地区因变量的影响，即“溢出效应”或“模仿效应”。例如，周边城市的繁荣是否会带动本城市的发展？
Xβ：自变量的常规影响，与传统回归中的系数意义一致，表示本地自变量对本地因变量的直接影响。
WXθ：自变量的空间滞后项。这是SDM模型最具特色的部分。系数 θ 衡量了邻近地区的自变量对本地区因变量的影响。例如，周边地区的教育投入是否会影响本地的劳动力素质进而影响经济增长？
ε：随机误差项。

SDM的“包容性”体现在它嵌套了其他两种经典空间模型：当 θ = 0 时，SDM退化为空间滞后模型（SLM）；当 θ + ρβ = 0 时，SDM退化为空间误差模型（SEM）。因此，SDM提供了一个更为一般的分析框架，能有效避免因模型设定错误带来的偏误。

二、 SDM分析的核心流程与SPSSAU实现

一个完整的SDM分析包含一系列严谨的步骤。SPSSAU将这些步骤集成在一个清晰的流程中，极大地简化了用户的操作。

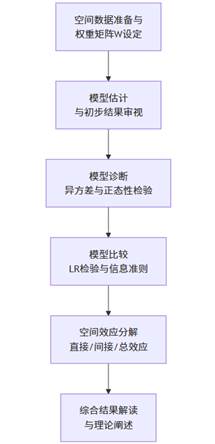
该流程涵盖了从数据准备到最终解读的全过程，确保了分析的严谨性与完整性。SPSSAU平台正是依循此逻辑结构呈现分析结果，引导用户完成整个建模过程。

1. 模型基本参数：分析的基石

任何严谨的空间计量分析报告，首先必须明确模型的基本设定。这部分信息通常以“模型基本参数”表格呈现。

这张表格明确告知读者：本研究使用的是何种模型（如SDM）、样本量大小、空间权重矩阵的定义与标准化方式、以及采用的参数估计方法（如极大似然估计ML）。这些设定直接决定了模型的理论基础和估计结果的有效性。SPSSAU在分析伊始就清晰罗列这些参数，体现了其专业性与规范性。

2. 模型分析结果：回归系数的初步审视

这是模型输出的核心部分，以“空间杜宾SDM模型分析结果”表格呈现，详细列出了每个变量的回归系数、标准误、z统计量、p值和置信区间。

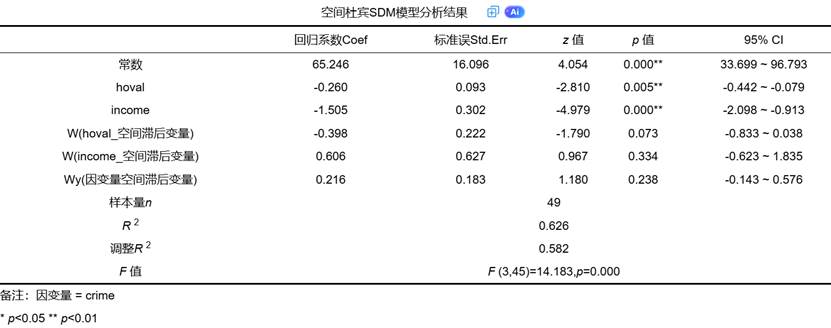
此表格提供了模型参数的初步估计结果。然而，在SDM模型中，绝不能简单地仅凭表中的回归系数（β和θ）来直接解释自变量对因变量的影响。原因是模型包含了Wy和WX项，导致任何一个自变量的变化都会通过空间反馈机制影响其他单元，这使得点估计的“回归系数”无法准确代表其最终的平均影响。该表格的首要作用是进行变量的显著性判断，即通过p值初步筛选出哪些本地效应和空间滞后效应是统计显著的。SPSSAU在此通常会提供智能分析文字，辅助用户进行初步的显著性筛选。

3. 空间效应分解：SDM的真正价值所在

为了克服回归系数解释的局限性，LeSage和Pace (2009) 提出了空间效应分解，这是SDM模型解读的精华，通常以“空间效应”表格呈现。

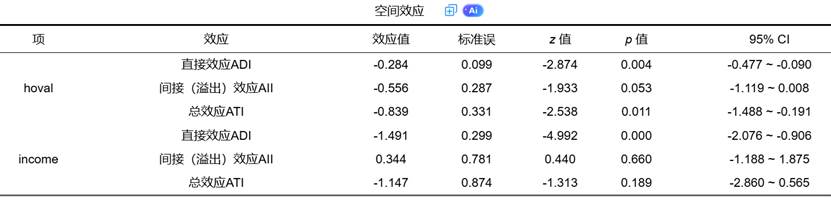
该表格将每个自变量的影响分解为三个部分：

直接效应：衡量某一区域的自变量发生变化时，对该区域自身因变量的平均影响。
间接效应（溢出效应）：衡量某一区域的自变量发生变化时，对所有其他区域因变量的平均影响。这是空间分析中最受关注的部分，它量化了空间互动的强度与方向。
总效应：直接效应与间接效应之和，代表某一区域自变量变化对整个系统内因变量的总体影响。

这才是SDM模型最终结论的依据。 研究者需要根据此表格来判断一个变量的影响是局部的还是全局的，是正向溢出还是负向溢出。SPSSAU自动完成这种复杂的计算和显著性检验，为用户提供了直接可用于论文写作的效应估计值。

4. 模型诊断与比较：确保模型的可靠性

一个优秀的分析不仅要给出结果，还要证明所选用模型是恰当的、可靠的。这部分包括“相关检验汇总”和“LR检验”等表格。

Breusch-Pagan检验：用于检验模型是否存在异方差性。如果存在异方差，标准误的估计可能不准确，此时需要考虑使用稳健标准误等方法进行修正。
Jarque-Bera检验：用于检验模型残差是否服从正态分布。在极大似然估计法下，残差的正态性是保证统计推断有效的重要前提。

LR检验（似然比检验）：用于进行模型选择。它通过比较SDM模型与其简化模型（SLM或SEM）的似然函数值，来判断SDM这个更复杂的模型是否必要。如果检验结果不显著，则意味着简化模型可能已经足够。

信息准则（AIC, SC等）：另一种模型选择工具。当不同模型之间无法通过LR检验清晰区分时，信息准则提供了一个判据：通常认为AIC或SC值较小的模型更优。

SPSSAU将这些检验汇集于一处，方便用户全方位地评估模型质量，并为选择SDM模型而非其他空间模型提供统计依据。

三、为什么选择SPSSAU进行空间杜宾模型分析？

面对如此复杂的模型理论和高维的矩阵运算，手工实现的难度极高。SPSSAU的出现，极大地降低了空间计量分析的门槛。操作示例如下：

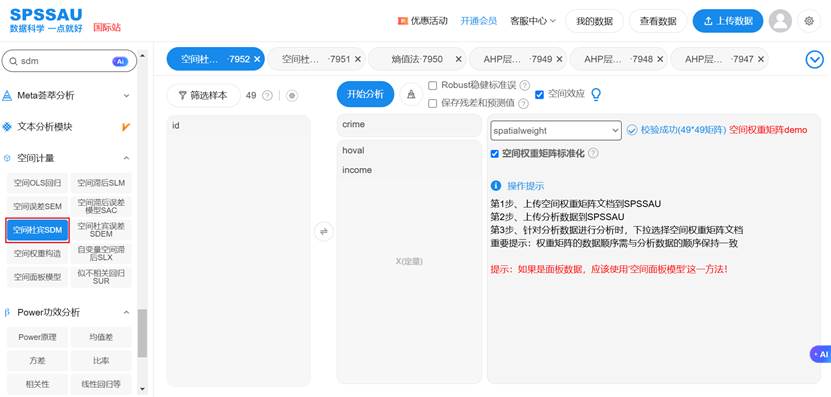
“一站式”流程设计：SPSSAU的分析界面严格遵循上图所示的分析流程，从权重矩阵上传到最终效应分解，引导用户一步到位完成全部分析，无需在不同软件或编程环境间切换。
自动化与智能化：用户只需关注数据与模型设定，SPSSAU在后台自动完成所有复杂的矩阵运算、迭代估计和统计检验。其内置的“智能分析”功能，能对关键结果进行文字描述，帮助初学者快速抓住重点。
结果的规范性与出版级标准：SPSSAU输出的所有表格均符合学术期刊的规范格式，且专业术语准确。无论是效应分解表还是检验统计量，都可直接用于研究报告和学术论文的撰写。
强大的模型比较能力：平台内置了LR检验和信息准则，方便用户在SDM、SLM、SEM等不同空间模型之间进行科学的比较和选择，确保最终使用的模型是最优的。

四、总结

空间杜宾模型（SDM）通过引入因变量和自变量的空间滞后项，为我们提供了一个强大而灵活的分析框架，以揭示变量间复杂的空间依赖结构。掌握SDM，意味着需要深入理解从其基本参数设定、回归系数初步判断，到关键的空间效应分解，再到一系列严谨的模型诊断与比较的完整逻辑链。