德尔菲法理论知识、软件操作教程与指标解读

在复杂决策、政策制定或前瞻预测中，我们常常面临这样的困境：单一专家意见可能偏颇，群体讨论又容易受权威或从众心理影响。有没有一种方法，既能汇集多方智慧，又能避免群体决策的常见陷阱？

答案是肯定的。德尔菲法，这套起源于上世纪 50 年代的专家咨询方法，历经半个多世纪的迭代与验证，已成为战略研究、指标构建、技术预测等领域不可或缺的工具。它不追求开会时的“热烈讨论”，而是通过一套严谨的匿名、迭代、反馈的控制性流程，让专家智慧在静默中沉淀、收敛，最终达成可靠共识。

一、德尔菲法：不止是“反复发问卷”

德尔菲法的命名源于古希腊的阿波罗神庙遗址“德尔菲”，寓意着“预知未来”。其核心并非简单地多次向专家发放问卷，而是一套结构化、匿名的群体沟通流程。它旨在克服传统专家会议中存在的身份、地位、表达能力和群体压力所带来的偏差。

经典德尔菲法通常包含以下几个关键特征：

1. 匿名性： 专家之间互不见面、不知彼此身份，所有意见均通过协调方（研究者）中转。这有效消除了权威效应和从众压力，鼓励专家独立、自由地表达真实观点，即使是少数或非主流意见也能得到呈现。
2. 迭代性与可控反馈： 过程包含多轮（通常为2-4轮）问卷。每一轮结束后，研究者会将上一轮的统计分析结果（如均值、四分位距、争议点）匿名汇总后，作为下一轮问卷的反馈材料发给每位专家。专家可以参照群体意见的分布，重新考虑并修改自己之前的判断。
3. 统计化的群体响应： 最终结果不是某个权威的结论，而是以统计指标（如中位数、四分位数区间）的形式，呈现专家群体意见的集中趋势与离散程度。这使结论更具科学性和透明性。
4. 寻求共识，但也包容分歧： 其目标是通过迭代促使意见收敛，但最终报告也会清晰展示未达成共识的领域，为决策者提供更全面的图景——知道“大家一致同意什么”与“大家为何争论”同等重要。

这种方法论上的设计，使得德尔菲法特别适用于解决非结构化问题、预测长期趋势、构建评价指标体系以及评估政策可行性等场景。

二、共识的度量：核心统计指标的理论解读

在德尔菲法的多轮迭代中，研究者需要通过一系列统计指标来量化专家意见的“集中程度”与“协调程度”，并以此作为筛选指标和判断是否终止调查的依据。理解这些指标背后的统计学意义，是正确解读德尔菲结果的关键。

下面，我们通过一个典型的德尔菲法分析流程概览图，来建立整体的认知框架：

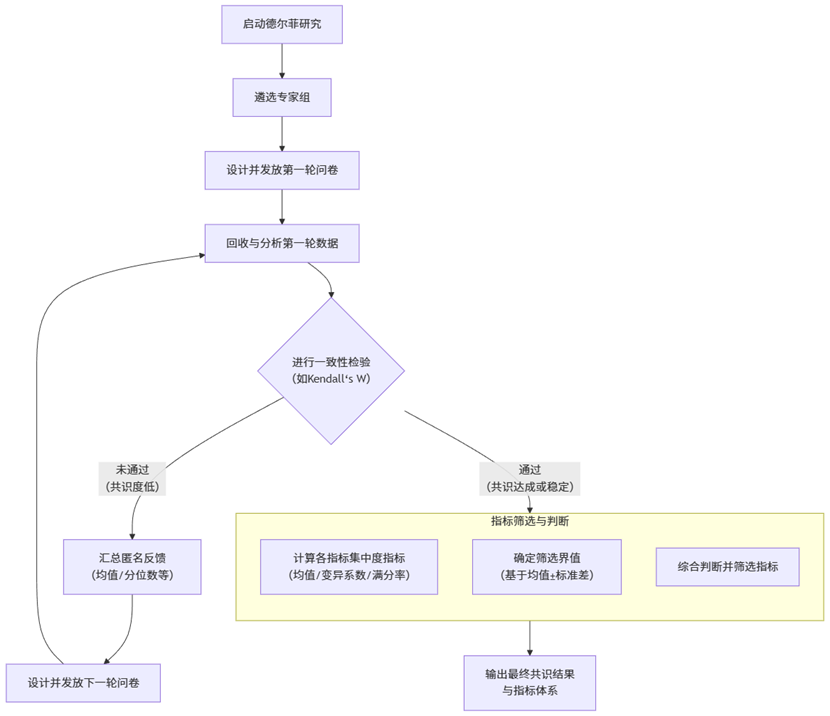
如图所示，一套完整的德尔菲分析遵循着“收集意见 → 检验共识 → 反馈修正 → 筛选确定”的闭环流程。其中，统计检验与指标筛选是承上启下的核心环节。接下来，我们深入解读这些核心指标。

1. 意见一致性检验：Kendall 和谐系数

在每一轮或最终轮结束后，我们需要判断专家们的打分是否存在统计上显著的一致性，即他们的评价是否“协调”。Kendall 和谐系数 正是用于衡量多个评定者对多个被评对象评价一致性的非参数统计量。SPSSAU德尔菲法分析结果示例如下：

它将所有专家对所有指标的打分转换为等级序次，通过比较专家之间所赋等级的一致程度来计算系数W。W的取值范围在0到1之间。

W = 0： 意味着专家们的评价完全不一致，等级排序是随机的。

W = 1： 意味着专家们的评价完全一致，对所有指标的优劣排序完全相同。

 通常认为W > 0.5即表示一致性较好。但更重要的是，需要伴随卡方检验。若检验的p值小于显著性水平（如0.05），则拒绝“评价无关”的原假设，认为专家意见具有显著的一致性。反之，即使W值看起来尚可，若p值不显著，也不能断定达成了统计意义上的共识。

2. 意见集中程度指标：三大筛选标尺

当意见趋于一致后，我们需要对每一个被评价的“指标”（如政策条款、技术项目、风险因素）进行筛选，判断其是否应被纳入最终体系。主要依赖三个维度的统计量，SPSSAU输出结果示例如下：

• 算术平均值： 这是最直观的集中趋势度量，代表专家群体对该指标重要性或可行性的平均看法。理论意义在于，它反映了指标的“绝对接受度”。平均值越高，说明该指标被认为越重要或越可行。
• 变异系数： 计算公式为标准差除以平均值。它是一个消除量纲的相对离散度指标。理论意义在于，它反映了专家群体对该指标看法的分歧程度。CV值越小，说明专家意见越集中，共识度越高；反之，则说明即使平均值可能不低，但专家间存在较大争议。
• 满分频率： 指给予该指标最高分（满分）的专家所占的百分比。理论意义在于，它从另一个侧面反映了指标的“卓越认可度”。一个指标可能平均分中等，但若有一部分专家坚决认为其极其重要（打满分），那么该指标可能具有关键性或特殊性，值得关注。

3. 筛选界值的确定：基于群体基准的动态门槛

仅仅计算每个指标的均值、CV和满分率还不够，我们需要一个客观的“门槛”来决定取舍。德尔菲法中常采用的方法是：利用本轮所有指标这三个统计量各自的平均值和标准差来构建“界值”。

• 计算方法： 例如，对于“算术平均值”，其筛选界值通常设定为 “所有指标平均值的均值 - 所有指标平均值的标准差”。对于“变异系数”，界值则为 “所有指标CV的均值 + 所有指标CV的标准差”。
• 理论逻辑： 这种方法本质上是基于本轮专家评价的整体分布特征，设定一个相对标准。它将那些明显偏离群体共识中心的指标（即重要性偏低、争议性过大或获得高度认可比例过低的指标）识别出来。这种动态界值法比设定一个固定数值（如“均值必须大于4”）更为科学和灵活，能适应不同研究的具体情况。

三、从数据到决策：现代工具如何赋能德尔菲分析

传统的德尔菲法涉及大量的数据整理、计算和图表绘制工作，过程繁琐且易错。如今，专业的统计分析平台（如 SPSSAU）已经将这一套流程进行了高度集成化和自动化，极大地提升了研究的效率和规范性。SPSSAU操作示例如下：

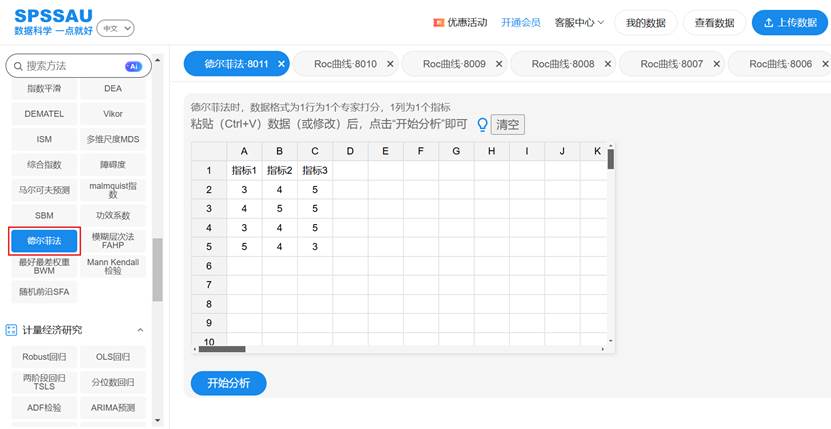
以一次典型的分析流程为例，现代工具通常提供：

1. 一站式分析模块： 研究者只需将多轮专家打分数据按格式录入，平台即可自动完成所有核心计算，包括Kendall和谐系数检验、各项集中程度指标计算、动态界值生成等。
2. 可视化的共识诊断： 自动生成如箱线图来展示每个指标得分的分布情况。箱线图能直观呈现中位数、四分位距和潜在异常值，让研究者一目了然地看出哪些指标共识度高（箱子短），哪些存在极端意见（异常点）。

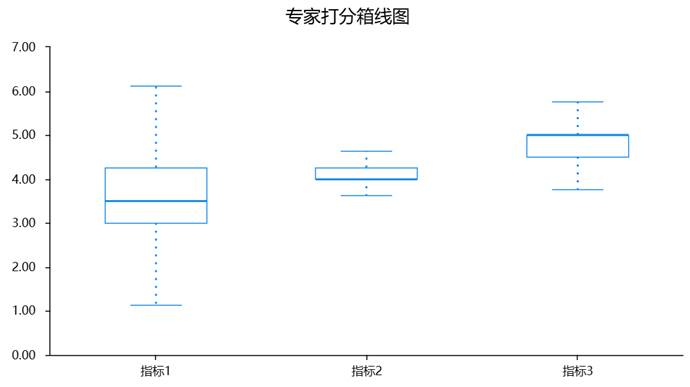
1. 智能的筛选判断： 系统会根据预先设定的界值规则（如上述的“均值-标准差”规则），自动对每个指标进行“通过/不通过”的判断，并给出“综合判断”建议，减少了人工比对和误判的可能。
2. 详细的引导与解释： 好的平台（如SPSSAU）不仅输出表格和图形，还会对每一个输出结果提供通俗易懂的“分析建议”，解释指标含义、判断标准和实际研究意义，如同一位随时在线的统计顾问，这对于非统计学背景的研究者尤为友好。

通过将复杂的统计过程封装在简洁的操作界面之后，工具让研究者能更专注于研究设计、专家遴选和结果诠释等更具创造性的环节，真正实现了“技术为人服务”。

四、优势、局限与适用边界

德尔菲法并非万能钥匙，清晰认识其优劣是正确使用它的前提。

主要优势：

• 汇集智慧，避免干扰： 有效提取了独立专家意见的精髓。
• 过程可控，结论透明： 多轮反馈和统计输出使过程可追溯，结论基于数据。
• 适用性广： 尤其适用于数据缺失、理论不足、需要前瞻判断的复杂问题。

内在局限与挑战：

• 对专家质量的极度依赖： “垃圾进，垃圾出”。专家的选择直接决定了结果的质量。
• 耗时耗力： 多轮问卷的发放、回收、整理和分析周期较长。
• 可能抑制真正的创新： 趋向共识的过程可能会磨平那些超前、反直觉却可能是真正突破的少数派观点。
• 统计共识不等于真理： 最终达成的一致意见，也可能是一种集体误判。

因此，德尔菲法最适合的应用场景是探索性、预测性和评估性研究，其产出更适宜作为高级别的决策参考依据，而非不容置疑的最终结论。它常常与其他研究方法（如文献分析、案例分析、AHP层次分析法）结合使用，以相互印证和补充。

结语

德尔菲法，本质上是一套将主观专家判断进行客观化、结构化处理的方法论体系。它不迷信单一权威，也不陷入群体喧嚣，而是在匿名与反馈、独立与互动、发散与收敛之间，精心设计了一条通往相对可靠共识的道路。

当这种方法与像 SPSSAU 这样高效、智能的数据分析工具相结合时，研究者便能如虎添翼，将更多精力从繁琐的计算中解放出来，投入到更深刻的问题洞察与战略思考中去。