面板数据协整检验：理论与操作全解析

一、什么是面板数据与协整关系？

面板数据（Panel Data）是指在一段时间内对多个个体（如国家、企业、家庭等）进行重复观测所得到的数据集。它同时包含了时间维度和截面维度，因而能够更好地捕捉个体异质性与动态行为。

然而，面板数据中许多经济变量虽然本身是非平稳的（即具有单位根），但它们之间可能存在长期均衡关系——这就是协整（Cointegration） 的概念。简单来说，如果两个或多个非平稳序列的线性组合是平稳的，我们就称这些序列之间存在协整关系。

例如，居民消费与收入、汇率与物价、多个国家的GDP增长率等，都可能存在这种长期稳定关系。协整检验正是为了判断这种关系是否真实存在。

二、为什么要在面板数据中做协整检验？

在时间序列分析中，如果直接对非平稳序列进行回归，容易产生“伪回归”问题，即模型虽然拟合度高，但实际没有经济意义。协整检验的出现正是为了解决这一问题。

而在面板数据中，由于数据维度更丰富、样本量更大，协整检验不仅能提升估计效率，还能控制个体异质性，更准确地识别变量间的长期关系。因此，面板协整已成为现代计量经济学中不可或缺的分析工具。

三、面板协整检验的常用方法

目前最常用的面板协整检验方法主要有两类：

1. Engle-Granger 两步法

• 第一步：对变量进行回归，得到残差；
• 第二步：对残差进行单位根检验，若平稳则认为存在协整关系。

这种方法简单直观，但缺点是不能处理多个协整向量的情况。

2. Johansen 协整检验

Johansen方法是基于向量自回归模型的似然比检验，能够判断出协整关系的个数，适用于多变量系统。其原假设从“不存在协整关系”开始，逐步检验“最多存在一个协整关系”“最多两个”等，直到无法拒绝原假设为止。

在实际研究中，Johansen方法更为常用，尤其是当变量个数多于两个时。

下面我们通过一个Mermaid流程图来展示面板协整检验的整体分析流程：

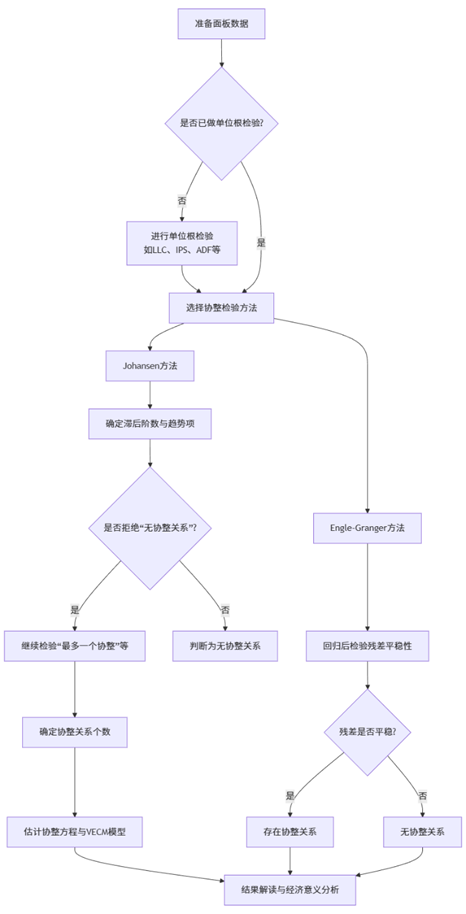
流程图解读：该图展示了面板数据协整检验的完整分析路径。从数据准备开始，需先进行单位根检验确认变量的平稳性，随后选择协整方法。若使用Johansen法，需确定滞后阶数与趋势项形式，并逐步检验协整关系的个数；若使用EG两步法，则需检验回归残差的平稳性。最后，根据检验结果估计模型并解读经济含义。

四、SPSSAU中的协整检验实战：以Johansen方法为例

在实际操作中，如何快速、准确地完成协整检验？这里我们以SPSSAU平台为例，展示其协整检验模块的操作与输出解读。

SPSSAU提供了Johansen协整检验和Engle-Granger协整检验两种方法，并支持自动定阶、多种趋势设定等功能，非常适合初学者和研究者使用。操作示例如下：

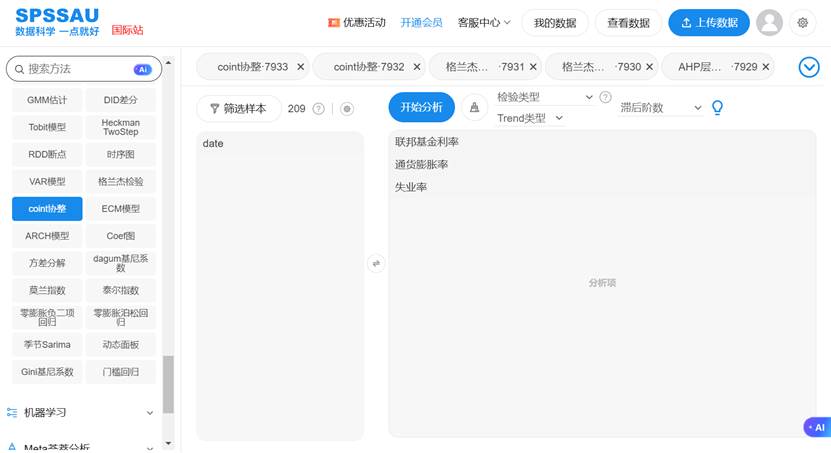
4.1 参数设置

以下是SPSSAU中一次典型的Johansen协整检验参数设置：

• 检验类型：Johansen法适用于多变量系统，能判断协整关系个数。
• 滞后阶数：SPSSAU支持自动定阶，基于VAR模型的AIC、BIC等准则选择最优滞后阶数。
• Trend类型：根据序列趋势选择“常数c”“线性趋势”或“None”。

4.2 自动定阶过程

SPSSAU在后台会基于信息准则（AIC、BIC、FPE、HQIC）自动选择最优滞后阶数。以下是本次示例的定阶结果：

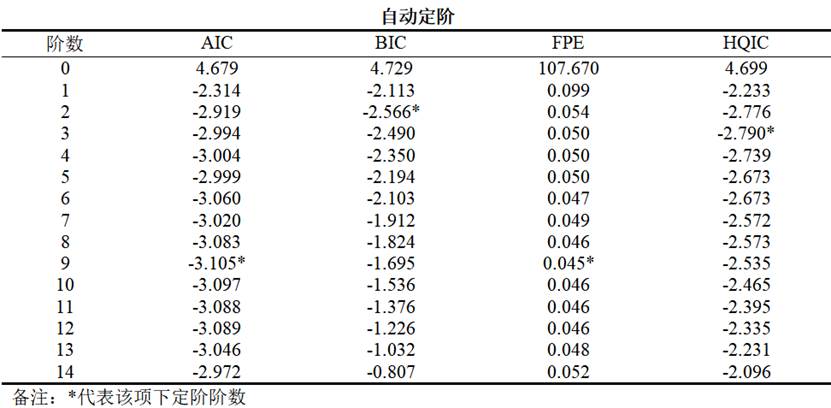
系统最终选择滞后1阶，是基于四个准则的最小值减1的原则，确保模型既简洁又有效。

4.3 Johansen协整检验结果

SPSSAU输出两个统计量结果：迹统计量（Trace） 和最大特征根统计量（Max-Eigen）：

结果表明：

• 在1%水平上拒绝“无协整关系”，说明至少存在一个协整关系；
• 在1%水平上拒绝“最多1个协整”，说明至少存在两个协整关系；
• 在5%水平上不拒绝“最多2个协整”，说明系统中存在2个协整关系。

最大特征根统计量也支持这一结论。

4.4 结果解读与经济意义

协整关系的存在意味着这些非平稳变量之间存在长期稳定关系。我们可以进一步建立向量误差修正模型（VECM） 来分析短期波动与长期均衡之间的互动机制。

五、面板协整检验的注意事项

1. 数据预处理：务必先进行单位根检验，确认变量为同阶单整。
2. 模型设定：合理选择趋势项与滞后阶数，避免模型设定错误。
3. 小样本问题：面板数据若时间维度较短，检验功效可能下降。
4. 软件选择：推荐使用SPSSAU等集成化平台，其自动定阶与智能解读功能能大幅提升分析效率。

六、总结

面板协整检验是识别变量间长期关系的重要工具。本文从理论基础出发，结合SPSSAU实战案例，系统介绍了协整检验的流程与方法。无论是学术研究还是商业分析，掌握这一方法都将为你的数据分析能力加分。

如果你正在寻找一个操作简便、输出清晰的协整分析工具，不妨试试SPSSAU——它不仅能自动完成阶数选择、趋势判断等复杂步骤，还提供智能分析与结果解读，让你专注于模型背后的经济逻辑。