空间杜宾误差模型（SDEM）详解，从理论到SPSSAU分析全流程

最新推荐文章于 2025-12-04 10:16:18 发布

原创最新推荐文章于 2025-12-04 10:16:18 发布 · 613 阅读

CC 4.0 BY-SA版权

文章标签：

在空间计量模型的选择中，研究者常常面临一个核心权衡：是关注于变量间实质性的空间互动（如溢出效应），还是优先处理由遗漏变量等导致的误差项空间依赖性？空间杜宾模型（SDM）与空间误差模型（SEM）分别给出了侧重点不同的解答。然而，当理论预期自变量的空间溢出是研究的核心，同时又需要控制误差项中可能存在的空间相关性以保障推断的稳健性时，一个将二者优势结合的混合模型便展现出其独特价值——这便是空间杜宾误差模型（SDEM）。

一、 SDEM模型的理论内核：为何需要这种混合设定？

SDEM模型的核心思想在于，它将两种不同来源的空间依赖性进行了清晰的划分和同时的建模：

外生的自变量空间溢出：这是研究者关心的结构性效应。它直接刻画了一个地区的自变量如何影响其他地区的因变量，例如邻近地区的教育投入对本地区人力资本的正向外溢。
误差项的空间自相关：这是需要控制的干扰性效应。它源于模型未观测到的、且具有空间相关性的因素（如共同的文化氛围、相似的治理水平），如果忽略，会导致标准误估计有偏，影响统计推断的可靠性。

SDEM模型的数学形式精准地反映了这一“效应分离”的思想：

y = Xβ + WXθ + u, u = λWu + ε

让我们解析其核心构成：

y = Xβ + WXθ + u：这部分与自变量空间滞后模型（SLX） 完全一致。
- Xβ 代表了本地自变量对本地因变量的直接影响。
- WXθ 是模型的精华，代表了外生的空间溢出效应，系数 θ 直接度量了其强度与方向。
u = λWu + ε：这部分与空间误差模型（SEM） 完全一致。
- 它表明随机误差项 u 本身存在空间自回归结构，由 λWu 刻画，λ 是空间误差系数。
- ε 是服从经典假设的随机扰动项。

SDEM与SDM的关键区别在于，SDEM不包含因变量的空间滞后项 Wy。这意味着它不假设因变量之间存在直接的、内生的相互影响（如模仿效应、竞争效应）。其理论定位可以通过下图清晰地展现：

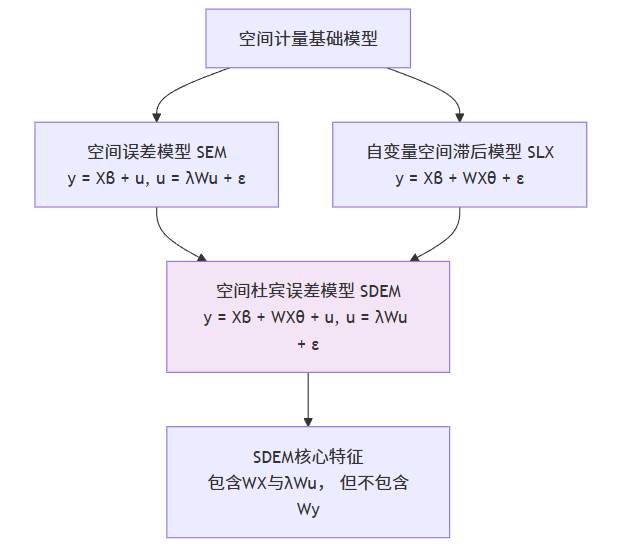
SDEM可以视为SLX模型与SEM模型的直接结合体。它继承了SLX模型对外生空间溢出（WX）的关注，同时吸收了SEM模型对误差项空间依赖性（λWu）的控制能力，但明确排除了因变量的内生交互效应（Wy）。

二、 SDEM模型的分析框架与SPSSAU输出解读

在SPSSAU中执行SDEM分析，会得到一套结构化的输出。理解每一部分的理论含义，是正确应用该模型的关键。

1. 模型基本参数表

此表格是分析报告的起点，确保了研究的透明性与可重复性。

它明确宣告了本研究采用的模型是“空间杜宾误差SDEM模型”，并列出了所依据的空间权重矩阵、样本量以及估计方法（如极大似然法ML）。这些信息是同行评估研究设计严谨性的基础。

2. 模型分析结果表：核心参数的估计

这张表格呈现了所有关键参数的估计值。

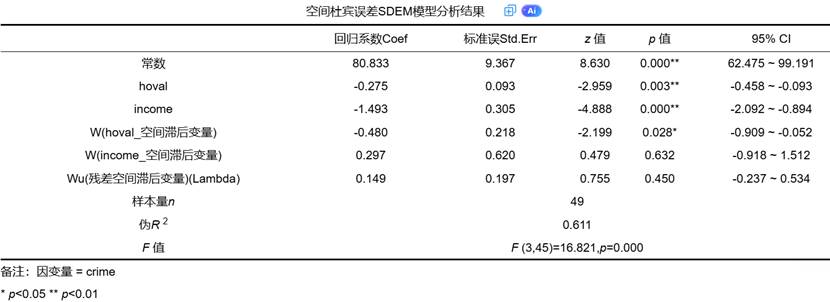
自变量回归系数（β）：反映了在控制了空间溢出和误差依赖后，本地自变量对本地因变量的直接影响。
自变量空间滞后项系数（WX, θ）：直接度量了外生的空间溢出效应。这是研究者关注的核心参数，一个显著的 θ 为研究假设提供了直接证据。
空间误差系数（Lambda, λ）：衡量了误差项空间依赖的强度。一个显著的 λ 说明控制此类依赖性是十分必要的；反之，如其不显著，则意味着数据中这种干扰性效应可能很弱。
重要提示：由于SDEM模型不包含 Wy，其回归系数 β 和 θ 具备直接的可解释性，无需像SDM模型那样进行复杂的空间效应分解来理解其含义。β 可近似视为直接效应，θ 可近似视为间接效应。

3. 空间效应分析表：效应的直观呈现

尽管SDEM的系数已相对直观，SPSSAU仍会输出一张“空间效应分析”表格。

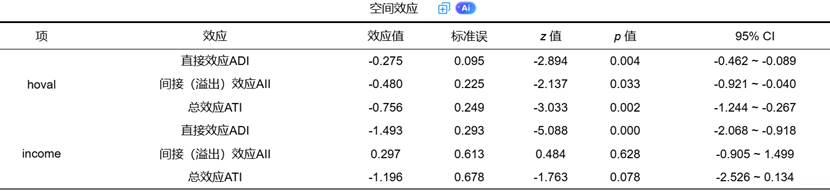
在SDEM框架下，由于没有 Wy 引入的反馈回路，空间效应的计算变得直接。该表格通常直接基于回归系数 β 和 θ 进行计算和报告：

直接效应 非常接近于 β。
间接（溢出）效应 非常接近于 θ。
总效应 为二者之和。

这张表格的作用在于以标准化术语（直接、间接、总效应）呈现结果，便于与SDM等模型的研究结论进行跨研究比较。

4. 模型诊断与比较工具

LR检验（似然比检验）：SPSSAU提供了SDEM与其嵌套模型的比较。例如，检验SDEM是否显著优于SDM（原假设H0: SDEM，即约束 ρ=0）。如果检验结果不显著（p > 0.05），则倾向于选择更简洁的SDEM模型；反之，则可能需要包含 Wy 的SDM模型。

信息准则（AIC, SC）：在模型选择中至关重要。研究者可以分别运行SDEM、SDM、SLX等模型，并通过比较AIC或SC值（通常越小越好）来进行数据驱动的模型择优。

三、何时选择SDEM模型？SPSSAU的实现路径

选择SDEM模型，通常基于以下严谨的考量：

理论驱动：研究假设明确指向外生的空间溢出机制（即 WX 效应），并且从理论上判断，因变量之间的内生互动（Wy 效应）并非研究关注的重点或理论上不显著。
控制稳健性需求：研究者希望在一个更稳健的框架下估计空间溢出效应，通过控制误差项的空间依赖性（λWu），确保 θ 的估计和统计推断是可靠的。
模型比较结果：通过LM检验、LR检验或信息准则的比较，发现SDEM相较于SDM或SLX提供了相似或更好的拟合效果，且模型更为简洁。

SPSSAU为SDEM模型的应用提供了高效且专业的实现路径：

清晰的模型选项：用户在SPSSAU的“空间计量”模块中可直接选择“空间杜宾误差（SDEM）模型”，这使得模型设定意图明确，从源头上保证了分析的针对性。
自动化复杂计算：平台自动完成包含空间误差结构的极大似然估计，并输出包括系数表、效应分解表、检验统计量和信息准则在内的完整结果。
智能分析与比较：其内置的智能分析能自动提示关键参数的显著性，并提供了LR检验等工具，直接帮助用户在SDEM与SDM等竞争模型之间做出科学选择。SPSSAU操作示例如下：

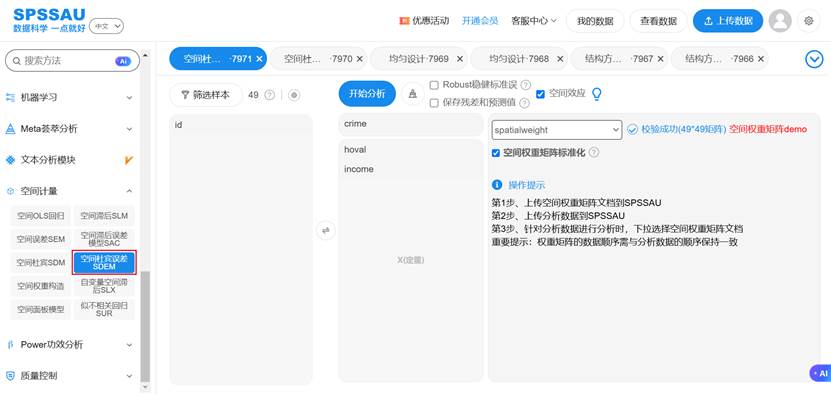
四、总结

空间杜宾误差模型（SDEM）通过巧妙地结合外生空间溢出（WX）与误差项空间依赖（λWu），同时排除了内生交互效应（Wy），为我们提供了一个在理论上有针对性、在估计上稳健的分析框架。它特别适用于那些核心兴趣在于识别自变量空间溢出效应，并致力于保障统计推断可靠性的研究场景。

SPSSAU通过其专业化的分析模块，使得这一具有精细设定的空间计量模型变得易于实现和解读。它赋能研究者能够轻松地驾驭SDEM模型，从复杂的空间数据中，清晰地剥离出结构性的空间溢出效应，同时有效控制潜在的干扰性空间依赖，从而得出更为严谨和可信的研究结论。在实证研究日益讲求机制识别与估计稳健性的今天，SDEM模型及其在SPSSAU中的便捷实现，无疑将成为区域科学、经济学、社会学等领域研究者的又一宝贵分析工具。